Indice
Maglia triangolare
Argomento della lezione
Innanzitutto sono stati chiariti alcuni aspetti riguardo il telaietto rettangolare analizzato nell'ultima lezione di laboratorio(03/03/2016). Punto focale della lezione è stata l’analisi della maglia triangolare: dopo una prima descrizione della struttura, si è utilizzato il manipolatore algebrico Maxima per confrontare la rigidezza della maglia triangolare 3 volte iperstatica(3 incastri interni collegano le 3 travi che costituiscono la struttura) con la rigidezza dell’analoga isostatica(nella quale le 3 travi sono incernierate tra loro); l’analisi è stata condotta sia nel caso di sezione piena che sezione cava.
Richiami al telaietto rettangolare
Prima di passare all'argomento chiave della lezione soffermiamo l’attenzione sulla struttura analizzata nell’ultima lezione di laboratorio (03/03/2016) costituita da un telaietto rettangolare.
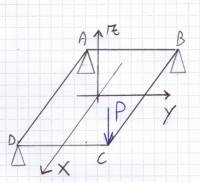
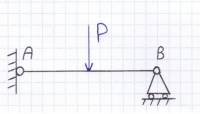
Il telaietto rettangolare era costituito da 3 appoggi nei punti A, B e D, e su di esso agiva un carico verticale P in C; questa struttura non è simmetrica in quanto il sistema di vincoli non è simmetrico: se si opera una sezione in un punto a caso della struttura risultano sei incognite iperstatiche: sforzo normale, due componenti del taglio, due componenti del momento flettente e un momento torcente, che le due facce a cavallo di quella sezione possono trasmettersi reciprocamente; seppur il sistema di partenza non sia simmetrico si vede che analizzando il sistema di carichi, comprensivo di reazioni vincolari e carico P, si ottiene una distribuzione di carichi antisimmetrica rispetto i piani zx e yz(l’antisimmetria non è altro che una forma particolare di simmetria) e ciò ci consente di analizzare un solo quarto della struttura: procedendo in questo modo si passa da sei incognite iperstatiche ad una sola incognita iperstatica e quindi una netta semplificazione dei calcoli.
In realtà esistono sistemi non simmetrici anche notevolmente più semplici, come una trave vincolata con una cerniera e un carrello, caricata da un carico trasverso in mezzeria P, dove si può fare un ragionamento del tutto analogo a quello fatto per il telaietto:
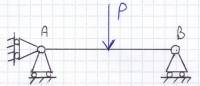
Tecnicamente questo sistema non è simmetrico perché abbiamo da una parte una cerniera e dell’altra un carrello: tuttavia la distribuzione dei carichi e il diagramma del momento flettente sono perfettamente simmetrici e la struttura viene studiata come simmetrica, vediamo perché:
La cerniera è equivalente a due carrelli ad asse ortogonale, e possiamo considerare una struttura del tipo:
Il carrello in A posto ad asse orizzontale, che è l’elemento che violerebbe la simmetria, essendo il sistema isostatico, quindi staticamente determinato (quindi risolubile con sole considerazioni di equilibrio), ed essendo le azioni in direzione orizzontale autoequilibrate(nella fattispecie sono nulle) avrà reazione vincolare nulla(tale risultato consegue da una semplice considerazione di equilibrio alla traslazione orizzontale). Dal momento che il carrello ad asse orizzontale posto in A esplica una reazione vincolare nulla, non perturba le caratteristiche della sollecitazione e quindi non perturba lo stato tensionale e lo stato deformativo della struttura: quindi un vincolo assente e un vincolo che esplica una reazione vincolare nulla sono equivalenti dal punto di vista dello stato di sollecitazione, pur tuttavia non essendo equivalenti dal punto di vista cinematico: se tolgo il carrello ad asse orizzontale il sistema è labile, se lo lascio è invece posizionato nello spazio. Inoltre sempre in virtù del fatto che il carrello ad asse orizzontale esplichi una reazione vincolare nulla io potrei inserirlo in qualunque punto della struttura, senza che sia alterato lo stato di sollecitazione della struttura: il carrello ad asse orizzontale può essere applicato in mezzeria, nel punto A o nel punto B, come in qualsiasi punto arbitrario della struttura.
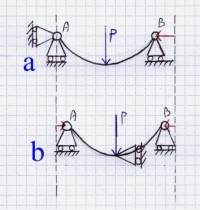
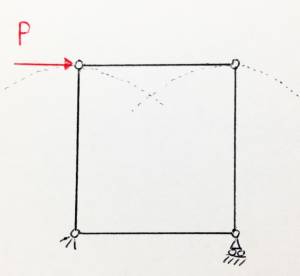
Supponiamo che la forza P applicata in mezzeria sia tale da produrre grosse deformazioni e consideriamo due diverse configurazioni:
a) Carrello ad asse orizzontale posto nel punto A;
b) Carrello ad asse orizzontale posto in mezzeria: con tale configurazione il sistema risulta simmetrico.
Nell’immagine sovrastante, in rosso sono indicati gli spostamenti dei punti A e B rispetto la loro posizione nella struttura indeformata che è riportata con il tratteggio verticale.
a) Nella configurazione (a), affinché siano rispettati vincoli, la struttura avrà una deformata posizionata nello spazio in modo tale che i punti A e B non traslino in direzione verticale, e che il punto A non trasli in direzione orizzontale: se in virtù della curvatura e dei grandi spostamenti la distanza orizzontale tra i punti A e B tende a ridursi, è il carrello in B a spostarsi orizzontalmente e la cerniera in A a rimanere ferma;
b) Nella configurazione (b) con il vincolamento simmetrico, il punto che rimane orizzontalmente fermo è il punto di mezzeria: i punti A e B che rimangono verticalmente fermi in virtù dei carrelli ad asse verticale, traslano orizzontalmente, ciascuno di una quantità pari alla metà di quanto trasli il punto B nella configurazione (a) col punto A fisso: con tale configurazione abbiamo una deformata simmetrica; La differenza tra la deformata nelle due configurazioni analizzate è solo un moto di corpo rigido in direzione orizzontale. Più genericamente possiamo dire che tra le varie configurazioni, ottenute con un diverso posizionamento del carrello ad asse orizzontale, seppur lo stato di sollecitazione non muta, il campo di spostamenti della struttura(deformata) differisce da una configurazione all’altra semplicemente di un campo di moto di corpo rigido.
Quanto detto per la trave, è ciò che è stato fatto per il telaietto rettangolare; nel telaietto avevamo un sistema di vincoli che non era simmetrico, però il sistema era staticamente determinato ossia le reazioni vincolari si potevano trovare per considerazioni di equilibrio; in realtà è meglio fare una distinzione per quel che concerne il telaietto: il sistema è staticamente determinato per quanto riguarda le reazioni vincolari ma non è staticamente determinato per quel che concerne le caratteristiche della sollecitazione: cioè le reazioni vincolari si trovano solo con considerazioni d’equilibrio ma il momento flettente no. Potendo risolvere le reazioni vincolari con sole considerazioni d’equilibrio, noto che nel punto C è applicato il carico P, abbiamo trovato le reazioni vincolari tutte di entità P.
L’aver sostituito i vincoli con le reazioni vincolari ci ha dato la possibilità di utilizzare l’antisimmetria della distribuzione di carichi sulla struttura che semplifica i calcoli, tuttavia abbiamo rilevato che la soluzione ottenuta analizzando ¼ della struttura per antisimmetria non rispetta i vincoli della struttura originaria in termini di spostamenti, pur soddisfando essi in termini di forze; allora la soluzione in termini di spostamenti ottenuta per antisimmetria a partire dal quarto di struttura analizzato è stata corretta con moti di corpo rigido in modo da soddisfare le condizioni cinematiche imposte dai vincoli nella struttura originaria; tale moto di corpo rigido lo possiamo suddividere in:
- Traslazione rigida verso il basso di una quantità pari a δ, spostamento subito dal punto dove è applicata la forza verticale P;
- Rotazione rigida intorno all’asse passante per i punti B e D di una quantità tale che lo spostamento verticale del punto A diventi nullo.
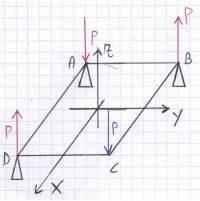
Volendo si può interpretare la cosa in maniera leggermente diversa: se prendiamo la struttura originale caricata dal carico P e con i vincoli posti nei punti A B e D possiamo immaginare una struttura derivata nei quali aggiungo carichi eguali alle reazioni vincolari in ogni singolo punto:
I carichi aggiunti non modificano lo stato di sollecitazione della struttura perché applicati direttamente al vincolo: i carichi P aggiunti in corrispondenza dei vincoli, possono essere sostenuti da due elementi in parallelo: il vincolo e la struttura; la struttura ha rigidezza finita, mentre il vincolo ha rigidezza infinita: con due rigidezze in parallelo, il carico si ripartisce sulla base della rigidezza e avendo in quei punti due elementi in parallelo, uno, il vincolo, infinitamente rigido, e l’altro, la struttura, di rigidezza finita, il carico si scarica tutto sul vincolo e nulla sulla struttura; per cui il sistema di carichi aggiuntivi, dato che sono applicati nei vincoli, non solleciterà la struttura in maniera diversa dal sistema di carichi originario e quindi le caratteristiche della sollecitazione della struttura con il sistema di carichi aggiuntivi, inseriti in corrispondenza dei vincoli non muteranno rispetto alla struttura con il semplice sistema di carichi originari; tuttavia in questo caso rientro perfettamente nella tipologia di sistemi con carichi autoequilibrati nei confronti di traslazione x, y e z e rotazioni intorno a x, y e z, per cui il sistema alla quale abbiamo aggiunto come carichi aggiuntivi, in corrispondenza dei vincoli, proprio le reazioni vincolari dei vincoli, è caratterizzato da reazioni vincolari degli appoggi nulle e quindi nel sistema derivato i tre appoggi in A, B e D sono semplicemente dei posizionamenti e non inseriscono reazioni vincolari nella struttura e quindi possono essere spostati arbitrariamente: una volta aggiunto il sistema di carichi ausiliari, gli appoggi esplicano una reazione vincolare nulla e quindi è lecito pensare di posizionarli poi in maniera arbitraria: la soluzione in termini di spostamenti che ottengo a fronte di un posizionamento arbitrario di quei vincoli è distinta dalla soluzione ottenuta considerando i vincoli della configurazione originaria di un moto di corpo rigido, cioè da un moto al quale sono associate sollecitazioni nulle. Come già detto la soluzione in termini di caratteristiche di sollecitazione, e quindi di stato tensionale e deformativo è indipendente, nel caso di strutture isostatiche, dal posizionamento di vincoli che esplicano reazioni vincolari nelle direzioni in cui i carichi sono autoequilibrati e quindi esplicano reazioni vincolari nulle e quindi sono vincoli solo di posizionamento.
N.B in genere vincoli che esplicano una reazione vincolare diversa da zero sono detti genericamente vincoli, mentre vincoli che esplicano una reazione vincolare nulla sono detti di posizionamento perché danno semplicemente una posizione alla struttura definita e univoca nel caso in cui si desidera una soluzione in termini di spostamenti ben precisa e non solo definita a meno di uno spostamento di corpo rigido.
Maglia triangolare
La maglia triangolare, costituita da tre travi saldate tra loro a formare un triangolo, è l’elemento base di tutte le strutture leggere come bracci di gru da costruzione ( costituiti da reticoli di tralicci di tubi ).
Caratteristiche
I 3 componenti sono tra loro saldati, si utilizza quindi un vincolo di incastro interno che mantiene la continuità di spostamenti e rotazioni; nello spazio è necessario considerare tre spostamenti e tre rotazioni, nel piano due spostamenti e una rotazione.
Sostituendo gli incastri interni con cerniere ( cerniere sferiche nello spazio ) la struttura non diventa labile quindi non viene creato un meccanismo ( è lecito parlare di struttura completamente triangolata nel piano, l’equivalente nello spazio è il tetraedro). Le figure 1 e 2 mostrano la maglia dotata di cerniere interne.
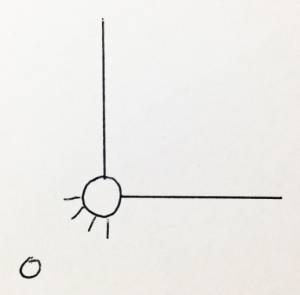
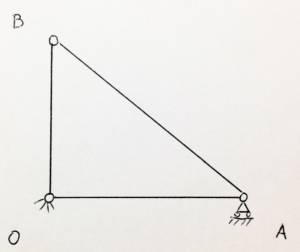
Per questa sua caratteristica la maglia triangolare si distingue dalla maglia quadrilatera che può sopportare carichi solo se i giunti sono saldati, altrimenti siamo in presenza di un parallelogramma articolato ( struttura non completamente triangolata e labile).
Il carico P provoca la deformazione della struttura ed i vincoli non eserciteranno alcuna reazione sulle travi.
Analisi delle cerniere sferiche interne

La sfera viene resa solidale ad uno dei 3 tratti di trave, accoppio gli altri 2 tratti con la cerniera sferica, vedi figura 3: ci sono 3 g.d.l di rotazione per ogni tratto: vengono liberati 6 g.d.l. per ogni cerniera sferica applicata al posto di un incastro.
E’ possibile raffigurare una cerniera sferica anche come in figura 4 ed in tal caso i g.d.l. liberati sono 9 di cui 3 costituiti dalla rotazione della sfera sui 3 assi, rotazioni non considerate nella nostra analisi: si ottiene lo stesso risultato suddetto.

Tipicamente la rigidezza associata al giunto saldato è infinita, approssimazione grossolana soprattutto in presenza di un giunto mal progettato.

La figura 5 evidenzia la perdita di rigidezza della struttura, perdita non considerata supponendo che il giunto saldato abbia rigidezza infinita.
Analisi
La maglia triangolare con giunti saldati è 3 volte iperstatica nel piano, sostituendo agli incastri le cerniere interne la struttura diventa staticamente determinata, molto più semplice da risolvere. Utilizzando cerniere i 3 tratti di trave vengono caricati solo assialmente ( carico normale ) ed essi agiscono come biellette ( ipotesi valida solamente nel caso in cui i carichi esterni siano concentrati sui giunti e non includano momenti flettenti ). L’analisi che andremo a svolgere ha lo scopo di determinare l’errore derivante dalla sostituzione degli incastri con cerniere.
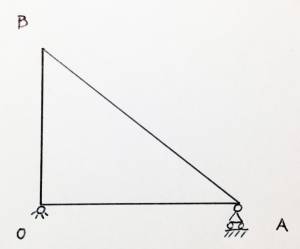
Nel caso in esame abbiamo considerato una maglia triangolare equivalente a quella in figura.
Alla maglia è applicato un carico arbitrario P che induce nella struttura una deformazione valutabile grazie al teorema di Castigliano. Esso dice che lo spostamento, o la rotazione, di un elemento solido elastico è definito dalla derivata parziale dell'energia potenziale elastica espressa in funzione delle forze e dei momenti applicati alla struttura, eseguita rispetto a una di tali forze che sia applicata all'elemento considerato nel punto e nella direzione dello spostamento desiderato. Di conseguenza lo spostamento δ in corrispondenza del punto di applicazione di un generico carico P, nella direzione stessa di P, sarà uguale alla derivata dell'energia potenziale U rispetto a P. L'energia potenziale è definita come: $$ U=\int_{l}(\frac{M_{f,x}^{2}\cdot J_{yy}+M_{f,y}^{2}\cdot J_{xx}+M_{f,x}\cdot M_{f,y}\cdot J_{xy}}{2E(J_{yy}\cdot J_{xx}-J_{xy}^{^{2}})}+\frac{N^{2}}{2 EA}+\frac{\eta_{x}\cdot T_{x}^{2}+\eta_{y}\cdot T_{y}^{2}+\eta_{xy}\cdot T_{x}\cdot T_{y} }{2GA} +\frac{M_{t}^{2}}{2GK_{t}})dl $$
dove η{x,y}=1.11 per sezioni circolari piene, come nel caso in esame.
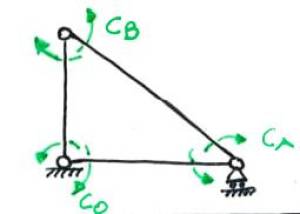
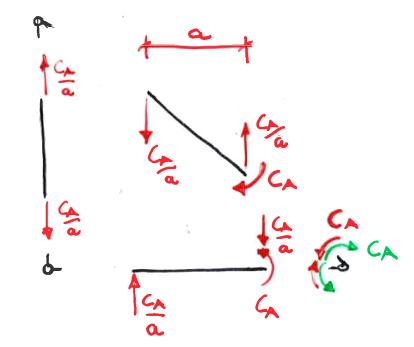
La struttura da noi analizzata è una struttura 3 volte iperstatica. Pertanto per procedere nell'analisi occorre sostituire ai giunti infinitamente rigidi interni dei nodi delle cerniere per poter avere una struttura staticamente determinata. A questo punto alla maglia triangolare isostatica ottenuta, applico le coppie di reazione iperstatiche interne ai nodi come in figura:
La struttura risultante è completamente triangolata, ossia, una volta fatte le precedenti sostituzioni, essa è in equilibrio cinematico, cioè non labile. A questo punto occorre risolvere la struttura, considerando singolarmente il contributo di ciascuna forza (o momento) applicato alla struttura. Poiché si tratta di carichi rappresentati da funzioni lineari sarà poi possibile applicare la sovrapposizione degli effetti di ciascuna azione alla struttura finale: quindi si considerano separatamente i contributi di $P$, $C_{O}$, $C_{A}$ e $C_{B}$.
Effetti del carico $P$ applicato in B
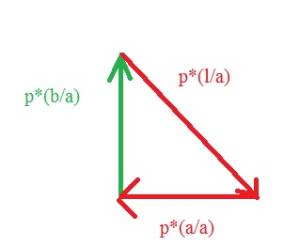
Risolvo la struttura considerando il solo carico P applicato nel punto B. Ottengo una distribuzione delle forze come in figura:
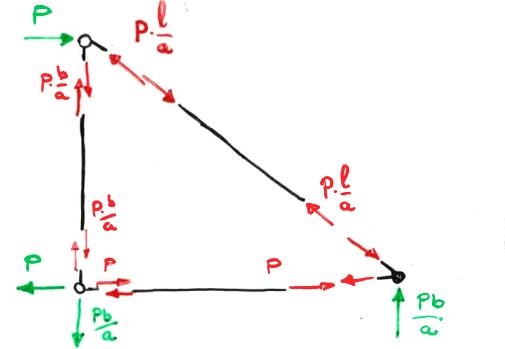
Notiamo che in questo caso sono presenti solamente azioni normali, considerate positivamente se di trazione e negativamente se di compressione. Le reazioni dei due vincoli a terra sono state trovate graficamente e impostando l'equilibrio alla traslazione a ciascun tratto di trave.
Il diagramma dello sforzo normale indotto dal carico P è:
Tutte le altre caratteristiche della sollecitazione sono nulle in ogni punto per quanto spiegato sopra.
Effetti della coppia $C_{B}$
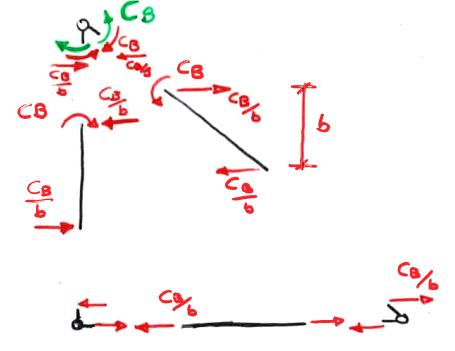
Considero ora i contributi relativi alla coppia CB ottenuta sostituendo al giunto rigido in B una cerniera. Dagli equilibri a rotazione e a traslazione ottengo il seguente bilanciamento di forze:
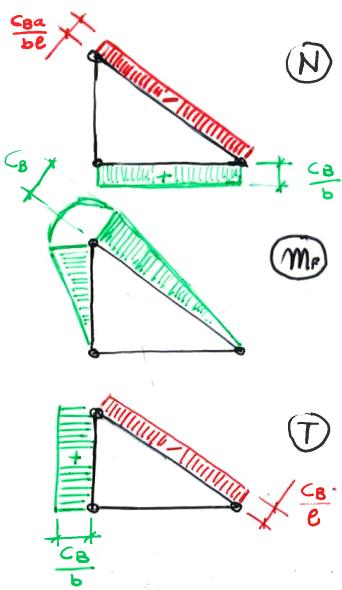
A cui corrispondono i seguenti diagrammi relativi ad azione normale, momento flettente e taglio, nell'ordine:
Effetti della coppia $C_{O}$
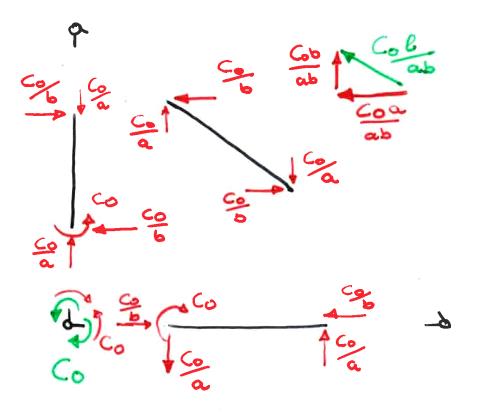
Considero ora i contributi relativi alla coppia CO ottenuta svincolando il giunto rigido in O. Dagli equilibri a rotazione e a traslazione ottengo il seguente bilanciamento di forze:
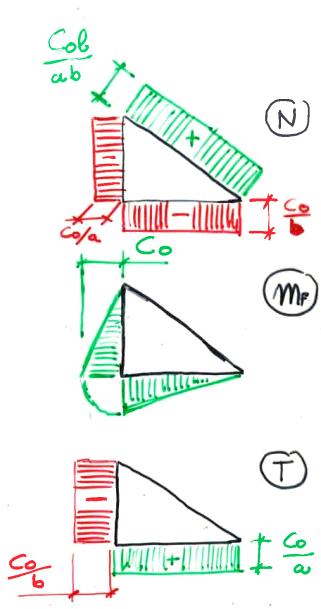
A cui corrispondono i seguenti diagrammi relativi ad azione normale, momento flettente e taglio, nell'ordine:
Effetti della coppia $C_{A}$
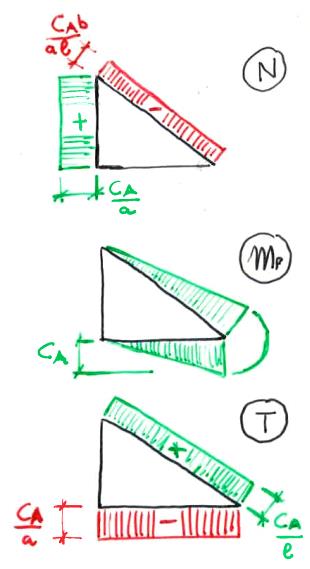
Considero ora i contributi relativi alla coppia CA ottenuta svincolando il giunto rigido in A. Dagli equilibri a rotazione e a traslazione ottengo il seguente bilanciamento di forze:
A cui corrispondono i seguenti diagrammi relativi ad azione normale, momento flettente e taglio, nell'ordine:
Maxima
Per effettuare i calcoli sulla maglia triangolare si redige il seguente codice in wxMaxima.
Come prima istruzione puliamo la memoria attraverso il comando:
kill (all) $
Le quantità a , b ed l , che rappresentano le lunghezze dei singoli lati, sono sempre positive; per rappresentare ciò in Maxima si utilizza il comando assume, che ci permette di fare delle ipotesi che saranno poi valide in tutto il resto del codice:
assume( a > 0 , b > 0 , l > 0 );
Il lato l è una grandezza derivata dalle lunghezze degli altri due lati, pertanto la riportiamo come:
ipo : [ l = sqrt (a^2 + b^2) ];
Avendo definito a , b ed l le assegniamo a delle variabili utili per la manipolazione al calcolatore:
l_OA : a ; l_OB : b ; l_AB : l ;
Dall'analisi della struttura è emerso che alcune caratteristiche di sollecitazione potrebbero avere un comportamento lineare lungo i lati della stessa, pertanto risulta comodo introdurre delle funzioni di forma, definite in modo tale che valgano 0 nel primo nodo di un lato ed 1 nel restante nodo. Attraverso l'interpolazione lineare di tali funzioni si definisce il comportamento lineare di una qualsiasi funzione agente nel tratto analizzato. Tali funzioni di forma vengono associate ai nodi del singolo lato della maglia, e come riferimento si utilizza una coordinata curvilinea adimensionalizzata ξ definita come rapporto tra una ascissa curvilinea s , che ha origine sul primo nodo di ogni singolo lato, e la misura del lato stesso; pertanto la coordinata ξ varierà all'interno del lato in questione tra 0 ( sul primo nodo ) e 1 ( sul secondo nodo ). Definiamo quindi le funzioni di forma N1 ed N2 come:
N1 : 1 - xi $ N2 : xi $
A questo punto siamo in grado di riportare le caratteristiche di sollecitazione , precedentemente calcolate tratto per tratto in funzione di P, CO , CA , CB , nel codice:
|- - - - -P - - - - - |- - - - - CB - - - - - |- - - - - CA - - - - - |- - - - - CO - - - - - | N_OB : 0 +P*b/a + 0 + CA/a - CO/a $ N_OA : 0 +P + CB/b + 0 -CO/b $ N_AB : 0 -P*l/a - CB*a/b/l - CA*b/a/l + CO*l/a/b $ Mf_OB : 0 +0 + 0*N1 + CB*N2 + 0 +CO*N1 +0*N2 $ Mf_OA : 0 +0 + 0 + 0*N1+CA*N2 +CO*N1 +0*N2 $ Mf_AB : 0 +0 + 0*N1 + CB*N2 + CA*N1 + 0*N2 + 0 $ T_OB : +0 + CB/b + 0 - CO/b $ T_OA : 0 +0 + 0 - CA/a + CO/a $ T_AB : 0 +0 - CB/l + CA/l +0 $
Prima di calcolare l'energia potenziale elastica definiamo la sezione e il materiale, e assegniamo ciò a delle variabili che richiameremo poi nei calcoli:
sezione : [ A=%pi*d^2/4, J=%pi*d^4/64, eta=111/100]; sezionecava: [ A=%pi*(d^2-(d*3/4)^2)/4,J=%pi*(d^4 – (d*3/4)^4)/64,eta=111/100]; isotropo : [ G = E/2/(1+nu) ];
Abbiamo cosi definito le condizioni per il calcolo di tale maglia in sezioni circolari e nell'ipotesi di materiale isotropo. Vengono inserite inoltre le ipotesi riguardanti una sezione cava con diametro interno pari a ¾ di quello esterno, per valutare graficamente la differente rigidezza tra maglie triangolari cave e piene (l'eta teoricamente varia, in questo caso lo lasciamo volutamente pari all'eta della sezione cava per fare un esempio di calcoli a confronto tra sezione cava e piena). Possiamo a questo punto calcolare l'energia potenziale elastica attraverso il comando integrate come:
U :
integrate(
( Mf_OB^2/2/E/J
+ N_OB^2/2/E/A
+ eta*T_OB^2/2/G/A
)*l_OB
,xi
,0
,1
)
+ integrate(
( Mf_OA^2/2/E/J
+ N_OA^2/2/E/A
+ eta*T_OA^2/2/G/A
)*l_OA
,xi
,0
,1
)
+ integrate(
( Mf_AB^2/2/E/J
+ N_AB^2/2/E/A
+ eta*T_AB^2/2/G/A
)*l_AB
,xi
,0
,1
)$
Si procede con il calcolo delle reazioni vincolari incognite, CO,CB e CA attraverso il teorema di Castigliano secondo cui la derivata dell'energia potenziale elastica U rispetto , ad esempio, CB è uguale all'angolo di apertura della cerniera in B, che deve essere uguale a 0 per coerenza con il vincolo interno originario secondo la continuità delle rotazioni al nodo. Tale procedimento va applicato in maniera analoga per ricavare CO e CA. Il sistema è lineare quindi ci si aspetta che le rotazioni di apertura delle cerniere siano lineari nelle sollecitazioni CA, CO , CB. P vale come parametro, le funzioni dipenderanno da P. Si imposta un sistema di 3 equazioni nelle incognite CO, CA, CB e si utilizza il comando linsolve per la risoluzione di sistemi di equazioni lineari:
caso_ipe : linsolve ( [ diff(U,CB)=0, diff(U,CO)=0, diff(U,CA)=0 ] ,[CB,CO,CA] ) $
Il linsolve darà l'espressione di CB,CO,CA; si attribuisce ciò a caso_ipe, che è l'espressione della struttura iperstatica con vincoli di incastro tra i membri. Si definisce un analogo caso isostatico con vincoli di cerniera interna sui membri, per fare un paragone con il caso iperstatico, mediante le ipotesi:
caso_iso : [ CB=0 , CO=0 , CA=0 ]$
In questo caso non abbiamo nessuna reazione a fronte dell'apertura delle cerniere stesse, non è vincolata l'apertura dei membri come il caso iperstatico. Sotto queste ipotesi si ricavano le energie potenziali elastiche per i due casi attraverso il comando di valutazione ev:
U_iso : ev(U, caso_iso);
U_ipe : ev(U, caso_ipe)$
A questo punto si ricavano i cedimenti delle strutture per i due casi sotto il carico P attraverso il comando diff che viene usato per calcolare la derivata dell'energia potenziale elastica rispetto al carico P nei due casi,:
delta_iso : diff(U_iso,P) $ delta_ipe : diff(U_ipe,P) $
Si valuta poi una lista contenente due contributi (delta_iso e delta_ipe) per calcolare la differente rigidezza tra caso iperstatico ed isostatico inserendo tutti i parametri numerici che servono :
ev( [ delta_iso , delta_ipe ], a=100, b=50, d=20, nu=0.3, E=1000, P=1000, ipo, sezione, isotropo, infeval );
Da cui poi ricaviamo un valore numerico:
% , numer ;
Si è utilizzato il comando infeval che reitera la valutazione sostituendo le variabili con le loro definizioni finché due valutazioni successive non risultano uguali tra loro.
In maniera analoga si poteva comparare la rigidezza della maglia iperstatica rispetto la sua modellazione a cerniere definendo il rapporto tra delta_iso e delta_ipe :
ratio : delta_iso/delta_ipe;
E valutando poi il caso generale così ricavato al variare di uno dei parametri, sotto delle ipotesi numeriche, ovvero considerando:
- b=a*1 in modo tale da avere condizioni di maglia triangolare isoscele (i cateti sono uguali).
- ipo sono le ipotesi di base su l.
- alpha è il rapporto tra il diametro della sezione e uno dei lati della maglia, è il parametro variabile. Risulta molto piccolo se il lato della maglia è snello, mentre se il suo valore è vicino ad 1 si parla di lato tozzo.
- isotropo riguarda il materiale,
- nu e* il coefficiente di Poisson.
- sezione ci da le caratteristiche della nostra sezione di maglia, definite precedentemente.
Ciò si traduce in:
myratio : ev(ratio, b=a*1, ipo, sezione, isotropo, nu=3/10, d=alpha*a, infeval );
Per rappresentare il tutto si crea un grafico con variabile indipendente alpha e variabile dipendente myratio. Per impostare le etichette a mano, si utilizza il comando legend che tramite una lista a cui si accodano delle stringhe (ovvero caratteri tra doppi apici) permette di riportare sul grafico le etichette scelte dall'utente .Per inserire il grafico nel nostro codice utilizziamo wxplot2d. Abbiamo così:
wxplot2d( myratio, [alpha,0,1] );
Dal grafico si vede che se il lato della maglia è sottile, quindi siamo in presenza di un diametro d contenuto, il caso isostatico e il caso iperstatico hanno la stessa rigidezza, ma mano a mano che il lato diventa tozzo invece la differenza tra i due casi diventa sempre maggiore. Se utilizzassimo maglie con lati non pieni, ma cavi questa differenza sarebbe molto più marcata. Per mostrare ciò si rivaluta myratio attraverso myratiocavo per mostrare le stesse procedure di prima, ma applicate ad una sezione cava in cui il diametro interno è pari a ¾ del diametro esterno:
myratiocavo : ev(ratio, b=a*1, ipo, sezionecava, isotropo, nu=3/10, d=alpha*a, infeval );
Infine viene riportato il grafico di entrambi i casi:
wxplot2d( [myratio,myratiocavo], [alpha,0,1], [legend,"Pieno","Cavo con di=(3/4)*de"] );
Autori, note e ringraziamenti
Autori
Alfonso Miccio mat. 100915, Antonio Cosentino mat. 97030,Lorenzo Bianco mat., Alessandro Guioli mat.






Discussione
REVISORE 1
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione?La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
No, non ho notato passaggi o formule che non rispecchiano le regole di composizione del testo.
Il testo proposto è coerente con gli appunti personali del revisore?
Si il testo proposto dai colleghi è coerente nelle immagini e nelle note, con gli appunti e la registrazione audio personale riguardante la lezione del revisore.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Le rappresentazioni e i disegni spiegati ed esposti dal docente durante la lezione, sono stati adeguatamente inseriti per facilitare la comprensione del testo proposto dai colleghi.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
A mio parere il testo è sufficientemente descrittivo per far comprendere i significati e gli aspetti trattati a lezione. Anche nella parte che riguarda la spiegazione degli aspetti trattati mediante il programma Maxima è sufficientemente dettagliata nelle parole e nelle formule, per far capire a chi legge, l’uso dei codici.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
Credo non sia necessario l’intervento del docente per chiarire passaggi o aspetti della trattazione.
Ore dedicate a questa revisione
Nella revisione sono state dedicate circa 4 ore, cioè il tempo per ascoltare la registrazione audio della lezione e quindi la successiva comprensione e verifica dei concetti esposti nella trattazione.
REVISORE 2:
ho appena finito di revisionare la lezione dei miei colleghi, e dopo un'attenta rilettura non ho riscontrato inesattezze o concetti mal formulati. Ho impiegato circa due ore per far ciò.