Indice
Thin walled profile in torsion
Please note that the techniques employed rely on the monoclinic nature of the material with respect to the cross-sectional plane, i.e. such a plane is required to be a symmetry plane for the material.
Open thin-walled rectangular cross section profile (a longitudinal cut is performed at the lateral wall center line, whose kerf (width) is negligible), 80x40mm at the midsurface, 6mm wall thickness. Element size of ~10mm. The severed lateral wall may be easily deactivated to reproduce the simplified ladder-frame chassis cross section.
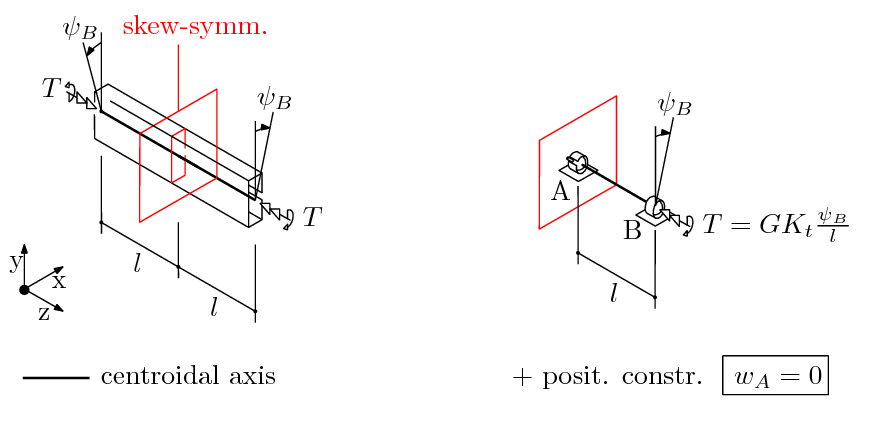
At the A cross section, a skew-symmetry material continuity constraint is applied.
The kinematic constraint at the B point (sphere in cylinder joint) is a positioning constraint, along with the $w_A=0$ axial constraint in A.
A twist per unit length equaling 0.001 radiant/mm is imposed to the profile, i.e. a $\psi_B=0.001 \cdot l$ rotation is imposed at each end, where $l$ is the $z$ axial coordinate of the endpoints, being z=0 at the skew-symmetry plane.
The reaction moment associated with the constraint will determine the applied torque $T$.
model at the end of the 2020-04-02 lesson
model at the end of the 2020-04-06 lesson
profile_in_torsion_a2020_v010.mfd
model at the end of the 2020-04-09 lesson
model at the end of the 2020-04-12 lesson, and the same model, with increasingly refined in-cross-section discretizations. Please observe (try it!) that no change in results is obtained by further splitting the elements in the axial directions; such a result is related to the fact that stresses are observed to be constant along the same direction.
LibreOffice/MSExcel spreadsheet for the collection and the normalization of the results, to be filled as homework.
At the end of the 2020-04-16 lesson: otw model, ctw model.
spreadsheet with increased profile length torsional_stiffness_evaluation_ffcd2020_v001.xls, and the associated otw model and ctw model.
Thin walled profile subject to pure shear
Various incremental steps in the definition of the shear loadcase v015 v016 v017 v018, and the updated spreadsheet. v018 is the final model for the response evaluation of the cross section to skew-symmetric internal action components ($M_t$,$Q_x$,$Q_y$).
Please note that, for the application of the presented procedure, the global (O,x) (O,y) axes must coincide with the principal axes of (elastic) inertia for the cross section.
Thin walled profile in bending
For reference/review purposes: last_year_notes_on_bending_and_shear.pdf. Please read attentively the first paragraph devoted to axial load and bending; if something is not clear, please ask the professor. Such a treatise should constitute just a slight extension of what you already encountered in previous Strength of Materials courses.
profile_in_bending_a2020_v001.mfd
profile_in_bending_a2020_v002.mfd
profile_in_bending_a2020_v003.mfd
Solution: FE model with unit curvature loadcases, Spreadsheet with the collected results, FE model re-oriented s.t. the global (O,x) (O,y) axes coincide with the principal axes of (elastic) inertia for the cross section, in order to proceed with the pure shear analysis.
Auxiliary maxima worksheet for literally solving the 2×2 eigenvalue problem.