Indice
QUADRILATERO ISOPARAMETRICO A 4 NODI
Quasi tutti gli elementi sono isoparametrici tranne il triangolare a 3 nodi. Ci concentriamo in particolare nell'elemento quadrilatero isoparametrico a 4 nodi nel caso di tensione piana.
Richiamo su stati di tensione piana
Per la tensione piana ricordo che tutte componenti non nulle delle tensioni sono nel piano, in particolare sono non nulle le $\sigma _{x}$,$\sigma _{y}$ e $\tau_{xy}$ invece sono nulle le componenti $\sigma _{z}$, $\tau_{xz}$ e $\tau_{yz}$. A causa della natura nulla delle $\tau$ si avrà che le deformazioni taglianti $\gamma_{xz}=0$, $\tau_{yz}=0$ ma in generale si avrà $\gamma_{xy} \neq 0$.
Analogamente si avranno le deformazioni assiali non nulle lungo x, lungo y e anche lungo z. Infatti, per effetto Poisson, vale la relazione:
$\epsilon _{z}=-\nu(\epsilon _{x}+\epsilon _{y})$ (questo quando $\sigma _{z}=0$)
per cui per lo stato di tensione piana si avrà la tensione nulla lungo z ma la deformazione non sarà, ma è definita dall'effetto Poisson come strizione associata ad allungamenti lungo x e y.
Questo stato di tensione è tipico di strutture sottili, quindi membrane o lamiere (caricate entro piano), o di qualsiasi corpo dotato di pareti sottili. Infatti si definisce anche stato membranale: quando lo spessore del corpo è molto minore rispetto alle altre dimensioni caratteristiche del corpo (per esempio la lastra piana forata). Quindi lavorando in tensione piana, avremo solo spostamenti u e v (rispettivamente lungo x e y) e invece w=0 (spostamento lungo z), dove x e y sono gli assi entro il piano in cui giace la struttura.
Ritorniamo sul quadrilatero .
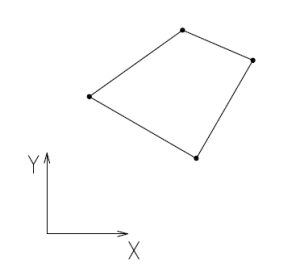
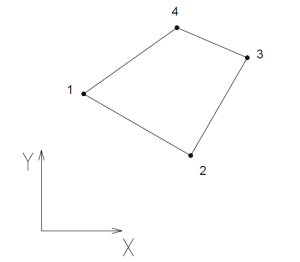
Dal punto di vista geometrico questo elemento ha la forma di un quadrilatero arbitrariamente deformato e avrò 4 gradi di libertà associati ai 4 nodi.
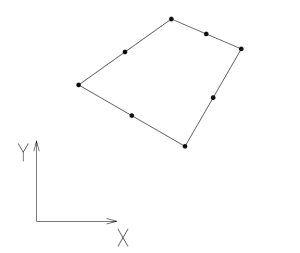
Esistono delle varianti con dei nodi aggiunti:
- quadrilatero a 8 nodi: gli altri 4 sono posti sul punto medio di ciascun lato.
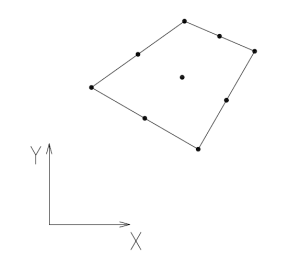
- quadrilatero a 9 nodi: rispetto al precedente avrò un nodo di centro elemento.
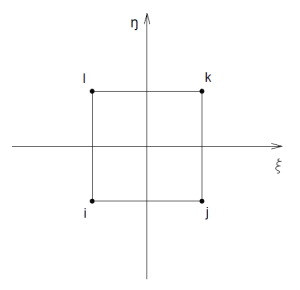
Per ora occupiamoci del 4 nodi. La natura di arbitrariamente deformata del quadrilatero complicherà un po' il caso, infatti basta pensare di dover integrare una grandezza nell'elemento e si nota che gli estremi di integrazione sono abbastanza complessi. Per cui si decide di utilizzare un piano ausiliario $O\xi\eta$, in cui qualsiasi quadrilatero diventa un quadrato centrato nell'origine del sistema di assi e i lati si estendono per $\xi=-1$ a $\xi=1$ e da $\eta=-1$ a $\eta=1$.
Si definiscono $(x,y)$ coordinate fisiche e invece $(\xi,\eta)$ coordinate naturali. Per cui passerò sempre da $(x,y)$ a $(\xi,\eta)$ proprio perché così l'elemento è regolare. Occorre definire quindi una corrispondenza dei punti tra il piano fisico e quello naturale, magari una relazione biunivoca: sarà facile passare da un punto nel sistema naturale $(\xi,\eta)$ al sistema fisico $(x,y)$, invece il contrario sarà matematicamente più complesso e varrà sotto varie ipotesi.
Questo lo si fa definendo una mappatura di una funzione che dal dominio naturale passa a quello fisico, ossia definendo $x(\xi,\eta)$ e $y(\xi,\eta)$. Per cui decido di dover definire delle funzioni a cui associano ad ogni punto $(\xi,\eta)$ un punto in $(x,y)$. Queste funzioni devono assicurare che i vertici diventeranno vertici e che i punti di centro lato diventeranno punti di centro lato nella loro immagine. L'idea è questa: mi costruisco 4 funzioni di forma per i 4 nodi dell'elemento in coordinate naturali, per cui avrò una funzione
$N_{1}(\xi,\eta)=1$ (sul nodo a cui è associata, per cui sul nodo 1 di coordinate (-1,-1)) e $0$ (su tutti gli altri 3 nodi, ossia su (-1,1),(1,-1), (1,1))
Scelgo di utilizzare l'interpolazione di tipo polinomiale e avendo quindi 4 condizioni (sui 4 nodi) potrò determinare 4 costanti. Sappiamo però che non esiste un polinomio lineare in funzione di 4 parametri (perché per averne una lineare ne servirebbero 3 come per l'elemento triangolare a 3 nodi). Pertanto scelgo la seguente forma bilineare:
$N(\xi,\eta)= a + b\cdot \xi +c\cdot \eta + d\cdot \xi\eta$
Osservazione: il termine $d\cdot\xi\eta$ è di natura quadratica, ma è quadratico all'interno dell'elemento, invece se mi muovo sulle rette a $\xi=cost$ oppure $\eta=cost$ questa funzione di forma è lineare, in particolare la funzione è lineare sui 4 lati del quadrilatero! (cosa che $d\xi^{2}$ o $d\eta^{2}$ non mi garantivano). Quindi si hanno 4 parametri da definire (a,b,c,d) e 4 condizioni sui nodi. Risolvendo il sistema di 4 equazioni si ottiene che le funzioni di forma sono tutte nella forma:
$N_{i}(\xi,\eta) =\frac{^{(1 \pm \xi)\cdot (1 \pm \eta)}}{4}$ con i=1,2,3,4
Dove i segni giusti si ricavano facilmente per ciascuna funzione verificando il valore della funzione sui nodi.
Si osserva che nel centroide tutte le funzioni di forma valgono 1/4 per cui la loro somma vale 1. A questo punto, definite le funzioni di forma (che possono essere usate come funzioni peso per dei valori ai nodi), io posso definire la mappatura $x(\xi,\eta)$ e $y(\xi,\eta)$ in questa maniera:
$x(\xi,\eta)= x_{1}\cdot N_{1}(\xi,\eta) + x_{2}\cdot N_{2}(\xi,\eta) + x_{3}\cdot N_{3}(\xi,\eta) + x_{4}\cdot N_{4}(\xi,\eta)$ $y(\xi,\eta)= y_{1}\cdot N_{1}(\xi,\eta) + y_{2}\cdot N_{2}(\xi,\eta) + y_{3}\cdot N_{3}(\xi,\eta) + y_{4}\cdot N_{4}(\xi,\eta)$
dove $x_{i}$ e $y_{i}$ sono le coordinate fisiche dei 4 nodi.
Questa è una forma di interpolazione di una generica funzione sul dominio quadrilatero. Queste funzioni hanno altre proprietà, ad esempio per ogni punto $(\xi,\eta)$ interno al dominio allora
$\sum_{i=1}^{4}N_{1}(\xi,\eta) =1$ (sono effettivamente funzioni peso) come notato in precedenza nel centroide.
Queste funzioni di forma posso usarle anche per definire le forme degli spostamenti:
$u(\xi,\eta)= u_{1}\cdot N_{1}(\xi,\eta) + u_{2}\cdot N_{2}(\xi,\eta) + u_{3}\cdot N_{3}(\xi,\eta) + u_{4}\cdot N_{4}(\xi,\eta)$ $v(\xi,\eta)= v_{1}\cdot N_{1}(\xi,\eta) + v_{2}\cdot N_{2}(\xi,\eta) + v_{3}\cdot N_{3}(\xi,\eta) + v_{4}\cdot N_{4}(\xi,\eta)$
$u(\xi,\eta)$ e $v(\xi,\eta)$ sono gli spostamenti di un qualsiasi punto interno al dominio del quadrilatero.
Avendo fatto questa scelta ben precisa, ossia usare le stesse funzioni di forma sia per la trasformazione di coordinate sia per la rappresentazione degli spostamenti (potevo fare anche una scelta diversa). Per cui si parla di elemento ISOPARAMETRICO. Invece si parla di elementi subparametrici o superparametrici a seconda che la mappatura sia più povera o più ricca degli spostamenti.
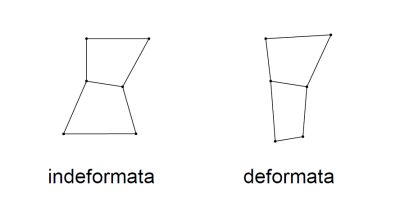
Configurazione indeformata/deformata
Lungo un segmento la funzione di mappatura è una funzione che è lineare sul perimetro mentre all’interno del dominio non lo è.
Se in un sistema di riferimento nodale un punto è intermedio tra due estremi di un segmento allora anche la sua immagine nel sistema di riferimento fisico dovrà essere intermedia tra i due nodi. Quindi se un lato nella sua configurazione indeformata è rettilineo dovrà esserlo anche nella sua configurazione deformata.
Se pure gli spostamenti sono funzioni lineari su ogni singolo lato, allora se il lato indeformato è rettilineo, un suo punto intermedio si muove come la media degli spostamenti dei due estremi del lato. E in generale, per un qualunque punto dell’elemento, lo spostamento deve essere la media pesata ( per es. con la regola della leva ) degli spostamenti dei punti agli estremi.
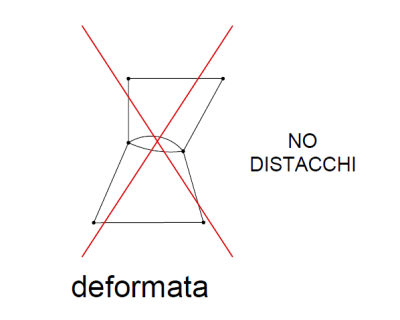
Ogni punto di un lato condiviso da due elementi quadrilateri a quattro nodi giace sul segmento che congiunge i due nodi in comune. Per questo lato deve valere che se un punto nasce intermedio sul lato condiviso nella configurazione indeformata deve rimanere intermedio sul lato anche nella configurazione deformata dell’elemento.
Non è possibile avere una discontinuità di spostamento tra i punti visti da entrambe le configurazioni.
Essendo gli spostamenti uguali ai due vertici ed essendo definiti per ambo gli elementi come interpolazione lineare degli spostamenti agli estremi è impossibile avere fenomeni di distacco, compenetrazione del materiale che causerebbero una perdita di rettilineità.
Questo non accade se all’elemento triangolare tre nodi tentassi di definire gli spostamenti nella forma come:
$u(x,y)= a+b\cdot x+c\cdot y+d\cdot xy$
La differenza tra questa formulazione e quella che abbiamo usato è che qui ho il termine quadratico espresso in coordinate fisiche (x,y) . In coordinate fisiche i lati non hanno la proprietà di avere x e y costanti per cui la funzione spostamento a+b\cdot x+c\cdot y+d\cdot xy non sarebbe lineare lungo i lati e potrebbe dar luogo a deformazioni che implicherebbero non continuità tra gli spostamenti o distacco del materiale.
La continuità degli spostamenti entro-elemento è garantita dalla continuità della funzione però il problema è che essendo funzioni definite continue a tratti non è scontato che ci sia continuità tra elemento ed elemento. La funzione di forma $u(x,y)= a+b\cdot x+c\cdot y+d\cdot xy$ si può utlizzare solo per elementi che sono rettangolari in (x,y) i cui lati sono paralleli a x e y.
Dagli spostamenti alle deformazioni
Ora abbiamo le forme di spostamento u e v e vogliamo ricavare le deformazioni riguardo $\varepsilon_{x}, \varepsilon_{y}, \gamma_{xy}$
Ma $\large \varepsilon_{x}= \frac{\partial u }{\partial x } = \frac{\partial u }{\partial \xi } \frac{\partial \xi }{\partial x } + \frac{\partial u }{\partial \eta } \frac{\partial \eta }{\partial x } $
ma poichè non conosco $\xi (x,y)$ e $\eta(x,y)$, dovrei definire una funzione inversa per ricavare $\xi (x,y)$ e $\eta(x,y))$ che non sono per nulla comode da definire.
Come agisco a passare quindi dagli spostamenti alle deformazioni? Posso scrivere:
$\large \frac{\partial u }{\partial \xi } = \frac{\partial u }{\partial x } \frac{\partial x }{\partial \xi } + \frac{\partial u }{\partial y } \frac{\partial y }{\partial \xi }$
$\large \frac{\partial u }{\partial \eta } = \frac{\partial u }{\partial x } \frac{\partial x }{\partial \eta } + \frac{\partial u }{\partial y } \frac{\partial y }{\partial \eta }$
Le quantità $\frac{\partial u }{\partial x }$ e $\frac{\partial u }{\partial x }$ risultano scomode da calcolare e risulteranno le quantità incognite.
Ricordando che : $\frac{\partial u }{\partial \eta } = U_{1}\cdot \frac{\partial N_{1} }{\partial \eta }(\xi,\eta) + U_{2}\cdot \frac{\partial N_{2} }{\partial \eta }(\xi,\eta) + ...$
Posso ora quindi vedere le equazioni sopra scritte come un sistema lineare: in cui le incognite sono gli oggetti scomodi da calcolare :
$\large \begin{bmatrix} \frac{\partial u }{\partial \xi}\\ \frac{\partial u }{\partial \eta } \end{bmatrix} = \begin{bmatrix} \frac{\partial x }{\partial \xi } & \frac{\partial y }{\partial \xi }\\ \frac{\partial x }{\partial \eta } & \frac{\partial y }{\partial \eta } \end{bmatrix} \begin{bmatrix} \frac{\partial u }{\partial x }\\ \frac{\partial u }{\partial y } \end{bmatrix}$
Il vettore colonna $\begin{bmatrix} \frac{\partial u }{\partial x }\\ \frac{\partial u }{\partial y } \end{bmatrix}$ è il formato dalle quantità incognite
Jacobiana
La matrice $\begin{bmatrix} \frac{\partial x }{\partial \xi } & \frac{\partial y }{\partial \xi }\\ \frac{\partial x }{\partial \eta } & \frac{\partial y }{\partial \eta } \end{bmatrix}$ è la matrice Jacobiana $J(\xi,\eta)$ ed risulta essere la matrice particolare funzione della trasformazione di coordinate (passaggio dai sistemi di riferimento $(\xi,\eta)$ a (x,y) ).
Questa matrice viene chiamata matrice JACOBIANA ed è funzione di $(\xi,\eta)$.
ATTENZIONE! In generale questa matrice non è la vera matrice Jacobiana classica ma è la trasposta di quella che sarebbe la definizione classica di JACOBIANA.
Noi chiameremo Jacobiana questa ( in matlab non è questa ).
Se J è invertibile, allora esiste una matrice inversa $J^{-1}$ tale che
$\large J^{-1}\begin{bmatrix} \frac{\partial u }{\partial \xi}\\ \frac{\partial u }{\partial \eta } \end{bmatrix} = \begin{bmatrix} \frac{\partial u }{\partial x }\\ \frac{\partial u }{\partial y } \end{bmatrix}$ e sarei così in grado di ricavarmi le incognite.
Matrice Inversa
Come si ottiene una matrice inversa?
Se per esempio avessimo una matrice siffatta: $\large A = \begin{bmatrix} a & b\\ c & d \end{bmatrix}$; $\large A^{-1} =\frac{1}{det(A)}=\frac{1}{ad-bc} \cdot \begin{bmatrix} d & -b\\ -c & a \end{bmatrix}$
A deve essere non singolare! Allora la condizione da soddisfare è che ad-bc > 0. Chiedere che la matrice sia invertibile equivale a dire che il prodotto di ad-bc > 0 . In realtà questi termini sono puramente funzione delle coordinate nodali e delle funzioni di forma.
Ma quando un elemento ha una J non invertibile (quindi singolare)?
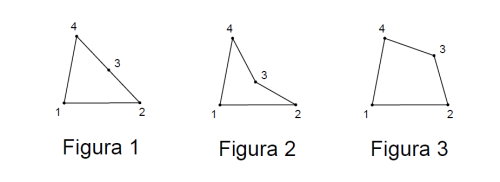
Analizziamo un elemento quadrilatero critico (quadrilatero con due lati allineati come in figura 1)
Elementi come in figura 1 hanno J=0.
Elementi come in figura 2 hanno in qualche punto dentro l’elemento stesso un J =0 e in più di un punto uno J<0.
Elementi in cui il nodo 3 nodo è leggermente spostato verso l’esterno rispetto alla retta che congiunge 2 con 4 ( figura 3 ) hanno uno J che è sempre > 0.
Molte volte basta analizzare la geometria dell’elemento nella sua forma indeformata per valutare la singolarità e quindi l'invertibilità della matrice J.
Deformazioni
Salvo geometrie del genere quella matrice è invertibile e posso ricavare ad esempio $\frac{\partial u }{\partial x }$ in funzione degli spostamenti nodali. Ed è ora possibile ricavare le deformazioni.
Proviamo a generalizzare questa formulazione in
$ \varepsilon _{x},\varepsilon _{y} , \gamma _{xy} $ sono definite come premoltiplicazione di una matrice che chiamo H per il vettore che contiene le quattro derivate dei due spostamenti nei due assi coordinati x e y.
Abbiamo poi introdotto una matrice 4 x 4 definita a blocchi che premoltiplica il vettore colonna
$\begin{bmatrix}
\frac{\partial u}{\partial \xi}
\frac{\partial u}{\partial \eta}
\frac{\partial v}{\partial \xi}
\frac{\partial v}{\partial \eta}
\end{bmatrix}^{T}$
Questa matrice presenta 4 blocchi 2×2 di cui gli extradiagonali sono nulli perché non c’è nessuna correlazione ad esempio tra $ \frac{\partial u}{\partial x}$ e $\frac{\partial v}{\partial \xi}$
A questo punto devo definire $ \frac{\partial u}{\partial \xi}$ e $ \frac{\partial u}{\partial \eta} $ in funzione degli spostamenti nodali da una parte e delle derivate delle funzioni di forma dall’altra parte.
Gli spostamenti all’interno dell’elemento sono combinazioni lineari degli spostamenti nodali con le funzioni di forma come peso per cui (e cosi saranno anche le derivate degli spostamenti in $(\xi,\eta)$ ) saranno funzioni lineari degli spostamenti nodali. Ogni dipendenza lineare può essere rappresentata con la premoltiplicazione di una matrice con le variabili indipendenti.
Questa matrice la posso costruire, infatti i termini sono tutti facilmente calcolabili perché le funzioni di forma sono facilmente derivabili in \xi e \eta e questo oggetto la chiamo matrice Q che è in funzione di $(\xi,\eta)$. Posso quindi scrivere $ \varepsilon =H\cdot J_{INV}^{*}(\xi,\eta)\cdot Q(\xi,\eta)\cdot \delta=B(\xi,\eta)\cdot \delta $
La matrice $J_{INV}^{*}(\xi,\eta)$ non è facilmente gestibile in quanto contiene un polinomio di ordine al massimo due al denominatore quindi una funzione razionale fratta in funzione di $(\xi,\eta)$. Anche la matrice Q è funzione $(\xi,\eta)$ e quindi abbiamo esplicitato la dipendenza dagli spostamenti $\delta$ La matrice B però a differenza dell’elemento triangolare a tre nodi non è costante ma è dipendente da $(\xi,\eta)$.
Tensioni
A questo punto ho definito le mie deformazioni in funzione degli spostamenti nodali ho deciso che il legame costitutivo del materiale è in tensione piana quindi esiste una matrice D tale per cui $ \sigma =D\cdot \varepsilon $
Per un materiale omogeneo isotropo in tensione piana posso scrivere:
Matrice di rigidezza
Ricavate le tensioni, a questo punto mi ricordo la procedura che ho utilizzato per estrarre la matrice rigidezza dell’elemento triangolare tre nodi che passa per una forma energetica. In particolare considero il quadrilatero 4 nodi sul mio piano $(x,y)$ portato in una configurazione deformata descritta ad ogni nodo sommato in forma vettoriale il suo spostamento.
La configurazione deformata, salvo che lo spostamento non sia moto di corpo rigido, esso comporta una reazione elastica del materiale che deve esser vinta da delle forze esterne F necessarie a mantenere la configurazione deformata. L’energia potenziale elastica interna dell’elemento deve essere uguale al lavoro compiuto dalle forze esterne per mantenere la configurazione deformata. Il lavoro è definito come $ W=\frac{1}{2}\cdot \bar{\delta^{T}}\cdot \bar{F}=\frac{1}{2}\cdot \sum_{i=1}^{8}\delta_{i}\cdot F_{i} $
$ \frac{1}{2} $ deriva dal fatto che le forze F sono quelle che agiscono a fine deformazione. Queste forze non sono rimaste costanti per tutta l’evoluzione del sistema ma sono passate da un valore nullo (configurazione indeformata) a un valore pari ad F nell’intorno in cui lo stato è deformato.
Energia potenziale elastica all’interno dell’elemento
$U=\frac{1}{2}\int_{V} \bar{\varepsilon} ^{T} \cdot \bar{\sigma} \cdot dV
=\frac{1}{2} \cdot t \int_{a}\begin{bmatrix}
\varepsilon_{x} \
\varepsilon_{y}\
\gamma_{xy}
\end{bmatrix}
\cdot \begin{bmatrix}
\sigma _{x}
\sigma _{y}
\tau _{xy}
\end{bmatrix}^{T} \cdot da
=\frac{1}{2} \cdot \bar{\delta}^{T} \cdot [t \int_{a} \bar{\bar{B}}(\xi, \eta) \cdot \bar{\bar{D}} \cdot \bar{\bar{B}}(\xi, \eta) \cdot da] \cdot \bar{\delta}$
Nel caso piano si riduce all’integrale sull’area (forze costanti sul volume), posso allora portar fuori lo spessore perché costante. Nel triangolare a tre nodi non abbiamo usato spessore perché abbiamo ricondotto tutto a spessore unitario: ossia le forze esterne sono forze per unità di spessore di struttura.
Quindi bisogna risolvere l’integrale,trovando un modo per svolgerlo senza determinare la primitiva. Occorre definire il da in funzione di $(\xi, \eta) $ così da avere gli estremi d’integrazione che vanno da -1 a 1 considerando però una costante di scala.
L’area del triangolino infinitesimo viene calcolata con la regola del determinante
Prima di calcolare il determinante della matrice posso semplificarla utilizzando alcune regole: Il determinante di una matrice non cambia se sommo a una riga una composizione lineare delle altre. Prendo allora la seconda riga e sottraggo la prima riga moltiplicata per x, faccio lo stesso con la terza riga a cui sottraggo la prima riga moltiplicata per y. Inoltre se uno scalare moltiplica un’intera riga o un’intera colonna della matrice può essere tirato fuori dal determinante. Mi ricordo poi che posso svolgere questo determinante con la regola dei minori
$ A_{tri,\xi\eta}=\frac{1}{2}d\xi d\eta $ è l'area del triangolino in $(\xi,\eta)$
Il rapporto delle aree dei due triangolini è dato dal determinante della matrice Jacobiana definita nel punto in cui ha origine il triangolo, in questo caso $(\xi,\eta)$.
Quindi la matrice di rigidezza per il quadrilatero isoparametrico a 4 nodi sarà:
$ K=t\cdot \int_{-1}^{1}\int_{-1}^{1} B^{T}(\xi,\eta)\cdot D \cdot B \begin{vmatrix}J(\xi,\eta) \end{vmatrix}d\xi d\eta $
Tabella di monitoraggio carico orario
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | |
|---|---|---|---|---|---|
| Giovanni Colangelo | 3 | — | — | — | — |
| Riccardo Bergamaschi | 3 | — | — | — | — |
| Ottaviani Giacomo | 3 | — | — | — | — |
| Arzilli Francesca | 3 | — | — | — | — |
| Rossella Testa | — | 1 | — | — | — |
| Antonio Cosentino | 2 | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | — | — | — | — | — |

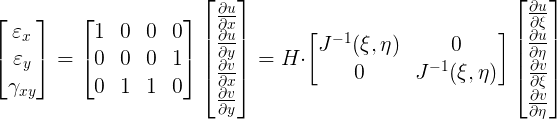
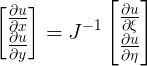
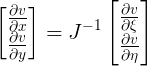
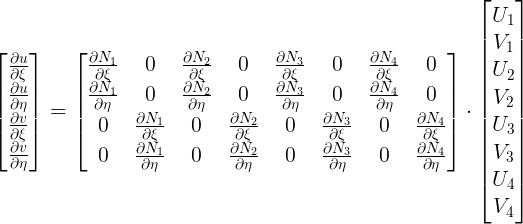
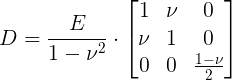
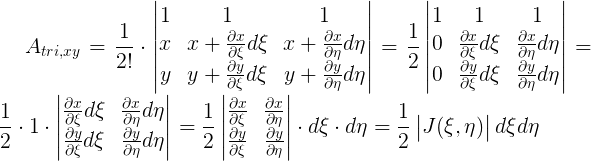
Discussione
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
Non richiedo alcuna correzione. Formule, passaggi ed immagini sono tutti corretti.
Il testo proposto è coerente con gli appunti personali del revisore?
Si.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Il numero di immagini è sufficiente.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Gli appunti sono sufficienti alla preparazione e non ritengo opportuna alcuna modifica.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
No.
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
Il lavoro svolto dai miei colleghi è abbastanza curato e completo, ho riscontrato soltanto alcune sviste dovute credo più ad errori di battitura che a mancata comprensione:
- La formula di Poisson vista a lezione si basa sulle deformazioni e non sulle tensioni. - Nella parte finale del paragrafo sulla deformata la formula degli spostamenti in coordinate fisiche si riferisce al quadrilatero 4 nodi. - Nella matrice 2×2 del paragrafo “Dagli spostamenti alle deformazioni” bisogna sostituire la derivata di x in eta al primo rigo con la derivata di x in csi. - Nella formula dell'energia potenziale elastica 1/2 andrebbe messo a moltiplicare.
Il testo proposto è coerente con gli appunti personali del revisore?
Si, risulta abbastanza completo.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Probabilmente l'aggiunta di una figura che mostri l'area del triangolino infinitesimo renderebbe più curata una trattazione che per il resto risulta completa.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Penso che sia sufficiente seguire questi appunti per una buona preparazione.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
Non credo sia necessario.
Varie ed eventuali.
..completare…
Spazio per eventuali note destinate al solo curatore (da non comunicarsi agli autori).
..completare…
Ore dedicate a questa revisione
2 ore.