Indice
Analisi di risposta per sovrapposizione modale
Abbiamo visto che l'analisi di risposta in frequenza di un telaio è abbastanza onerosa, mentre l'estrazione dei modi propri è un'analisi abbastanza rapida a livello di elementi finiti; sarebbe dunque utile se fosse possibile realizzare sulla base dei modi propri la riposta in frequenza, ed è quello che vedremo ora.
Supponiamo di aver estratto modi e frequenze proprie, perciò per l' i-esimo modo di vibrare abbiamo la pulsazione naturale
$$
\omega_i=2 \pi f_i
$$
ed i modi propri $\hat{x_i}$ normalizzati a massa unitaria.
Per esempio nel caso della lamella il primo modo era quello flessionale, ed ogni nodo si spostava in direzione normale alla lamella senza spostamenti entro piano; il vettore $\hat{x_i}$ è composto dagli spostamenti nodali $u, v, w, \theta_x, \theta_y, \theta_z$ di ogni nodo che costituisce la lamella, con unici valori non nulli $w$ e $\theta_y$.
Prendiamo due autovettori distinti $\hat{x_i}$ ed $\hat{x_j}$, e per essi esistono delle relazioni di ortogonalità:
$$
{\hat{x_j}}^T M \hat{x_i} = \delta_{ji} \\
{\hat{x_j}}^T K \hat{x_i} = \delta_{ji} {\omega_i}^2
$$
dove $\delta_{ji}$ vale $1$ se $i=j$ e $0$ se $i\ne j$.
L'analisi modale mi dà un numero finito di modi e frequenze proprie, e per esempio possiamo andare ad estrarre i primi $10$ modi propri: in questo modo si ottiene un sottoinsieme di modi propri che va da $1$ a $m$ con $m<n$ (se vado ad estrarre i primi $10$ modi propri ho che $m=10$). Possiamo prendere questi autovettori e costruire una matrice in modo che le colonne corrispondano agli $m$ vettori associati ai modi propri:
$$
\begin{bmatrix} \mid & \mid & \cdots & \mid \\
\hat{x_1} & \hat{x_2} & \cdots & \hat{x_m}\\
\mid & \mid & \cdots & \mid
\end{bmatrix}
$$
Essa ovviamente non è una matrice quadrata in quanto presenta $m$ colonne ed $n$ righe; se prendessi tutti gli $n$ gradi di libertà, ottengo $n$ vettori e combinandoli riesco ad ottenere qualsiasi stato deformativo della struttura: essendo $m<n$, combinando i vettori ottengo un sottoinsieme delle possibili deformazioni del sistema, perciò posso escludere le possibilità di deformazione che non ritengo idonee per la mia struttura nell'analisi.
A questo punto scrivo uno spostamento ipotetico definito come combinazione lineare secondo i singoli modi propri, dove i vari $\xi$ sono coefficienti che scalano linearmente il singolo modo proprio nella combinazione:
$$
\bar{x}=\hat{x_1} \xi_1 + \hat{x_2} \xi_2 + \cdots + \hat{x_m} \xi_m = \hat{X} \bar{\xi}
$$
Il vettore $\bar{x}$ così trovato lo vado a sostituire nell'equazione della risposta in frequenza: $$ (-\omega^2 M + j\omega C + K)\bar{x} = \bar{f} $$ che quindi diventa: $$ (-\omega^2 M + j\omega C + K)\hat{X} \bar{\xi} = \bar{f} $$ Dunque ho un sistema di $n$ equazioni in $m$ incognite, perciò non riuscirò in generale ad annulare il residuo che sarà pari a : $$ (-\omega^2 M + j\omega C + K)\hat{X} \bar{\xi}- \bar{f}=0 $$ Ciò che è possibile fare è annullare la proiezione sulle combinazioni lineari delle colonne della matrice $\hat{X}$: se per esempio $n=3$ ed $m=2$, con gli autovalori definisco un piano nello spazio tridimensionale, ed il residuo è un punto in questo spazio; non riuscirò mai a portarlo nell'origine, ma combinando gli autovalori posso proiettare il residuo sul piano, e portare nell'origine la proiezione del residuo entro piano. Per proiettare un vettore in un sottospazio devo eseguire il prodotto scalare: $$ {\hat{x}_1}^T \cdot [(-\omega^2 M + j\omega C + K)\hat{X} \bar{\xi}- \bar{f}]=0\\ \vdots \\ {{\hat{x}}_j}^T \cdot [(-\omega^2 M + j\omega C + K)\hat{X} \bar{\xi}- \bar{f}]=0\\ \vdots \\ {{\hat{x}}_m}^T \cdot [(-\omega^2 M + j\omega C + K)\hat{X} \bar{\xi}- \bar{f}]=0 $$ In questo modo ottengo $m$ equazioni in $m$ incognite, ed il sistema torna ad essere risolubile; in forma compatta posso scrivere: $$ {\hat{X}}^T \cdot [(-\omega^2 M + j\omega C + K)\hat{X} \bar{\xi}- \bar{f}]=0 $$
La matrice di smorzamento non ha nessuna proprietà particolare relativamente agli autovettori, e questo è un grande problema perchè non si può andare avanti nella trattazione; per questo motivo diciamo che la matrice di smorzamento non è generica, ma ipotizzo che essa sia combinazione lineare della matrice massa e della matrice rigidezza:
$$
C = \alpha M + \beta K
$$
In generale invece sappiamo solo che per un sistema ad $n$ gdl essa deve essere simmetrica e quindi è definita da ${n^2}/2$ elementi, mentre in questo caso essa è definita solo da due parametri $\alpha$ e $\beta$.
In questo modo nella formula rimangono solamente le matrici massa e rigidezza, e risulta che:
$$
{\hat{X}}^T M \hat{X} = I \\
{\hat{X}}^T K \hat{X} = \Lambda
$$
dove $\Lambda = diag({\omega_i}^2)$ è una matrice diagonale contenente la successione delle $m$ pulsazioni proprie.
Quindi il sistema di equazioni diventa:
$$
(-\omega^2 I+ j\omega (\alpha I + \beta \Lambda) + \Lambda)\bar{\xi} =\bar{q}
$$
dove $ \bar{q} = {\hat{X}}^T \bar{f}$., e le sue componenti sono $q_i={\bar{x}_i}^T f_i$ con $i=1,...,m$.
A questo punto mi accorgo che tutte le matrici che moltiplicano le incognite sono diagonali, perciò la matrice di sistema sarà diagonale e quindi le equazioni sono disaccoppiate, ovvero le $m$ equazioni sono indipendenti ed hanno la seguente forma:
$$
(-\omega^2 + j\alpha \omega + j\beta \omega {\omega_i}^2 + {\omega_i}^2)\bar{\xi} =\bar{q_i} \\ i=1,...,m
$$
e da questa equazione trovo \bar{\xi}.
Questa è equivalente all'equazione algebrica associata ad un oscillatore ad un grado di liberta con incognita di spostamento $\bar{\xi}$, $m=1$, $k={\omega_i}^2$ e $ c=2 \omega_i \zeta_i $.
Quindi ottengo un'equazione di un oscillatore equivalente per ogni modo proprio, e la $\xi_i$ mi dice quanto il modo proprio deve essere modulato per ottenere la soluzione; quindi il sistema iniziale corrisponde ad un sistema ad $m$ gradi di libertà, poi lo disaccoppio ottenendo $m$ oscillatori ad $1$ gdl ed ottengo l'equazione scritta sopra.
Le formule per trovare $\xi_i$ sono :

Dunque estraggo i modi propri, poi mi assicuro che essi siano stati normalizzati dal software a massa modale unitaria, poi calcolo i prodotti scalari tra i modi propri e la forzante, dopodichè noti per ogni modo proprio i $q_i$ posso trovare $\xi_i$ tramite le formule viste sopra, per sapere di quanto il modo proprio deve essere modulato.
L'inertanza dinamica del telaietto visto nelle scorse lezioni poteva essere calcolata estraendo i modi propri, estraendo poi il prodotto tra la forza esterna unitaria e lo spostamento del centro ruota per trovare $q_i$, con i quali poi posso ricavare $\xi_i$ e quindi trovare la risposta.
Per quanto riguarda l'ipotesi fatta sulla matrice di smorzamento, bisogna fare qualche precisazione sulla validità del risultato;
la matrice delle masse e la matrice delle rigidezze sono matrici sparse, mentre se ho una struttura che ha solo uno smorzatore
tra due gradi di libertà la matrice di smorzamento è ben diversa.
Considero uno smorzatore con coefficiente di smorzamento $c$ che collega il nodo $135$ con il nodo $182$; gli spostamenti
di questi nodi sono corrispondenti a dati valori del vettore delle incognite, per esempio:
$$
U_{182} = \delta_{803}
U_{135} = \delta_{512}
$$
La matrice di smorzamento è tutta nulla tranne in quattro elementi, che si trovano incrociando la righe 512 e 803 con le colonne 512 e 803:
$$
\begin{vmatrix} c & -c \\
-c & c
\end{vmatrix}
$$
Risulta impossibile ottenere tale matrice come combinazione lineare tra le matrici sparse di masse e rigidezze.
Dunque quando la struttura ha elementi smorzanti concentrati, questa procedura è assolutamente poco indicata e
bisognerà utilizzare la risposta in frequenza normale.
Nel caso invece in cui lo smorzamento sia strutturale, esso è definito proporzionale alla matrice di rigidezza e quindi
è possibile definire la matrice di smorzamento in forma di Rayleigh.
A cosa serve inserire lo smorzamento?
Serve ad esempio a fornire dei valori limitati di risposta in corrispondenza dei picchi di risonanza.
Sappiamo che “r” è definito come rapporto tra la pulsazione della forzante e la pulsazione propria dell'i-esimo modo proprio :
$$ r = \frac{\omega}{\omega_i} $$
Quando sono sulla risonanza dell'i-esimo modo proprio si ha $ r=1 $. Di conseguenza $ a_i = 0 $ e $ b_i $ è non nullo solo se c'è uno smorzamento.
Se ci mettiamo nel caso di risonanza e assenza di smorzamento sia $ a_i $ che $ b_i $ sono nulli e pertanto si perviene alla condizione per cui $ \left | \overline{\xi} \right | = \infty $ , a fronte di un numeratore finito (salvo il caso particolare in cui $ q_i = 0 $, ossia forzante e modo proprio siano perfettamente ortogonali).
Quindi l'unico modo per avere risposte finite in corrispondenza di una risonanza eccitata è avere uno smorzamento.
Quanto vale lo smorzamento?
Lo smorzamento strutturale, ovvero quello proprio dei materiali, i quali non essendo perfettamente elastici dissipano un po' di energia al loro interno, è molto basso, anche in riferimento allo smorzamento che si misura sulla struttura. Pertanto introducendo solo lo smorzamento strutturale si commetterebbe un errore andando a sovrastimare le risposte in risonanza.
Altre fonti di dissipazione di energia e quindi di smorzamento, sono date ad esempio dallo schiacciamento fisico dei film d'olio ai cuscinetti di supporto di un albero motore: l'effetto pompante durante la vibrazione (l'albero vibra a flessione e a torsione) dissipa energia.
Nel caso di un telaio gli elementi smorzanti sono: tutti i giunti incollati (la colla è un materiale polimerico, per cui smorza di più dell'acciaio), tutti i giunti rivettati (fenomeni di microslittamento per attrito, non lineari, che dissipano energia) e tutti i giunti bullonati. Inoltre, per attenuare il rumore, gran parte dei pannelli del telaio sono ricoperti di materiale dissipante (di solito schiume).
Quindi cosa usare come damping ratio di riferimento?
Possiamo far riferimento ai seguenti articoli, che si riferiscono perlopiù a casi civili:
https://engineering.purdue.edu/~ce573/Documents/Structural%20damping%20values_JDStevenson.pdf
http://iopscience.iop.org/1742-6596/268/1/012022/pdf/1742-6596_268_1_012022.pdf
http://teaching.ust.hk/~mech300/mech300_7_1_damping_ref.pdf
http://www.vibrationdata.com/tutorials/bolted_joint_damping.pdf
Approfondimenti sul problema dell'instabilità : Linearized Pre-Buckling Analysis
Abbiamo visto la procedura che prevede due livelli di carico : un livello $ 0 $ e un livello $ 1 $, o meglio due stati di equilibrio $0$ e $1$. 
In questi stati di equilibrio si considerano le matrici di rigidezza tangenti $\underline{\underline{K}}$, ossia quelle matrici che legano la variazione dello spostamento $\Delta\delta$ alla variazione della forza $\Delta{F}$ nell'intorno della condizione di equilibrio:
$$ \underline{\underline{K_1}} \underline{\Delta\delta} = \underline{\Delta{F}} $$
dove il pedice $1$ si riferisce all'intorno della configurazione 1.
Dato quindi uno spostamento $\underline\delta_1$ proprio della configurazione di equilibrio, che è in equilibrio con un carico $\underline{F_1}$, cosa succede quando vario il carico da $\underline{F_1}$ a $\underline{F_1} + \underline{\Delta{F_1}}$ ?
$\underline\delta_1$ non sarà più in equilibrio col carico variato, ma dovrà assestarsi in modo da ottenere una configurazione variata in spostamento a fronte di una perturbazione del carico.
La matrice di rigidezza tangente lega la variazione di spostamento alla variazione di carico, e quando essa è singolare è possibile avere una variazione di spostamento non nulla a fronte di una variazione di carico nulla:
$$ \underline{\underline{K}} \underline{\Delta\delta} = 0 $$
con $$ \underline{\Delta\delta} \ne 0 \Leftrightarrow det\underline{\underline{K}} = 0 $$
Nei software la condizione di equilibrio $0$ è quella scarica ($0$ coincide con l'origine degli assi del diagramma $F-\delta$) e come condizione di equilibrio $1$ si prende quella sotto carico di riferimento.
Per passare da stato $0$ a stato $1$ Marc fa un'evoluzione lineare elastica da stato $0$ a stato $1$ per poi ricalcolare la matrice di rigidezza, la quale può essere diversa tra stato $0$ e stato $1$. 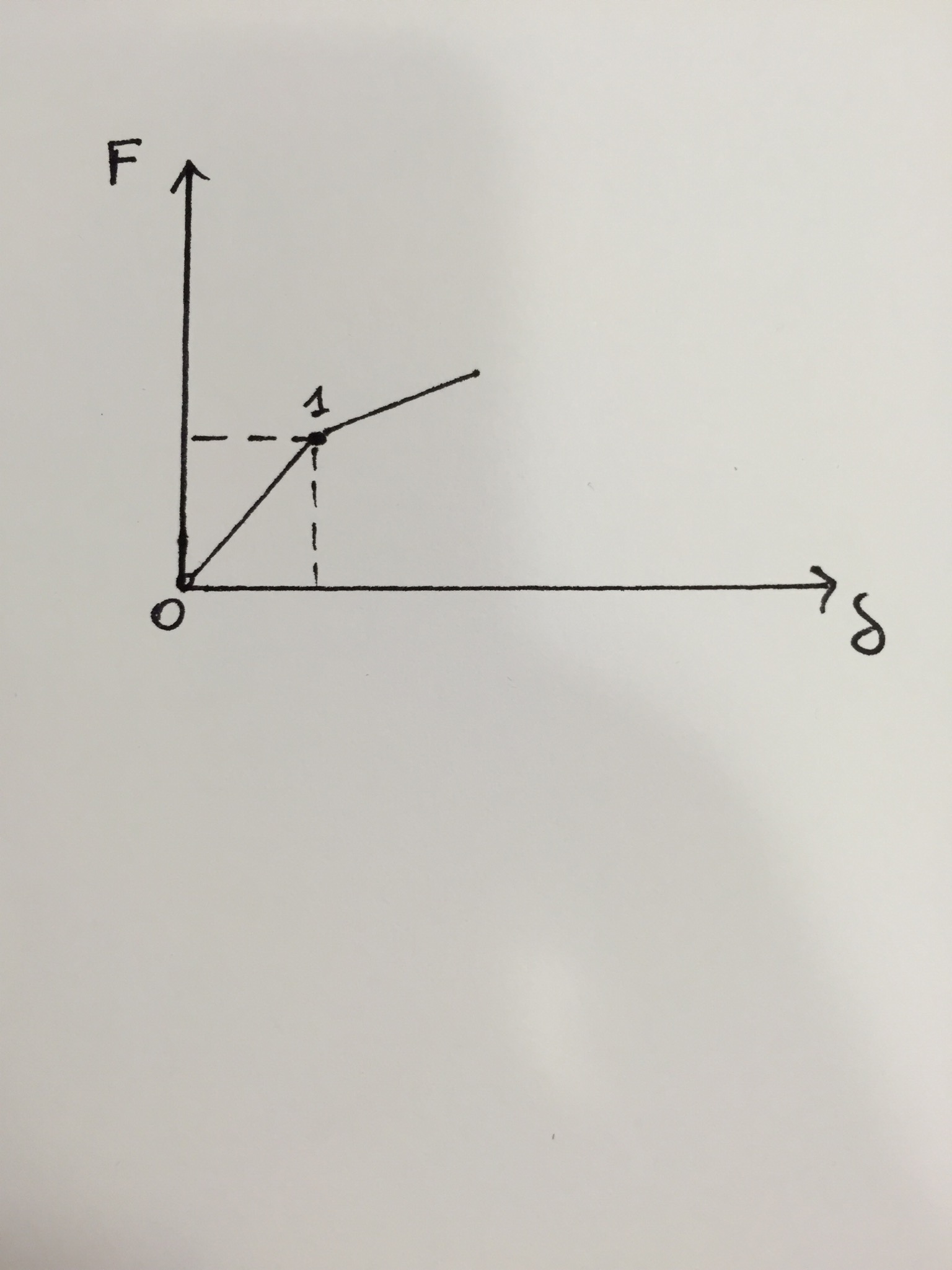
Si avrà quindi una matrice $\underline{\underline{K_0}}$ nell'intorno dello scarico e una matrice $\underline{\underline{K_1}}$ nell'intorno del caricato. In realtà il passaggio non è esattamente lineare elastico : vediamo come si svolge.
$\underline{\underline{K_0}}$ la prendo da struttura indeformata scarica (come prima) , mentre $\underline{\underline{K_1}}$ è definito diversamente:
$$ \underline{\underline{K_1}} = \underline{\underline{K_0}} + \underline{\underline{K_G}} $$
dove $\underline{\underline{K_G}}$ è detta “matrice geometrica” ed è stimata come $\underline{\underline{K_1}} - \underline{\underline{K_0}}$ scalata del fattore $\lambda$.
Come stimare $\underline{\underline{K_G}}$?
Si suppone di avere una struttura discretizzata in configurazione indeformata pre-caricata :
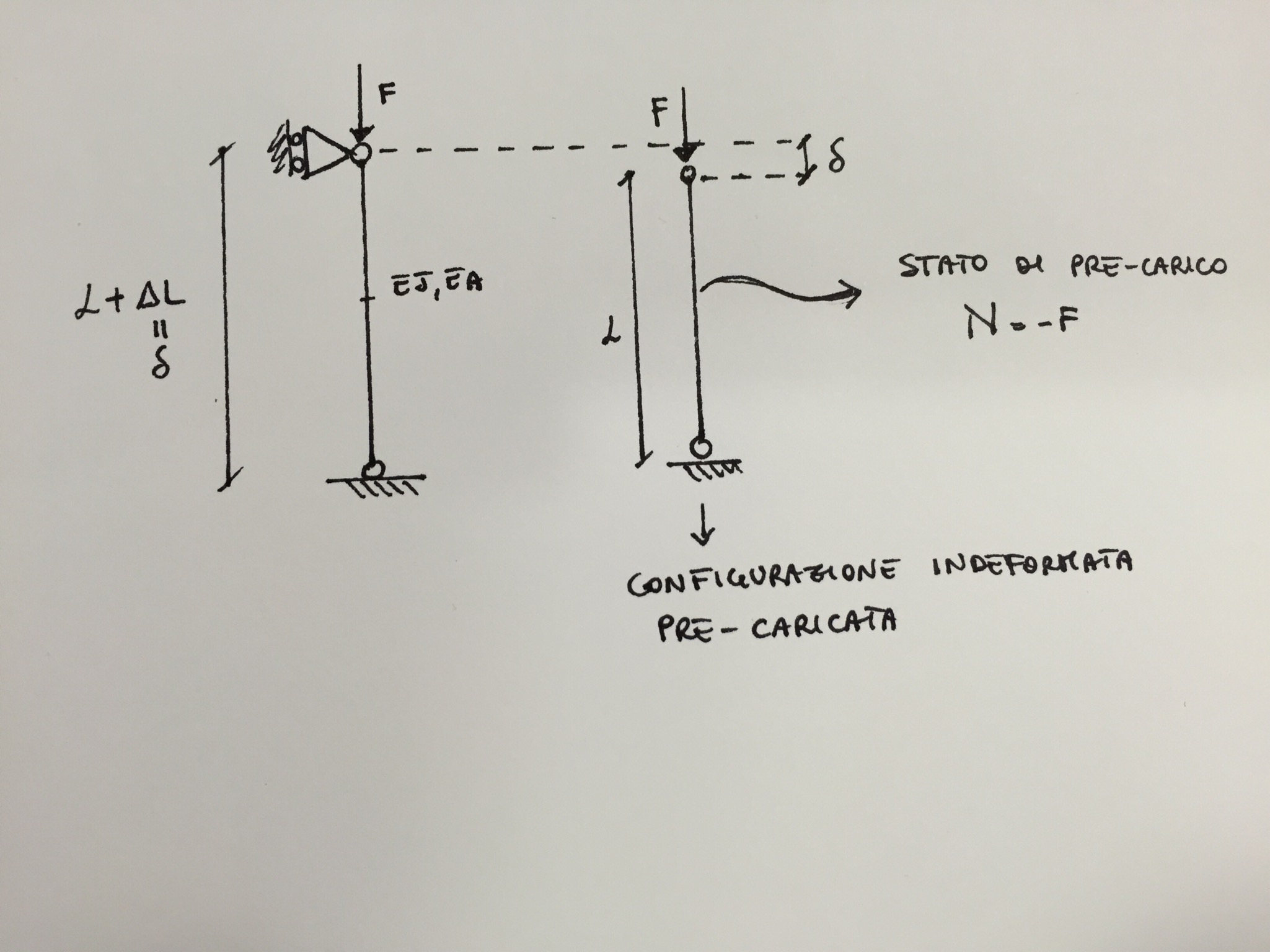
Lo stato di pre-carico è sforzo normale per una trave, se invece avessi una piastra o un solido avrei uno stato tensionale di pre-carico per ogni punto della struttura del tipo : $$ \begin{bmatrix} \sigma_x^0 \\ \sigma_y^0 \\ \sigma_z^0 \\ \tau_{xy}^0 \\ \tau_{xz}^0 \\ \tau_{yz}^0 \\ \end{bmatrix} $$
Quindi dato un sistema di carichi e vincoli (di cui alcuni potenzialmente non omogenei) carico la struttura per spostamento imposto, calcolo lo stato di pre-carico con un pre-calcolo lineare elastico e ottengo così uno stato tensionale $\underline{\sigma_0}$. Nel caso di un elemento “puntone” (o per trave alla Eulero) si riduce ad uno sforzo normale del tipo $N_0 = \sigma_0 A$.
Noto il pre-carico, devo calcolare la matrice di rigidezza geometrica $\underline{\underline{K_G}}$ associata a tale condizione di pre-carico. Come fare?
Calcolo il lavoro compiuto dal pre-carico quando deformo la struttura :

Una volta calcolato il lavoro è possibile passare ad una matrice i cui termini sono tutti proporzionali al pre-carico (perché si considera il pre-carico costante mentre la struttura si deforma, commettendo tuttavia un'approssimazione) e quindi ai carichi applicati.
Nota $\underline{\underline{K_G}}$ applico la procedura di estrazione della condizione di criticità annullando il determinante della matrice.
Tuttavia il metodo non risulta sempre valido. Vediamo qualche esempio:
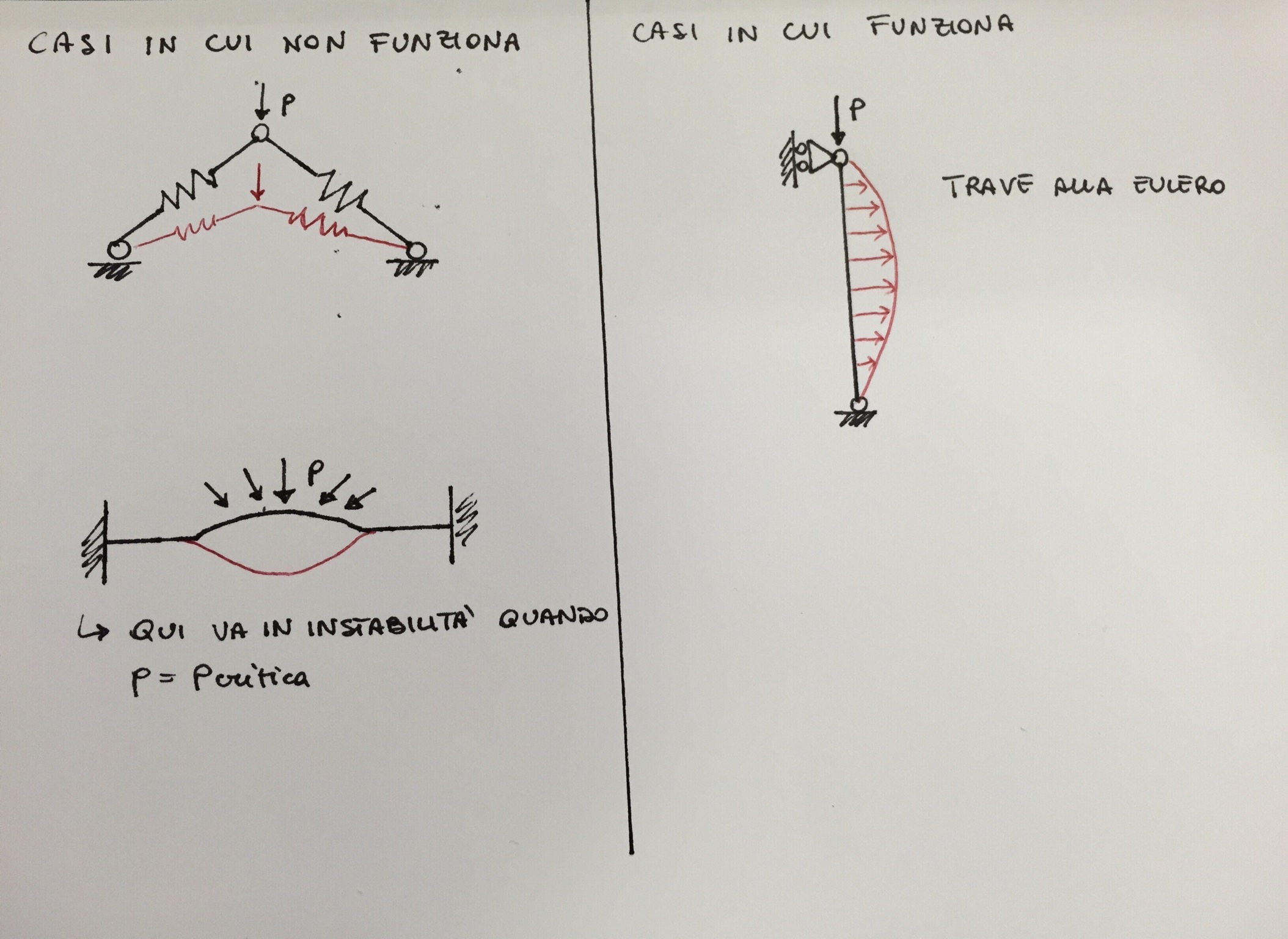
Noto che i modi di instabilità per la trave alla Eulero sono spostamenti trasversali al carico applicato, mentre negli altri due casi il modo di instabilità è dato da un abbassamento, ovvero è parallelo al carico applicato. In effetti se voglio che il metodo sia applicabile deve risultare che il prodotto scalare tra il vettore delle forze applicate $\underline{f}$ e l'autovettore associato al modo di instabilità $\hat{x_1}$ sia circa nullo:
$$ < \underline{f} , \hat{x_1} > \simeq 0 $$
In particolare nel caso della trave alla Eulero si potrebbe dire : $$ < \underline{f} , \hat{x_1} > = 0 $$ in quanto il carico è perfettamente ortogonale al modo di instabilità.
Ulteriori condizioni da rispettare affinché il metodo sia valido sono :
- vincoli da rispettare
- sistema di carico deve conservativo e statico
- perdita di instabilità su una biforcazione simmetrica (tanto può cedere verso destra tanto verso sinistra)
- deformazione pre-instabilità piccole
- materiale elastico
- effetto delle imperfezioni trascurabile
Tabella di monitoraggio carico orario
<hidden> Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Alessandro Franchini | 3 | — | — | — | |
| Baraldi Manuel | 3 | — | — | — | |
| Sanfilippo Andrea | 5 | — | — | — | 5 |
| Sparacino Simone | 5 | — | — | — | 5 |
| Revisore 1 | — | — | — | — | — |
| Revisore 2 | — | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | — | — | — | — | — |
