Indice
Instabilità in strutture complesse
Instabilità di travi perturbate
Consideriamo quattro travi in acciaio, incastrate ad una estremità e caricate con un carico di punta all’altra, di sezione circolare cava e con le seguenti caratteristiche geometriche:
- raggio medio, rm = 10 mm
- spessore di parete, t = 1 mm
- lunghezza, L = 1 m
Le travi sono tutte uguali a meno di una lieve perturbazione che coinvolge solo il terminale a cui è applicato il carico, che è deviato di una quantità ɛ.
(
Tale quantità è differente per ciascuna trave e, partendo dalla trave inferiore, vale:
- ɛ = 0.001 mm
- ɛ = 0.01 mm
- ɛ = 0.1 mm
- ɛ = 1 mm
Si fa notare che le strutture reali non sono perfettamente lineari quindi è facile che una trave “reale” presenti una perturbazione, forse non concentrata all’estremità come nel nostro caso studio, ma una perturbazione geometrica è sempre presente.
Si vuole applicare a queste travi dei carichi crescenti. Ci si aspetta che ci sia un carico critico, che vale:
$ _{P_{critico}}= \frac{\pi^{2} EJ}{(2L)^{2}} $
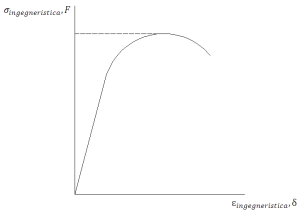
Un codice di calcolo farà fatica a lavorare quando il carico applicato raggiungerà il carico critico. Per ovviare a questa evenienza, si adotta la tecnica che sostanzialmente si usa nei test dei materiali. Si sa che la curva carico-spostamento relativa ad una prova a trazione su di un provino di materiale duttile presenta un andamento di questo tipo:
Dove:
- $ \sigma _{ingegneristica} = \frac{F}{A_{iniziale}} $;
- $ \varepsilon _{ingegneristica} = \frac{\delta}{L_{iniziale}} $.
Osservando la curva si comprende che se si procedesse ad una prova con controllo di carico (cioè con carico che aumenta nel tempo), non si riuscirebbe ad andare altre al valore indicato in figura con Fmax perché il provino non è in grado di stare in equilibrio sotto un carico di entità superiore a questo valore. Quindi, procedendo con una prova a trazione con controllo di carico è impossibile andare oltre un certo valore di F, che rappresenterà, quindi, un carico critico. La soluzione è procedere ad una prova con controllo di spostamento. Allora, anche nell’analisi FEM si utilizzerà un’analisi con controllo di spostamenti, perché si vuole andare a considerare anche il comportamento della struttura oltre le condizioni di instabilità, mantenendo fisso il carico ed aumentando gli spostamenti. Dunque nell’analisi FEM si procederà applicando uno spostamento imposto δ.
Finchè il sistema reagisce linearmente a compressione, c’è un legame semplice tra F e δ. In particolare si ha:
$ F=\sigma A=E\varepsilon A=E\frac{\delta }{L} A\Rightarrow \delta =\frac{FL}{EA} $
con:
- A: area della sezione retta del provino/trave;
- L: lunghezza iniziale del provino/trave.
Quindi, posso sfruttare questo legame per procedere con controllo di spostamento.
Implementiamo al Marc una bounrary condition del tipo fixed displacemt per creare il vincolo di incastro (a cui daremo il nome di clamp), nelle cui properties andremo ad attivare tutti gli spostamenti (‘displacement x, displacement y, displacement z) e tutte le rotazioni (rotation x, rotation y, rotation z).
Il percorso è:
boundary condition –> new –> structural –> fixed displacement;
properties –> selezionare tutti i displacement e le rotation.
Creiamo un’altra boundary condition per implementare il controllo di spostamento, che si comporterà come un carrello.
Andare a controllo di spostamento permette di sostenere la struttura, cioè il carrello creato per caricare la struttura finisce che la sostiene. Quindi, un’eventuale degenerazione della struttura in modo instabile viene evitato dall’effetto dello spostamento imposto che diviene un effetto di sostegno.
Applichiamo allora spostamenti crescenti. Poiché si tratta di un calcolo non lineare, un codice lineare non sarebbe in grado di cogliere un comportamento instabile. In Marc, per ottenere un’analisi per vedere un’instabilità occorre andare nel menu:
jobs –> properties –> analysis options –> advanced options
ed attivare large rotation.
Attivando invece large strain, si attiverebbero tutte le non linearità geometriche, che sono un oggetto molto complesso. Gli elementi strutturali non si modellano tipicamente in grandi deformazioni ma questo non toglie la possibilità di studiare non linearità geometriche dovute a grandi rotazioni.
Vediamo come reagisce la struttura aprendo al Marc il file dei risultati.
Osservazioni . Nelle strutture telaistiche si fanno calcoli:
- lineari, nel caso di verifica di rigidezze, di verifiche a fatica (il materiale non eccede ciclicamente lo snervamento, quindi tipicamente nelle analisi a fatica il materiale si comporta come lineare elastico);
- risposta in frequenza o estrazione modi propri (anche qui, l’ipotesi alla base è che il sistema sia lineare);
- simulazione di crash test, che sono non lineari di tipo esplicito, in cui le incognite non sono gli spostamenti ma le accelerazioni dei nodi. Il non lineare implicito (che è quello che stiamo studiando con questa analisi) tipicamente non si fa. Si usa il metodo non lineare implicito per simulare le deformazioni elasto-plastiche di un componente.
Nel caso di calcolo non lineare implicito si procede con una successione di istanti molto ravvicinati altrimenti la simulazione diverge. Infatti si va a considerare il disequilibrio su ogni grado di libertà della struttura. Se dividiamo il disequilibrio per la massa o l'inerzia del grado di libertà si ottiene l'accelerazione ed integrando questa nel tempo si trova la velocità degli spostamenti. Questa procedura si basa sulla legge di Newton. Più precisamente si pensa di procedere a controllo di carico, dove il carico è noto e gli spostamenti sono le incognite.
Si ipotizza di conoscere il comportamento della struttura:
se ho un valore del carico critico esiste il metodo delle tangenti o di Newton che a partire dalla stima iniziale, cioè la condizione di struttura scarica, mi permette in modo iterativo di avvicinarmi alla soluzione. Cioè data la forza riesco a trovare lo spostamento. Ma può capitare che il metodo possa non convergere perciò, invece di chiedere di passare dalla condizione di struttura scarica a quella carica in un solo passaggio, si preferisce parzializzare il carico per rendere più semplice il calcolo. Quindi per ogni passaggio intermedio si applica il metodo delle tangenti trovando per ciascuna la condizione di equilibrio. Se tutti i passaggi convergono si arriva al valore del carico critico altrimenti ci si accontenta di un valore inferiore.
Nella simulazione sono stati definiti dei livelli di carico in modo da raggiungere il 110% del carico critico. Analizzando i risultati si nota che appare la dicitura “tempo” la quale serve a modulare il carico cioè:
$ P(t)= P*t $
In realtà nel caso di calcolo statico (cioè se non ci sono forze inerziali e non ci sono reazioni viscose) serve:
- modulare il carico;
- definire a definire una dipendenza della struttura dalla sua storia.
Quindi per il nostro esercizio si ha che:
- per $t_{0}$ il sistema è scarico;
- per $t_{1}$ il sistema è caricato con $P_{critico}$;
- per $t_{2}$ il sistema è caricato con $P>P_{critico}$.
Mettendo a confronto la struttura deformata con quella originaria si nota che lo spostamento inizia ad essere più visibile nella trave più perturbata, mentre quelle meno perturbate si deformano di meno. Queste ultime colmano il ritardo quando il carico si avvicina al $P_{critico}$.
Analizzando la curva carico-spostamento si nota che:
- tutte le travi hanno una curva a tangente orizzontale per $P=P_{critico}$;
- la pendenza iniziale è la stessa per le 4 curve;
- la transizione è più isterica al calare della perturbazione.
Questo ci spiega perchè nel caso della piramide è stato introdotta la perturbazione, infatti in questo modo si riesce a rendere più continua l'evoluzione, cioè aiuta il solutore a seguire gli stati di equilibrio perchè sono più simili l'uno all'altro ed evita un andamento discontinuo delle curve. Inoltre le perturbazioni non variano l'entità del carico critico $P_{critico}$.
Per le analisi di strutture caricate fino al valore di instabilità si deve:
- procedere a controllo di spostamento;
- attivare le non linearità geometriche;
- introdurre una piccola perturbazione.
altrimenti il passaggio da soluzione lineare elastica a struttura instabile è troppo repentino. Infatti se si toglie la non linearità, disattivando large rotation, e si rilancia il calcolo si ha che la struttura non si muove sotto carico e la curva Forza-Spostamento è una retta.
Piramide
Piramide buckling base nella forma perturbata e rinforzo della struttura con tiranti
Consideriamo una piramide (file: piramide_buckling_base.mfd ) alla quale abbiamo applicato un carico di 1000 N sul vertice: risolvendo la struttura con analisi di buckling si noti che il primo moto instabile avviene 8,46 volte questo carico. Volendo aumentare il carico critico sopportabile dobbiamo attuare un rinforzo della piramide, di conseguenza, osservando la deformazione ci si chiede come ritardarla o impedirla.
Considerando i nodi del montante a metà altezza della piramide, si può osservare che fra questi e i vertici della base avviene una deformazione quadrilatera: si potrebbe impedire inserendo tiranti e puntoni sulle diagonali in sezione ridotta rispetto ai montanti con successivo aumento di massa inevitabile (file:piramide_buckling_neotiranti.mfd).

A questo punto procediamo con un nuovo calcolo nel quale ritroviamo un carico critico di circa 12,67 volte i 1000 N applicati alla struttura. Questo risultato ci dimostra che i fenomeni di instabilià si palesano ad un carico più grande del 50% rispetto al precedente.
In realtà fra i due rinforzi inseriti solo uno sarà instabile in questo punto,vale a dire quello soggetto a compressione, mentre il tirante sottoposto a trazione avrà ancora la possibilità di rinforzare la struttura; quanto potrà durare ancora?
Per poter avere questa informazione bisogna necessariamente effettuare una simulazione non lineare detta di post-buckling o post-instabilità.Si potrebbe optare per una simulazione non lineare di spostamento: si applica uno spostamento imposto finchè la soluzione converge ma ad un certo punto, precisamente all'incremento 70 dove la struttura diventa labile (matrice singolare,codice 2004).
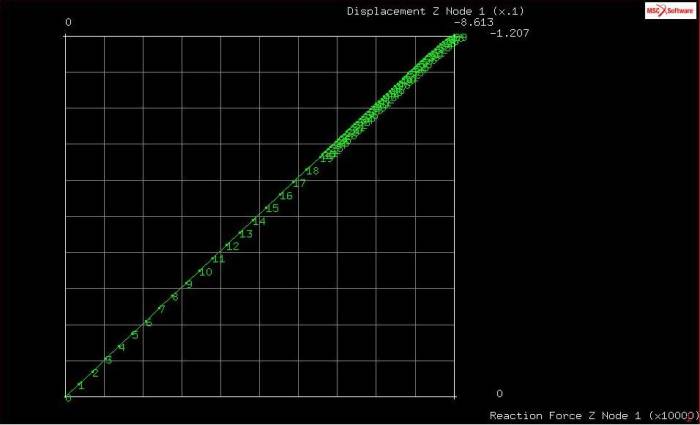
La labilità del sistema non è dovuta all'assenza di un vincolo imposto bensì alla presenza di un moto d'instabilità. Quindi selezionando History plot-set locations e inserendo il punto di apice raccolgo i dati in un grafico spostamento (direzione z) in ascissa e carico (reazione vincolare direzione z, non ci sono forze applicate) in ordinata.
Si noti che il sistema evolve linearmente fino ad un punto corrispondente a 8 decimi di mm e 12070 N.
Ricordando che il carico critico precedentemente ricavato era di circa 12700 N, possiamo dire che è stata raggiunta l'instabilità prima di questo.
Il risultato ottenuto non ci dà informazioni su cosa succede oltre la raggiunta instabilità di una delle due travi e quindi in questa maniera non si ha la possibilità di procedere con l'analisi.
Per far avanzare l'algoritmo viene selezionato un comando all'interno del menù load cases che impone il proseguimento del calcolo anche nel sistema labile, e ignora la non convergenza della soluzione. Da un punto di vista grafico si può notare che la struttura perde fisicità a carichi maggiori fino a collassare intorno all'incremento 105: visualizzando le stesse informazioni su un grafico spostamento carico ritroviamo che oltre il carico critico di 12070 N la curva decresce.
In conclusione possiamo dire che nella struttura piramidale con rinforzi diagonali il carico di 12070 N rappresenta il massimo della sollecitazione sopportabile.
Rinforzo con pannelli
Adesso proviamo a vedere quando si manifesta instabilità in una struttura piramidale con rinforzo a pannelli. Inseriamo sulle facce dei pannelli (si consiglia di effettuare un offset di questi in maniera da non posizionarli a cavallo delle travi, ma, come dovrebbe essere nella realtà, all'esterno o all'interno di queste senza compenetrarle) scegliendo, come materiale di rinforzo, l'alluminio. Dopo aver saldato i pannelli ai tiranti col collasso nodale (comando sweep), si effettua un calcolo di instabilità della nuova configurazione, individuando nei risultati un modo di instabilità a compressione dei pannelli per un carico di 3500 N (i pannelli vanno in instabilità a 3500 N mentre la struttura portante regge fino al carico precedentemente trovato). I pannelli sono in grado di bloccare la deformazione a quadrilatero della parte bassa delle facce triangolari, e ci si aspetta che anche con un carico di 8000 N la struttura non vada in crisi (in quanto le travi sotto i pannelli non sono indebolite dai pannelli). Dopo i 3500 N la soluzione elastica perde significato, e per ottenere dei risultati oltre questo carico è necessario effettuare un'analisi non lineare, che mi verifica come sostanzialmente non ci sono deformazioni sui fianchi delle travi nonostante alcuni spostamenti dei pannelli (in instabilità). Si valuta il livello di carico: open post file –> history plot –> set locations e si aggiungono le curve per tutte le locazioni (spostamenzo z in ascissa, reaction force z in ordinata), vedendo che la struttura raggiunge senza particolari problemi circa 31400 N di reaction force (cioè a fine corsa del pistone comprimente non si è ancora raggiunta l'instabilità). Il comportamento dei pannelli è differente da quello dei puntoni: infatti se il puntone va in instabilità e non irrigidisce la struttura può essere “eliminato” dalla struttura stessa; al contrario un pannello può andare in instabilità a compressione irrigidendo a taglio, e questa situazione non è traumatica per la struttura se si vogliono individuare i carichi critici (aumentando lo spostamento imposto si deve effettivamente vedere instabilità della struttura). Per strutture pannellate con tiranti e puntoni è importante notare come raggiungere l'instabilità non equivalga a perdere la struttura: infatti attraverso il calcolo di linearized prebuckling si può valutare velocemente il carico limite che può sopportare la struttura, sapendo che per soluzioni lineari il carico critico individuato può non coincidere col carico critico effettivo della struttura (valutabile attraverso un'analisi non lineare, fino a quando il solutore lo permette).
Non linearità di un sistema
Le fonti di non linearità:
- definiscono il limite del solutore (se lineare)
- non possono essere inserite in analisi modali o in frequenza
- si manifestano per grandi rotazioni (cioè quando senϑ ≠ ϑ e cosϑ ≠ 1) e per grandi deformazioni (ad esempio in prove di trazione quando la sezione iniziale non è rappresentativa della sezione istantanea, cioè quando εx ≠ du/dx)
Esistono tre tipi di non linearità:
- non linearità geometrica: non si trova facilmente in un telaio (alluminio e acciaio cedono prima di arrivare a grandi deformazioni, la si ritrova solo per elementi in gomma)
- non linearità di materiale: materiale non lineare, fenomeni di creep, plasticizzazione o elasticità non lineare (come accade per le gomme)
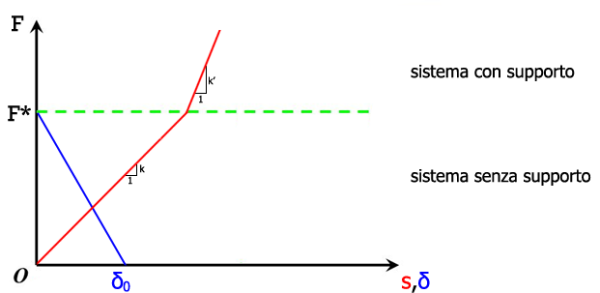
- fenomeni di contatto monolatero: si consideri un corpo senza attrito (ad esempio una trave incastrata con carico traverso in estremità) e un oggetto sottostante con gioco iniziale pari a δ (condizione iniziale F=0), e sia s il cedimento sotto il punto di applicazione della forza F. Esiste un carico F* per il quale la trave sfiora la superficie dell'oggetto sottostante: disegnando una curva s(F), si avrà che l'andamento della stessa sarà pari a quello libero fino a quando non avviene il contatto. Allo stesso modo si può plottare il grafico δ(F): quando F=0 δ sarà pari al gioco iniziale, poi calerà linearmente fino ad annullarsi e da lì in poi resta nullo all'aumentare della forza F. La non linearità si ha anche in assenza di gioco: in questo caso la transizione è nell'intorno dello zero. Il diagramma s(F) ha due diverse pendenze: 1-k' con rigidezza propria del sistema supportato, 1-k con rigidezza del sistema senza supporto (quando il carico varia di segno).
Autori
Michele De Luca Matr. 104899
Matteo Notarianni Matr. 99717
Francesco Davide Di Lorenzo Matr.106218
Leonardo Mastromauro 105214
Tabella di monitoraggio carico orario
Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| De Luca | 4 | — | — | — | — |
| Notarianni | 4 | — | — | — | — |
| Di Lorenzo | 4 | — | — | — | — |
| Mastromauro | 4 | — | — | — | — |
| Revisore 1 | — | — | — | — | — |
| Revisore 2 | — | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | — | — | — | — | — |
Materiale caricato dal Docente
instabilità travi perturbate; l=1000 mm, sezione circolare rm=10mm, spessore di parete 1mm, acciaio.
piramide_buckling_base.mfd piramide_buckling_neotiranti.mfd piramide_buckling_neopannelli.mfd