Indice
Seminario Marco Di Cecco, Ferrari GES, a tema Rigidezze Veicolo
RIGIDEZZE VEICOLO
Con lo studio delle rigidezze del veicolo viene costruito un modello agli elementi finiti (FEM) K da poter implementare al simulatore da far provare ai piloti, nonché per la costruzione della macchina. Si hanno dei target da raggiungere in termini di rigidezze. Il ciclo di progettazione dura circa 2 settimane e viene fatto circa 20 volte l’anno, ma sul simulatore vengono caricate solo 3 versioni definitive.
Il progetto viene deciso dal CHIEF DESIGNER, che dice per esempio “quest’anno vogliamo aumentare del 20% la rigidezza del veicolo a CAMBER (angolo di campanatura), con che aumento di peso è possibile questa modifica (target)?”
POSSIBILI TARGET DI IMPOSTAZIONE VEICOLO
- Camber;
- Toe (convergenza);
- Rigidezza verticale: applicando un carico verticale alla ruota vedo di quanto il CONTACT PATCH (area di contatto ruota-suolo) diminuisce;
- Rigidezza del telaio: lo vedo come trave incastrata, applico un carico laterale alla ruota, e valuto lo spostamento. La rigidezza è il rapporto tra forza e spostamento;
- Ridurre al minimo la massa: senza lavorare sulle rigidezze, trovare il compromesso di minima massa dell’intero veicolo.
Tutti questi target hanno lo scopo di far lavorare al meglio gli pneumatici, ovvero trovare le massime forze agenti tra pneumatico e suolo.
ANALISI SOSPENSIONI
Ma come si fa? Per primo si guarda la cinematica delle sospensioni. Ad ogni scuotimento sono legate delle variazioni degli angoli:
- Camber gain
- Bump steer: di quanto sterza la ruota sotto l’effetto dello scuotimento (solo dovuto alla cinematica)
- Caster change
- Kingpin
In particolare il guadagno del camber, ovvero quanto ne riesco a recuperare con lo scuotimento, viene determinata per avere la ruota esterna, nelle curve ad alta velocità con macchina rollata, con meno camber possibile (quasi verticale) per migliorare le forze a terra e farla lavorare al meglio. In realtà questo procedimento si fa per avere tutte e quattro le ruote che lavorano al meglio, per ottenere la massima prestazione del veicolo.
VEDIAMO I GRAFICI
I grafici derivano dalla telemetria di una curva specifica, porzione di pista in rosso. Nella prima immagine in alto la linea azzurra rappresenta la velocità, quella arancione il segnale del pedale del freno. Nel grafico sotto: curva blu accelerazione longitudinale, curva rossa accelerazione trasversale, che quando è diversa da zero ci dice che siamo in curva, altrimenti rettilineo. Quelli di sinistra rappresentano le variazioni di camber e toe della ruota sx, quelli a destra della ruota dx
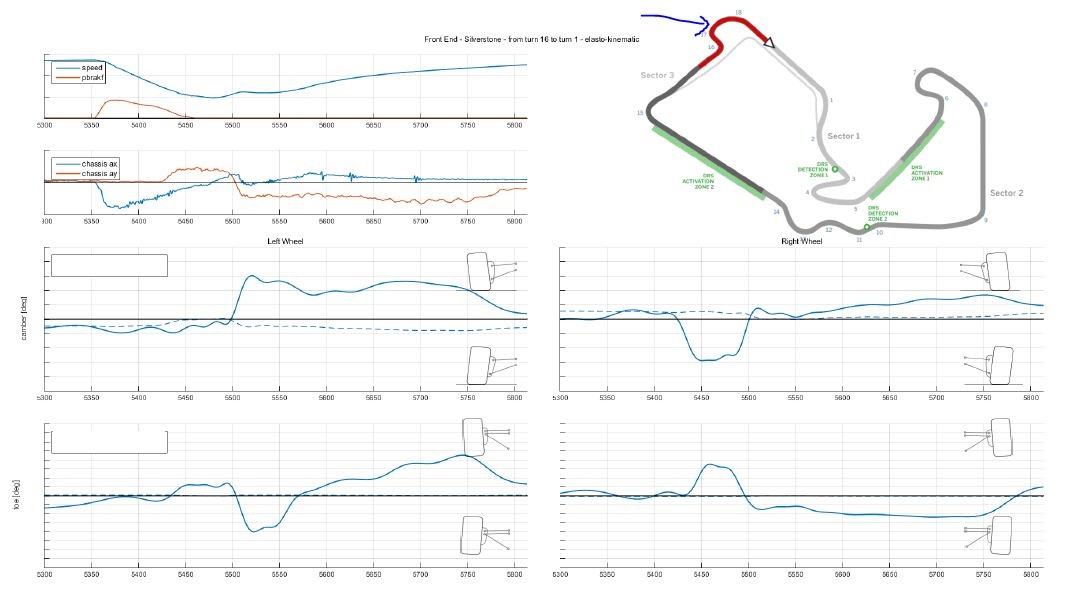
I valori dei grafici sono scalati, le variazioni reali degli angoli sono dell’ordine dei decimi di grado, paragonabili alla variazione di setup che si possono fare in pista. Le linee tratteggiate rappresentano la variazione dell’angolo derivante dalla sola cinematica delle sospensioni, quindi il valore che vorremmo ottenere in quelle date condizioni. Invece, come si vede dalla linea continua, dovuta alle cedevolezze, il camber che otteniamo è molto più alto in curva, perché il veicolo non è infinitamente rigido. Questo ci dice che le rigidezze/cedevolezze sono molto importanti per valutare il guadagno di camber e quindi per il comportamento in pista del veicolo, più della sola cinematica. Tutto ciò viene studiato al FEM, come in questo caso, oppure tramite un banco prova che simula una curva applicando dei carici alle ruote tramite dei bracci meccanici.
Quindi ridurre del 20% la variazione a camber del veicolo significa ridurre del 20% la differenza tra le due curve che si vedono nel grafico, che viene generata dalle forze a terra del pneumatico. Le forze e i momenti che sono applicati al punto a terra della ruota sono $F_{x}$, $F_{y}$, $F_{z}$ ed $M_{z}$, momento di torsione con asse perpendicolare al suolo, generato dall’angolo di deriva e dalla distribuzione delle forze a terra. Se sposto le forze e il momento al centro ruota, avrò dei momenti di trasporto. Per esempio per la $F_{y}$ si genera un momento positivo $$M_{x}=F_{y}\ast LR$$ ($LR$=Loaded Radius). Quindi avrò 6 componenti (3 forze, 3 momenti) al centro ruota.


Nel punto di massima frenata avrò la componente $F_{x}$, $F_{z}$ molto grandi, $F_{y}$ e $M_{z}$ molto piccoli perché non sto sterzando; in più avrò i momenti di trasporto, ovviamente legati alle forze, $M_{y}$ molto grande e $M_{x}$ molto piccolo. Queste forze creano delle deformazioni nello pneumatico che saranno diverse in curva con le ruote sterzate, dove $F_{x}$ è praticamente nullo ed $M_{y}$ sarà molto basso perché ho la forza invertita, $F_{y}$, $M_{x}$ ed $M_{z}$ molto alti; tutte queste hanno effetti sul camber, aumentandolo.
Quindi diminuire del 20% la cedevolezza significa controllarla in tutti e sei i g.d.l. Perciò, prendendo in considerazione il modello FEM dell’intero veicolo, andiamo a vedere, applicando i carichi unitari alla matrice di rigidezza, cosa succede al camber (vedi grafico con barre bianche); inoltre, diamo come input alla matrice i valori ottenuti dalla telemetria ottenendo il grafico a barre verdi, che rappresenta le variazioni reali di camber nel tratto di pista considerato, derivanti dai vari contributi.
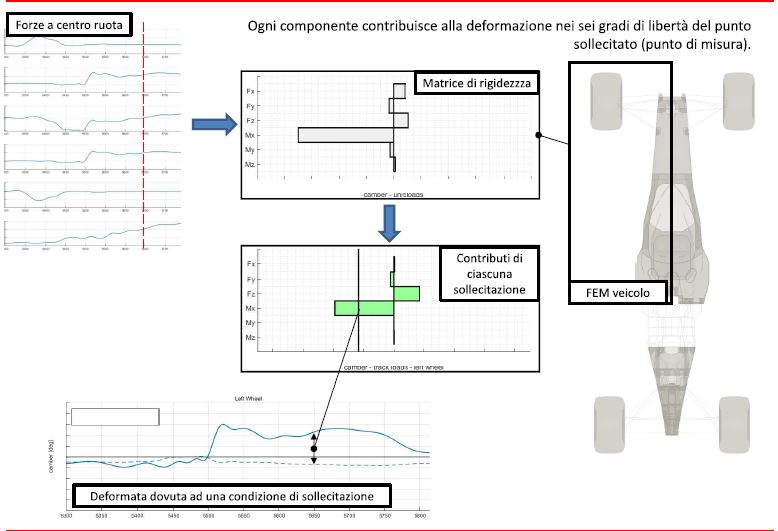
Nell’esempio si vede che $M_{x}$ è quello con il contributo maggiore, ma anche $F_{z}$ è importante, soprattutto se valutiamo la ruota interna, sollecitata dal carico aerodinamico. Trascurando $F_{y}$, $M_{x}$ tende a far ridurre il camber, mentre $M_{z}$ tende a recuperarlo un po' e il risultato è il valore che si riscontra nel grafico. L’algoritmo da seguire è il seguente:
INPUT: forze agenti sul centro ruota (in questo caso derivanti dalla telemetria) → si danno in pasto alla matrice di rigidezza (dipende dal modello dell’intero veicolo) → si vede come cambia il camber sotto l’effetto di ogni singola componente, valutandone i contributi.
Si definisce la rigidezza a camber come $$K_{camber}=\frac{\partial F_{y}}{\partial \beta}$$ dove $\beta$ è l’angolo di camber.
Ma nella realtà le cose sono molto più complesse, perché la variazione di forza $\partial F_{y}$ dipende da tutte e sei le componenti, che variano nei diversi punti del tracciato in caso di rettilineo, dove è più importante la $F_{z}$, dovuta al carico aerodinamico, o di curva.
Se invece valutiamo l’angolo di toe, quindi di sterzatura elastica, si avranno contributi molto più complessi. Ce ne sono due che hanno la stessa entità ed altri tre minori, ma comunque importanti. Nei carichi unitari si vede che ci sono più carichi rilevanti rispetto al caso del camber.
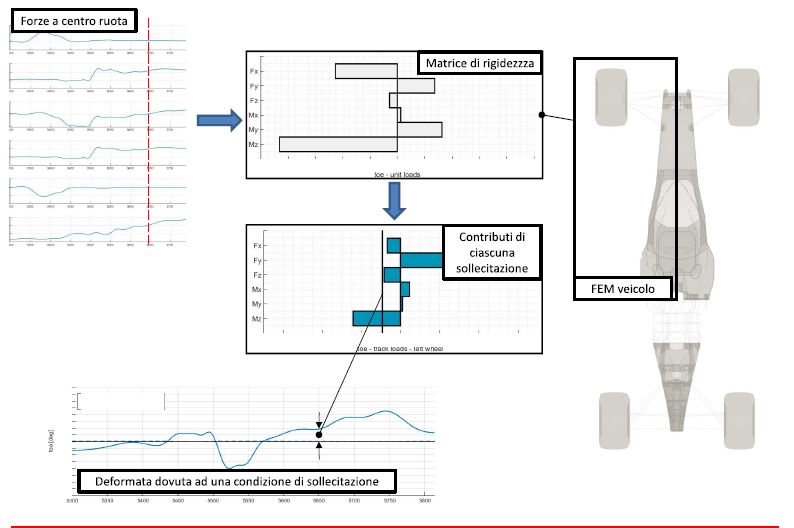
Se ci chiedessero di aumentare la rigidezza a toe le cose si complicherebbero, una soluzione potrebbe essere aggiungere peso in un elemento del veicolo per migliorare le cose in un dato punto del circuito, però rischiando di avere condizioni sfavorevoli in altri settori.
Riassumendo:
- La cinematica viene definita per sfruttare al meglio gli pneumatici;
- Le cedevolezze modificano sostanzialmente le caratteristiche della cinematica;
- Il valore assoluto degli angoli del gruppo ruota dipende dalle 6 componenti di forze e momenti.
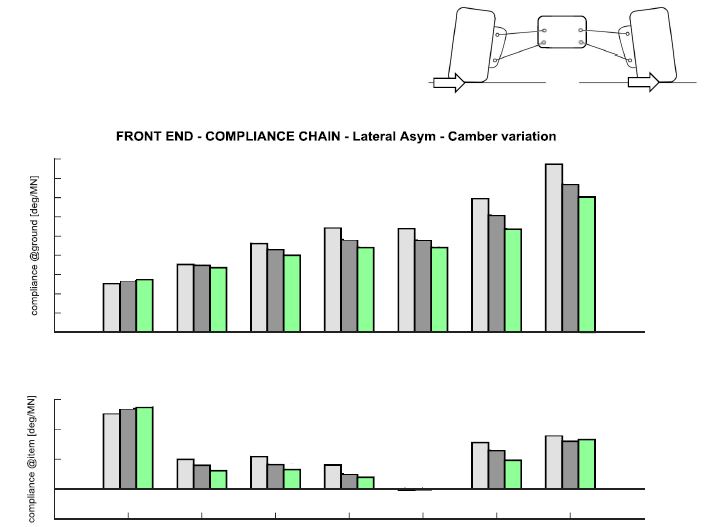
Per cui se vogliamo aumentare la rigidezza a camber non ci basta modificare il rapporto $$K_{camber}=\frac{\partial F_{y}}{\partial \beta}.$$ Una volta scelti i componenti su cui agire per cambiare la rigidezza a camber del veicolo, cerco il modo che mi faccia trovare l’ottimo tra minima massa aggiunta e aumento di rigidezza. Si prende in considerazione il front-end (assieme del telaio anteriore con le sospensioni e i due gruppi ruota anteriori), in caso di rigidezza verticale viene caricato da una forza verticale e si va a vedere di quanto si alzano le ruote da terra. Si nota che, se voglio aumentare la rigidezza, mi conviene lavorare sul telaio (ultimo gruppo di valori nel grafico in basso), che ha il contributo maggiore, seguito da sospensioni (3° gruppo), ruota (1°) e sospensioni interne, dette in-board, composto da rocker, molle ecc (5°). Il grafico sopra rappresenta la sommatoria dei vari contributi del grafico in basso.
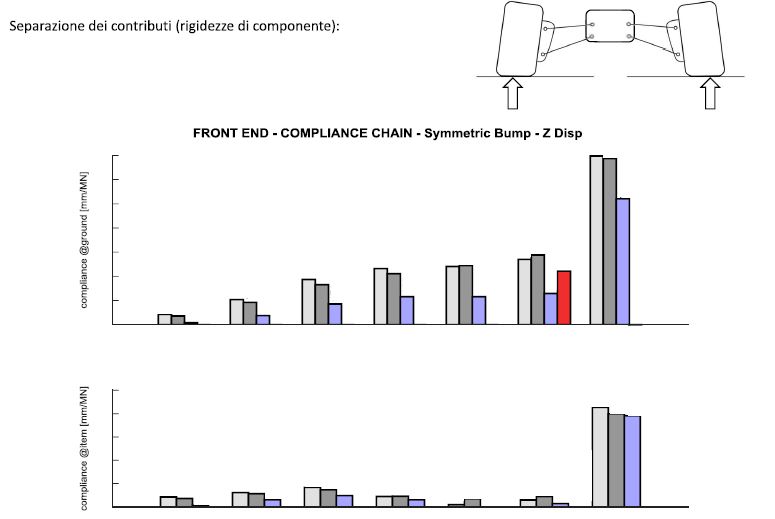
Invece, nel caso di rigidezza laterale il contributo più importante viene dato dal gruppo ruota, anche se il telaio rimane rilevante. Ma in questo caso, lavorando sul telaio, aggiungerei molto peso inutilmente, in quanto me ne servirebbe molto meno nel gruppo ruota per raggiungere lo stesso target.
CINEMATICA
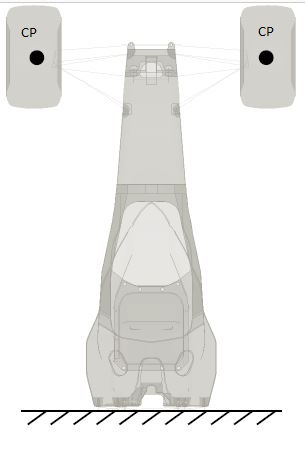
Si fa un’analisi di posizione trovando le posizioni di tutti gli elementi delle sospensioni, tramite l’algoritmo delle tre sfere. Come input si inserisce solo lo scuotimento e NON le forze. Questo è sufficiente per trovare le variazioni degli angoli del gruppo ruota e quindi disegnare i grafici appena visti.
Alla cinematica si aggiunge la parte di deformazione elastica, studiata tramite la modellazione FEM. Però un modello completo del veicolo è molto pesante, considerando che il telaio ha circa 300 000 nodi ed un solo gruppo ruota circa 1 milione, quindi 6*1 000 000=6 000 000 di g.d.l. (ci vogliono ore per simularlo). Per risolvere questo problema di calcolo faccio una riduzione della matrice di rigidezza. Per esempio prendendo in considerazione il front-end (circa 2 300 000 nodi), di cui mi interessano gli spostamenti del CP (Contact Patch) della ruota sx, elimino dal calcolo tutti gli altri elementi e riduco il sistema a 6 g.d.l. con input le forze applicate al CP oppure al centro ruota, con i relativi momenti di trasporto, e vedo in uscita gli spostamenti del punto interessato. In questo modo avrò bisogno solo di una matrice (2*6)x(2*6) invece che di una matrice (6n)x(6n), con n= 2 300 000. La relazione che si risolve è semplicemente $$F=K\ast u$$.
Dato che a me serve il vettore degli spostamenti u e dovrei invertire la matrice K, lavoro direttamente con la matrice inversa C, detta matrice delle cedevolezze. Questa sarà il mio modello K. Siamo sempre nel campo lineare, quindi la matrice di cedevolezza non cambia a seconda delle forze che gli applico, perciò è costante in tutto il tracciato. In questo modo ho ridotto moltissimo i tempi di calcolo della simulazione. L’importante è fare un modello completo molto vicino alla realtà, in modo tale che anche quello ridotto dia dei risultati paragonabili con le prove sperimentali, dato che nel passaggio tra un modello e l’altro non commetto errori di approssimazione. Una volta ridotto il sistema posso dargli come input i dati della telemetria, da cui ottengo le deformazioni nel punto a terra, in tutto il tracciato, a cui sommo i dati del modello della cinematica. Da queste derivo i valori assoluti degli angoli relativi al mio modello.
SEPARAZIONE DEI CONTRIBUTI
Una volta che ho la curva del camber devo vedere come aumentarla e quindi su quali contributi andare a lavorare. Li studio tutti separati, come prima, in modo da isolare quelli più rilevanti. Potrei anche aumentare la cedevolezza di qualche componente per avere più guadagno del camber in qualche parte della pista, avendo dalla mia parte una riduzione del peso, rischiando però di diminuire guadagno di camber in altre. Questo perché ogni volta che aumento la rigidezza del gruppo ruota del 20% ho un aumento di circa 1 kg (in più ho problemi di masse non sospese). Per aumentare la rigidezza dove vado a posizionare la massa in più? Devo controllare i soliti contributi di ogni elemento del veicolo. Prendo il modello completo del front-end e lo vincolo in vari modi così da trovare i contributi singolarmente. Si parte dalla ruota e arrivo al modello completo (ad esempio: gruppo ruota → ruota + sospensioni → metà front-end → modello completo) invece, se parto dal modello completo e arrivo alla ruota sottrarrò tutte le volte i contributi successivi. In questo modo ho una cedevolezza sempre più grande di modello. Dal grafico si nota che i contributi maggiori sono quelli del gruppo ruota e del telaio (diviso in due), quindi la cosa migliore è lavorare sul telaio, che essendo in materiale composito mi da la possibilità di aggiungere poco peso ed avere un incremento rilevante di rigidezza.

ASSEMBLAGGIO MATRICE DI RIGIDEZZA
Una volta deciso dove lavorare, devo ottimizzare. Supponiamo di aver scelto il gruppo ruota (di solito non si fa perché significa aggiungere molto peso), quindi lavorerò sul cerchio.
Attuerò un’ottimizzazione topologica → reingegnerizzazione della soluzione → ottengo il mio modello ottimizzato e infine lo vado a sostituire nel modello del front-end. Se i risultati sono soddisfacenti ridurrò il modello in C e avvierò la simulazione.
Questo processo di ottimizzazione dura circa una settimana, è quindi impossibile fare tutto in due. Un metodo per ridurre i tempi è quello di ridurre la matrice K generale in tante sottomatrici, per il front-end sono 11, rappresentano i singoli componenti del modello:
- 2 per le ruote, 1 a gruppo ruota;
- 4 per gli wishbone, 2 a dx e 2 a sx;
- 2 per i pull-rod, 1 a dx e 1 a sx;
- 2 per i track-rod (tirante convergenza), 1 a dx e 1 a sx;
- 1 per il telaio.
Così, modificandone una ad una, è più semplice variare la matrice grande senza dover aspettare il modello ottimizzato completo; riducendo così i tempi di progettazione da giorni a qualche minuto. Questo metodo è applicabile all’intero veicolo, non è altro che un modello FEM ridotto.
Ad esempio, se si prende la sottomatrice di un track-rod, che lo si può schematizzare come una barra di rigidezza $$K=\frac{A\ast E}{L} $$ in base ad un aumento della rigidezza costruisco la relativa sottomatrice $K_{trod}$, che vado a rimettere nel “matricione” sostituendo quella vecchia ed effettuando l’assemblaggio. Posso fare così per ogni elemento del modello. Tra gruppo ruota e track-rod ci sono i giunti, sono gli elementi più cedevoli dell’assieme, a causa delle caratteristiche geometriche (fori per alloggio vite), e delle tolleranze di montaggio, quindi sono difficili da modellare. Per questo si simulano con una molla con rigidezza nominale derivante dai risultati sperimentali dei giunti.
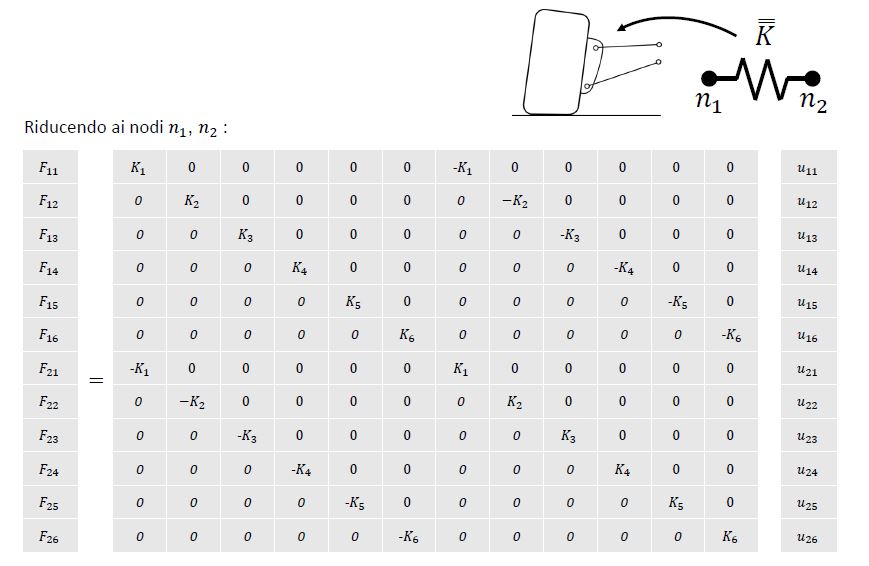
Si vincola la molla ad un estremo (nodo 2, n2) e si applica una forza all’altro (nodo 1, n1), e si scrive una matrice di rigidezza del giunto. Se guardiamo n1 possiamo scrivere che la componente assiale della forza sia pari a $$F_{1}=k_{11}\ast u_{1,1}+k_{22}\ast u_{2,1}+...+k_{66}\ast u_{6,1}.$$ Se svincoliamo la componente assiale da tutte le altre componenti e facciamo la stessa cosa con tutte le altre componenti (ovvero $F_{1}$ agisce solo su $u_{1}$, $F_{2}$ su $u_{2}$ ecc), otteniamo una matrice diagonale con presenti solo $k_{11}$=$k_{1}$, $k_{2}$, …, $k_{6}$. Così ho svincolato tutte le forze dalle direzioni su cui non agiscono.
Se adesso vincolo la molla in n1 e applico la forza ad n2 otterrò $$F_{2}=k_{11}\ast u_{1,2}+k_{22}\ast u_{2,2}+...+k_{66}\ast u_{6,2},$$ facendo lo stesso ragionamento di prima otterrò la solita matrice con $k_{1}$, $k_{2}$, …, $k_{6}$.
Applicando l’equilibrio alla molla sottoposta ad entrambe le forze otterrò $$ F_{1}=F_{2} → F_{1}-F_{2}=0 → k_{1}\ast u_{1}-k_{1}\ast u_{2}=0,$$ perciò nella matrice avrò i coefficienti relativi al nodo2 negativi, adesso la posso scrivere intera. Sarà una matrice diagonale.
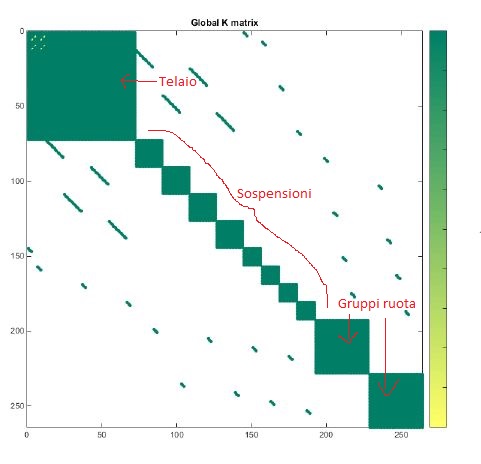
Applicando questo algoritmo a tutti i giunti del veicolo ottengo le matrici di tutti i componenti. Per i due gruppi ruota del front-end avrò 20 giunti (12 attacchi al telaio, 6 a dx e 6 sx, e 4 attacchi per ogni ruota). In tutti i nodi in cui arrivano più elementi, vanno sommati tutti i loro contributi; una volta scritte tutte le matrici possiamo passare all’assemblaggio di quella del veicolo che avrà elementi sulla diagonale e qualcuno fuori diagonale, sarà simmetrica. Le varie sottomatrici non hanno elementi comuni, gli elementi dei vari componenti appartengono solo ai relativi componenti, l’unico collegamento che esiste tra questi sono le matrici dei giunti, fuori diagonale, che per esempio collegano quelle delle sospensioni a quelle dei gruppi ruota. In questo modo ho effettuato l’assemblaggio di tutte le matrici ottenendo una matrice ancora troppo grande da simulare, quindi la riduco nuovamente ai punti a terra, ottenendo una matrice 12×12 da utilizzare per la simulazione di telemetria. In questo modo i loop di sviluppo della macchina sono molto rapidi e permettono di stabilire dei target, non solo di inseguirli.
Esistono anche modelli non lineari di giunto, ad esempio giunti con gioco, che cambia il comportamento della molla fittizia, che avrà una rigidezza diversa; in questo caso dovrò far variare la matrice di rigidezza del giunto per tutta la telemetria, a seconda della forza che passa sul giunto, seguendo la curva della rigidezza equivalente, detta secante. Questa non linearità mi permette di introdurre nella modellazione anche dei giochi simulati e delle cedevolezze non lineari. Quindi posso fare molte simulazioni diverse in poco tempo.

Questo studio viene effettuato generalmente su un massimo di 3 circuiti:
- Montecarlo, perché è un circuito molto lento dove è molto importante la trazione;
- Barcellona, dove sono presenti curve ad alta velocità di percorrenza, dove la trazione è meno importante
- Silverstone, stesso motivo di Montmelò.
È molto difficile che venga effettuato durante la stagione per la macchina che corre, ma per lo più sul prototipo dell’anno successivo, perché cambiare le cose in corso d’opera ha costi elevatissimi, nonché tempi di realizzazione molto lunghi, in quanto alcuni pezzi devono superare tutte le normative, compresi i crash test (come il telaio).
Autori
Capone Gabriele
Copponi Giorgio
Solimeno Luca
Salvatore Lamanna
Fabio Santi Mortellaro

Discussione
REVISORE 1
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
No.
Il testo proposto è coerente con gli appunti personali del revisore?
Sì.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
No.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Sì.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
No.
Ore dedicate a questa revisione
1/2 h
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
La lezione è stata riportata in maniera chiara e completa. L'unica correzione che farei, riguarda il paragrafo “Assemblaggio della matrice di rigidezza”, nel quale dopo la formula K=A*E/L è presente una virgola all'inizio del capoverso, ma nel complesso il testo risulta scorrevole.
Il testo proposto è coerente con gli appunti personali del revisore?
Si.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
No.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Si, gli appunti sono sufficienti.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
Non è necessario.
Ore dedicate a questa revisione
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
il testo è abbastanza fruibile
Il testo proposto è coerente con gli appunti personali del revisore?
sì
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
no, le immagini abbondano
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
sì
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
no