Indice
Pesi e punti di campionamento quadratura gaussiana a 2 punti
QUADRILATERO ISOPARAMETRICO 4 NODI (PARTE 2)
$ U=\frac{1}{2}\delta^{T}[t\iint_{a}B^{T}(\xi,\eta)DB(\xi,\eta)]\delta $
$ K=t\iint_{-1}^{1}B^{T}(\xi,\eta)DB(\xi,\eta)\left | J(\xi,\eta) \right |d\xi d\eta $
Questo integrale fornisce la matrice di rigidezza.
Dobbiamo integrare :
$ \iint_{-1}^{1}F(\xi,\eta)d\xi d\eta=K $ con:
$ F(\xi,\eta)=B^{T}(\xi,\eta)DB(\xi,\eta)\left | J(\xi,\eta) \right | $
L’integrale non si svolge in forma esatta; si utilizza una formula di stima: $ \int_{-1}^{1}g(\zeta)d\zeta $
E’ usata per elementi non distorti,cioè con $ \left | J(\xi,\eta) \right |=cost $
PROCEDURA DI QUADRATURA GAUSSIANA
Prevede il campionamento della funzione in un numero finito di punti. Questa procedura è esatta per alcune famiglie di funzioni; nel nostro caso è esatta per i polinomi:
$ quad=\sum_{i=1}^{N}w_{i}F(\zeta_{i})\simeq \int_{-1}^{1}g(\zeta)d\zeta $
dove $w_{i}$ sono i pesi, N è un numero di punti a piacere e $F(\zeta_{i})$ è il campionamento specifico della funzione nel punto i.
Per N=2 si ha $ quad=w_{1}F(\zeta_{1})+w_{2}F(\zeta_{2}) $
Definita questa formula rimangono 4 gradi di libertà $(w_{1},w_{2},\zeta_{1},\zeta_{2})$. Per definire i 4 gradi di libertà, dobbiamo dunque trovare un ordine di polinomio con 4 parametri indipendenti. Il polinomio con 4 parametri indipendenti è il polinomio di terzo grado:
$ a+b\zeta+c\zeta^{2}+d\zeta^{3} $
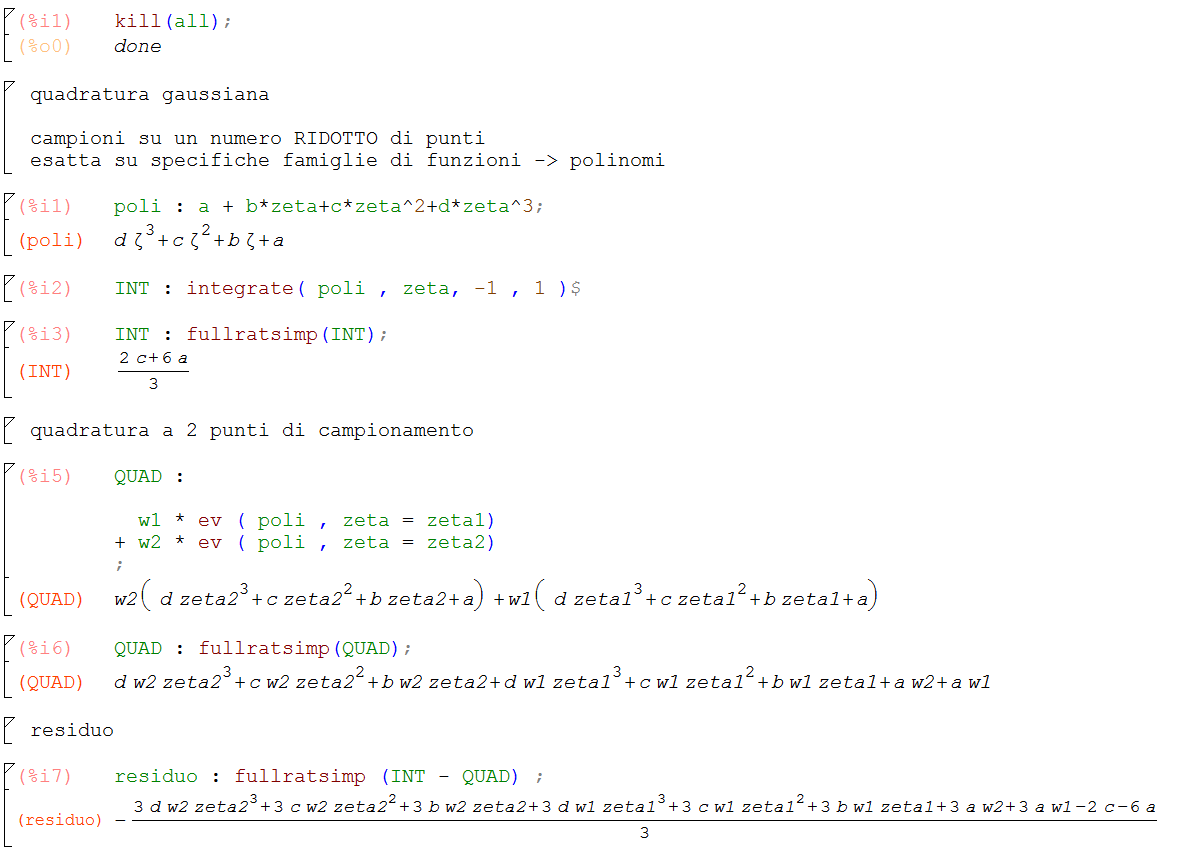
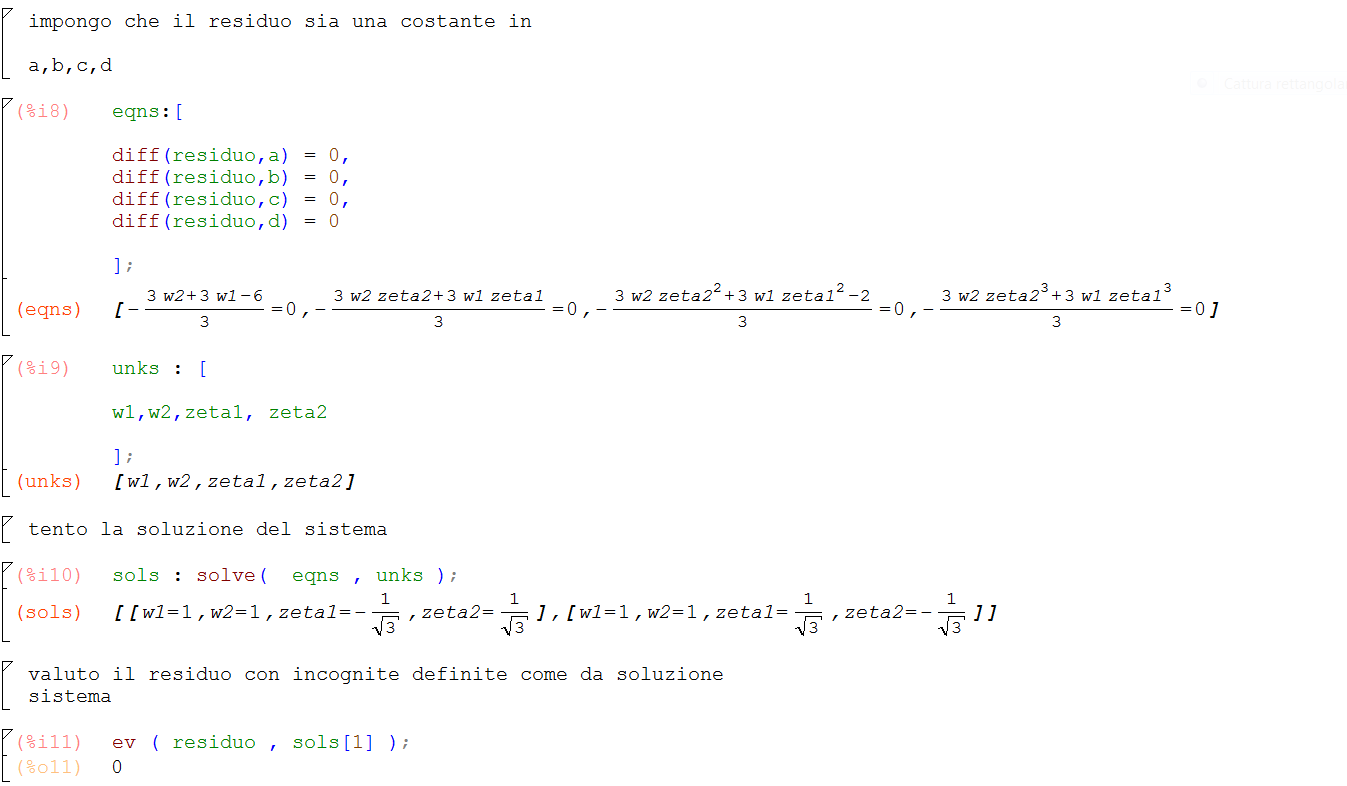
Dopo aver svolto l’integrale esatto e la quadratura gaussiana a 2 punti di campionamento, si calcola il residuo, cioè la differenza tra i risultati dei due metodi. Il residuo deve essere nullo per ogni a,b,c,d, cioè per ogni polinomio di 3° grado. Il residuo, se è nullo per ogni a,b,c,d, deve essere almeno costante per ogni valore dei parametri indipendenti, in modo da avere tutte le derivate rispetto ad a,b,c,d nulle. Quindi è stata definita una lista di 4 equazioni; questo è un sistema di equazioni non lineari,che contiene anche dei termini di ordine 4. Vengono poi definite le 4 incognite, e si va a tentare la soluzione del sistema tramite il solve. Ottengo 2 soluzioni:
$ w_{1}=1,w_{2}=1,\zeta_{1}=-\frac{1}{\sqrt{3}},\zeta_{2}=\frac{1}{\sqrt{3}} $
$ w_{1}=1,w_{2}=1,\zeta_{1}=\frac{1}{\sqrt{3}},\zeta_{2}=-\frac{1}{\sqrt{3}} $
Siccome entrambi i punti di campionamento hanno lo stesso peso, è indifferente considerare l’una o l’altra soluzione. Si va quindi a valutare il residuo nella soluzione specifica, con incognite definite come da soluzione del sistema. Si verifica che i pesi che rendono costante il residuo lo rendono anche nullo.
$\int_{-1}^{1}g(\zeta)d\zeta=1\cdot g(-\frac{1}{\sqrt{3}})+1\cdot g(\frac{1}{\sqrt{3}})$
Una quadratura gaussiana di ordine 2 integra esattamente una funzione di 3° grado.
Per N=1 si ha $ \zeta_{1}=0,w_{1}=2 $.
Una quadratura gaussiana di ordine 1 integra esattamente una funzione di 1° grado lineare.In generale, una quadratura gaussiana di ordine N integra esattamente una funzione di grado 2N-1. Se la funzione g non è un polinomio, il risultato della quadratura non è esatto ma approssimato.
Applichiamo la quadratura gaussiana al nostro caso specifico, per ricavare la matrice di rigidezza K.
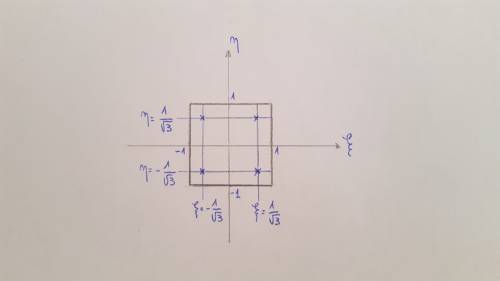
Siamo sul dominio: $\xi$ compreso tra -1 e 1, $\eta$ compreso tra -1 e 1. Comincio a svolgere l’integrale più esterno, utilizzando la regola di quadratura a 2 punti, con pesi unitari:
$K=\iint_{-1}^{1}F(\xi,\eta)d\xi d\eta\simeq 1\cdot \int_{-1}^{1}F(\xi,-\frac{1}{\sqrt{3}})d\xi+1\cdot \int_{-1}^{1}F(\xi,\frac{1}{\sqrt{3}})d\xi$
Questo tipo di campionamento prevederebbe di agire solo sui punti del dominio con coordinate $\eta=-\frac{1}{\sqrt{3}}$ e $\eta=\frac{1}{\sqrt{3}}$ (due segmenti). Anche questi integrali devono essere svolti per quadratura gaussiana:
$K\simeq1\left [ 1\cdot F(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}})+1\cdot F(\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}})+1\cdot F(-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})+1\cdot F(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}) \right ]$
In pratica l’ integrale è pari alla somma di queste 4 componenti, moltiplicate per peso unitario. Non vado quindi a campionare la funzione su tutto il segmento, ma solo in 4 punti, detti punti di Gauss dell’elemento isoparametrico 4 nodi. Quindi alla regola di quadratura a 2 punti corrispondono 4 punti di Gauss.
Apriamo una parentesi, vedendo come disegnare un elemento in coordinate $\xi$, $\eta$ sul piano fisico x,y.
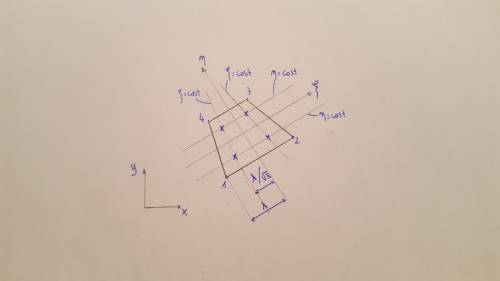
Ci si basa sul fatto che muovendosi su $\xi=cost$ e $\eta=cost$ si ha una trasformazione lineare; per cui il punto medio di un lato (luogo di punti in cui $\eta=cost$), il lato viene trasformato linearmente nel suo corrispettivo. Tutti gli elementi di centro lato dell’elemento in $\xi,\eta$ sono a centro lato anche in x,y , qualunque sia la forma dell’elemento. Se voglio trovare i punti di Gauss che avevo in $\xi,\eta$ anche in x,y ,vado a prendere i punti per i quali il rapporto di distanza è $\lambda/\sqrt{3}$ a $\lambda$. Infatti poiché il segmento viene trasformato attraverso trasformazione lineare, il rapporto $1/\sqrt{3}$ a $1$ col metà lato per identificare il punto di Gauss si mantiene anche sul segmento trasformato. A questo punto riesco a tracciare delle rette a $\xi=cost$ e $\eta=cost$.
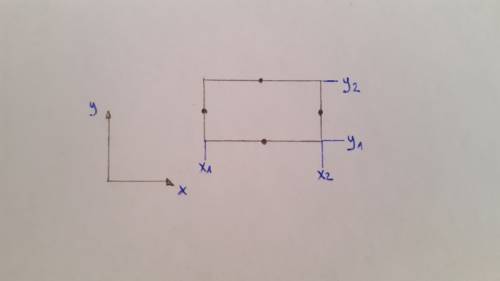
Nel nostro caso specifico, la trasformazione lineare sarà:
$ x(\xi,\eta)=\frac{x_{1}+x_{2}}{2}+\frac{x_{2}-x_{1}}{2}\xi $ Con nessuna dipendenza da $\eta$.
Abbiamo che il determinante della matrice jacobiana è costante sull’elemento se x e y sono funzioni lineari di $\xi$ e $\eta$ (cioè la trasformazione $x,y-\xi,\eta$ manca del termine quadratico), per cui tutte le derivate sono costanti.
$$ \left | J \right |=\begin{bmatrix}
\frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi}\\
\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta}
\end{bmatrix} $$
Consideriamo lo jacobiano costante: abbiamo che il suo determinante è di ordine 0, in quanto $\xi$ ed $\eta$ compaiono nel determinante con potenze di ordine 0).
$ F(\xi,\eta)=B^{T}(\xi,\eta)DB(\xi,\eta)\left | J(\xi,\eta) \right | $
$\xi$ e $\eta$ non sono nel legame costitutivo, quindi la matrice D è di ordine 0. La matrice B, così come B trasposta, ha una dipendenza di ordine $\lambda$ da $\xi$ e $\eta$, quindi la funzione è un polinomio di ordine $\lambda^{2}$ in $\xi$ ed $\eta$. Vediamo dove entra, in B, lo jacobiano:
$B(\xi,\eta)=HJ_{inv}^{*}Q$
La matrice Q è di ordine lineare in $\xi$ e $\eta$, mentre la matrice H essendo formata soltanto da 0 ed 1, sarà di ordine 0. Nel caso specifico in cui il determinante della matrice jacobiana è costante, anche la matrice $J_{inv}^{*}$ è di ordine 0, quindi si avrà che $\lambda=1$. Di conseguenza tutto l’integrando è una funzione di ordine 2 in $\xi$ e $\eta$.
Quindi nel caso particolarissimo di elementi in cui la matrice jacobiana sia costante, per l’elemento isoparametrico a 4 nodi con la quadratura a N=2 ho una valutazione esatta della matrice di rigidezza, nell’ ipotesi ulteriore che D sia costante. Con una quadratura gaussiana a un solo punto sull’intervallo lineare ( N=1), avrei campionato l’integrale in $\xi=0$ e $\eta=0$, cioè nel centroide. Con N=1, posso calcolare in forma esatta l’integrale di funzioni lineari; ma dato che nel nostro caso l’integrando è in forma quadratica, ottengo un’ integrazione approssimata di K. La quadratura con N=2 è la minima quadratura gaussiana che dà una matrice di rigidezza esatta per l’elemento. Un campionamento a più di 2 punti di Gauss sull’intervallo avrebbe senso solo nell’ottica di lavorare con elementi distorti.
Di solito i codici a elementi finiti implementano gli elementi in 2 forme:
- Elementi implementati con la minima regola di integrazione gaussiana che dà la matrice di rigidezza esatta su elementi non distorti, cioè a Jacobiano costante (elementi full intregration).
- Implementano una variante dell’ elemento a integrazione approssimata (elementi reduced integration).
Quindi nel caso dell’ isoparametrico 4 nodi, saranno implementate le quadrature a N=2 come full integration, e a N=1 come reduced integration.
Vediamo un problema degli elementi sottointegrati, in particolare per quadratura a N=1. Essendo lo stato deformativo campionato solo al centroide, tutti i moti dell’ elemento che non deformano il centroide sono moti in cui $\epsilon=0$ . Se campiono $\sigma$ ed $\epsilon$ solo al centroide, tutti i moti che non deformano il centroide sono moti in cui l’ integrando è nullo, quindi sono moti a cui non è associata energia potenziale elastica.
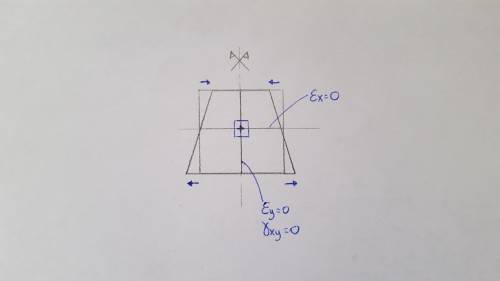
Vediamo ad esempio una deformazione trapezia dell’ isoparametrico 4 nodi. Questa deformazione definisce un campo degli spostamenti, che derivando in x e y dà il campo delle deformazioni. Ho un segmento orizzontale in cui $\epsilon_{x}=0$. Ho un segmento verticale in cui $\epsilon_{y}=0$; inoltre ho che la deformazione è simmetrica rispetto ad un asse, per cui la componente antisimmetrica $\gamma_{xy}=0$. Quindi il centroide, con questo tipo di deformazione dell’elemento, è del tutto in deformato. Quindi dato che questo quadratino è rappresentativo di tutto l’elemento, a quel moto deformativo dell’ elemento non è associata in nessun punto dell’elemento campionato una deformazione (quindi nemmeno una tensione se la legge è lineare). Di conseguenza non avrà energia potenziale elastica associata. Questo moto sarà del tutto equivalente energeticamente ad un moto di corpo rigido.
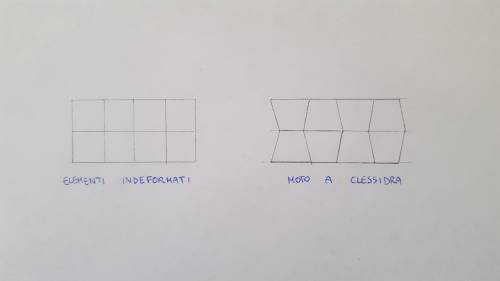
Se una mesh con questo tipo di elementi è costante, ogni elemento si trasforma trapezoidalmente con continuità insieme agli altri. Questo moto (detto moto a clessidra) è equivalente energeticamente ad un moto di corpo rigido,se l’ elemento è a tecnologia sottointegrata. Se campionassi la matrice di rigidezza a N=2, i 4 punti, sotto quel campo di spostamenti, si deformano.
Gli elementi sottointegrati sono utili per vari motivi: avendo un solo punto di campionamento, il costo computazionale è inferiore rispetto ad una quadratura a N maggiore. Inoltre, sempre per il fatto di avere 1 solo punto di campionamento, avremo che l’elemento o è tutto elastico o tutto snervato (non si avrà mai un legame costitutivo elstico-lineare, più complicato).
Abbiamo quindi definito la procedura per il calcolo della matrice di rigidezza per un elemento isoparametrico 4 nodi. Se lo Jacobiano non fosse uniforme, abbiamo che (nel caso ad esempio di una matrice quadrata):
$$ J^{-1}=\frac{1}{ad-bc}\begin{bmatrix}
d & -b \\
c & a
\end{bmatrix} $$
$(ad-bc)$ è un termine di ordine 2 in $\xi$ e $\eta$ (perché a, b, c, d possono essere lineari in $\xi$ e $\eta$). $J^{-1}$ è una funzione razionale fratta, mi aspetto che il denominatore arrivi ad avere una frazione di ordine 4 nella complessità del sistema, il che lo rende difficilmente gestibile con integrazione esatta.
RIDUZIONE DEI CARICHI DISTRIBUITI A CARICHI CONCENTRATI NODALI
Possiamo considerare un elemento triangolare a tre nodi i, j, k, o equivalentemente un elemento a quattro nodi i, j, k, l.
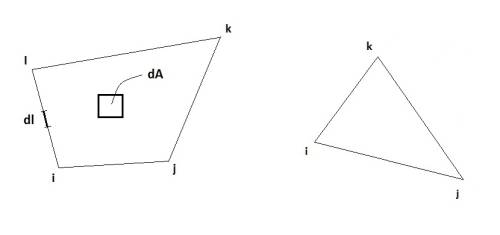 Di solito viene fatta un'analisi energetica per la riduzione di carichi di volume o di superficie. Supponiamo di avere dei carichi per unità di volume (nelle nostre trattazioni ci siamo sempre riferiti ad elementi piani, ma ricordiamoci che avranno anche uno spessore tale che il volume è $dV=t \: dA$), di componenti qx e qy [N/mm^3] rispettivamente in direzione x e y; tali possono essere dovuti al peso proprio, a forze inerziali, centrifughe ecc… Possiamo avere inoltre dei carichi distibuiti sulla superficie dell'elemento (negli elementi presi in considerazione $dA=dl \: t$ dove dl è il tratto infinitesimo che collega due nodi), che posso scomporre in componenti Sx e Sy [N/mm^2]; tale scomposizione può essere fatta anzichè sugli assi di riferimento globali, sulla direzione normale e tangenziale della linea dell'elemento locale (in 2D ho solo una direzione tangenziale, in 3D ne ho due).
Di solito viene fatta un'analisi energetica per la riduzione di carichi di volume o di superficie. Supponiamo di avere dei carichi per unità di volume (nelle nostre trattazioni ci siamo sempre riferiti ad elementi piani, ma ricordiamoci che avranno anche uno spessore tale che il volume è $dV=t \: dA$), di componenti qx e qy [N/mm^3] rispettivamente in direzione x e y; tali possono essere dovuti al peso proprio, a forze inerziali, centrifughe ecc… Possiamo avere inoltre dei carichi distibuiti sulla superficie dell'elemento (negli elementi presi in considerazione $dA=dl \: t$ dove dl è il tratto infinitesimo che collega due nodi), che posso scomporre in componenti Sx e Sy [N/mm^2]; tale scomposizione può essere fatta anzichè sugli assi di riferimento globali, sulla direzione normale e tangenziale della linea dell'elemento locale (in 2D ho solo una direzione tangenziale, in 3D ne ho due).
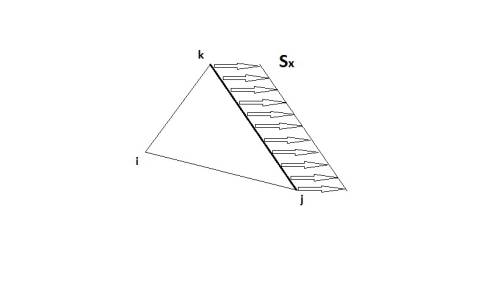 Supponiamo che siano applicate Sx, Sy, qx e qy che possono essere costanti oppure una funzione di x e y (esempio della pressione idrostatica agente sulla diga che aumenta linearmente con la profondità, oppure la farfalla tensionale di un elemento soggetto a momento flettente che varia linearmente lungo la sezione). Le equazioni di equilibrio sono sempre riferite a forze concentrate; dunque, come ridurre sui tre o quattro nodi le forze distribuite con forze nodali equivalenti F? Questo vettore F ha una componente per ogni g.d.l. dell'elemento, quindi in realtà più che forze nodali sono forze base-grado di libertà. Mi aspetto che i carichi distribuiti lungo x diano una componente delle forze nodali lungo x, e lo stesso per y.
Supponiamo che siano applicate Sx, Sy, qx e qy che possono essere costanti oppure una funzione di x e y (esempio della pressione idrostatica agente sulla diga che aumenta linearmente con la profondità, oppure la farfalla tensionale di un elemento soggetto a momento flettente che varia linearmente lungo la sezione). Le equazioni di equilibrio sono sempre riferite a forze concentrate; dunque, come ridurre sui tre o quattro nodi le forze distribuite con forze nodali equivalenti F? Questo vettore F ha una componente per ogni g.d.l. dell'elemento, quindi in realtà più che forze nodali sono forze base-grado di libertà. Mi aspetto che i carichi distribuiti lungo x diano una componente delle forze nodali lungo x, e lo stesso per y.
Si potrebbe tentare di definire i carichi nodali equivalenti sulla base di condizioni di equilibrio alle forze e ai momenti; tuttavia il numero di equazioni può non coincidere con il numero di azioni incognite sui g.d.l. nodali, o in alternativa tali equazioni possono risultare non indipendenti. Tento allora un approccio diverso.
Definisco quindi tale 'Equivalenza' su base energetica, ossia preso un qualsiasi moto (rototraslatorio o deformativo) dell'elemento compatibile con le funzioni di forma (ad esempio in un iso4 i lati devono rimanere rettilinei), il lavoro svolto su questo moto dalle forze distribuite deve essere pari a quello delle forze concentrate equivalenti nodali.
Risulterà che quel sistema di forze distribuite e concentrate avranno pari risultante e pari momento risultante? Certamente sì, perchè la risultante delle forze in x compie lavoro in direzione x, lo stesso per y, e per i momenti sulle rotazioni, pertanto dalle considerazioni di equivalenza energetica le risultanti devono essere le stesse perchè altrimenti il lavoro differirebbe.
Introduciamo il concetto di 'qualunque possibile deformazione'. Tali deformazioni devono soddisfare certi vincoli, per esempio $U (\xi,\eta )$ e $V (\xi,\eta)$ devono rispettare i vincoli determinati dalla cinematica interna dell'elemento, cioè tali spostamenti devono essere ricavabili dalle funzioni di forma dell'elemento. Per esempio sarà per un elemento quadrilatero 4 nodi: $$\begin{bmatrix}
U (\xi,\eta)\\
V (\xi,\eta)
\end{bmatrix}=
\begin{bmatrix}
N_i & 0 & N_j & 0 & N_k & 0 & N_l & 0\\
0 & N_i & 0 & N_j & 0 & N_k & 0 & N_l
\end{bmatrix}
\begin{bmatrix}
u_i\\
v_i\\
u_j\\
v_j\\
u_k\\
v_k\\
u_l\\
v_l
\end{bmatrix}$$. Definisco il vettore colonna degli spostamenti nodali come d (otto elementi per 4 nodi, sei per i 3 nodi), e contiene i gradi di libertà dei nodi. La matrice centrale invece la definisco N, dove le N sono le funzioni di forma, funzioni di ξ ed η.
Pertanto la relazione scritta sopra è: $$\underline{U}=\underline{\underline{N}} (\xi,\eta) \underline{d}$$
Funzioni di forma per elementi triangolari a tre nodi
Esse sono funzioni lineari sull'elemento, valgono 1 sui nodi cui sono associati, e 0 sugli altri. Definizione sostanzialmente geometrica: se prendo un punto di coordinate (x,y), e costruisco tre aree unendo tale punto con i nodi (regola di interpolazione su domini triangolari), definisco Ai l'area che non tocca il nodo i (cioè è opposta ad esso); Ai è una funzione di x e y, e le altre due aree vengono chiamate aj e ak anch'esse funzioni di x e y.
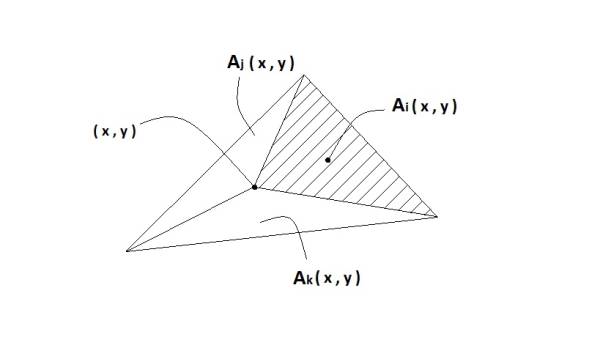 La funzione di forma di forma associata al nodo i è definita come:
La funzione di forma di forma associata al nodo i è definita come:
$N_i=(A_i)/a_{tot}$
E così definisco anche le altre due funzioni di forma:
$N_j=(A_j)/a_{tot}$
$N_i=(A_k)/a_{tot}$
Se il punto si avvicina al nodo i, allora l'area Ai tende ad 1, se si allontana andando verso uno qualsiasi degli altri due nodi va a 0.
A questo punto utilizzo la regola del determinante per la determinazione dell'area Ai:
$$A_i = \begin{vmatrix}
1 & 1 & 1 \\
x & x_j & x_k \\
y & y_j & y_k
\end{vmatrix} \frac{1}{2!}
$$
Ottengo termini lineari in x e y in quanto non sono presenti contemporaneamente in nessun addendo del determinante, e si può affermare pertanto che l'area è lineare rispetto ad x e y. Con tali determinanti abbiamo trovato le funzioni di forma per l'elemento triangolare. Dunque lo spostamento U di un generico punto all'interno dell'elemento sarà dato dall'interpolazione lineare:
$$U(x,y)=u_iN_i(x,y)+u_jN_j(x,y)+u_kN_k(x,y)$$
Determinazione delle forze concentrate equivalenti
Le funzioni di forma servono per descrivere una famiglia di spostamenti che le rispettano, che sono quelli ottenibili dal prodotto $\underline{U}=\underline{\underline{N}} (\xi,\eta) \underline{d}$.
L'equivalenza energetica non deve valere per un generico spostamento, ma solo quelli che sono esprimibili per mezzo della formula sopra.
Si passa al calcolo del lavoro fatto dalle forze di volume qx e qy per unità di volume:
$$\begin{bmatrix}
q_x\\
q_y
\end{bmatrix}^T
\underline{U}(\xi,\eta)dV\; \rightarrow\;
(q_xu(\xi,\eta)+q_yv(\xi,\eta))dV
$$
Adesso integro sull'intero volume:
$$
W_q = \int \int \int_V \begin{bmatrix}
q_x\\
q_y
\end{bmatrix}^T
\underline{U}(\xi,\eta)dV
=
\int \int \int_V \begin{bmatrix}
q_x & q_y
\end{bmatrix}\underline{\underline{N}}( \xi ,\eta)\underline{d}dV
$$
Il vettore degli spostamenti nodali è una costante nell'integrale (non variano al variare del punto considerato all'interno dell'elemento).
Per cui:
$$
W_q =( \int \int \int_V \begin{bmatrix}
q_x & q_y
\end{bmatrix}\underline{\underline{N}}( \xi ,\eta)dV)\underline{d}
$$
Analogamente per le forze S, integrando sulla superficie dell'elemento otteniamo:
$$
W_s=(\int \int _S\begin{bmatrix}
S_x & S_y
\end{bmatrix}\underline{\underline{N}}( \xi ,\eta)dS)\underline{d}
$$
In realtà si potrebbe pensare come integrale di linea piuttosto che come integrale di superficie per elementi bidimensionali, moltiplicandolo per lo spessore t costante.
Il lavoro delle forze concentrate equivalenti sugli stessi spostamenti d è semplicemente il vettore:
$$
W_F=\underline{F}^T\underline{d}=[F_{xi},F_{yi},F_{xj},F_{yj},F_{xk},F_{yk},F_{xl},F_{yl}]\underline{d}
$$
Eguagliando, noto che ambo i membri moltiplicano il vettore d, per cui avrò:
$$
\underline{F}^T=
\int \int _S\begin{bmatrix}
S_x & S_y
\end{bmatrix}\underline{\underline{N}}( \xi ,\eta)dS +
\int \int \int_V \begin{bmatrix}
q_x & q_y
\end{bmatrix}\underline{\underline{N}}( \xi ,\eta)dV
$$
$$
W_F=W_q+W_s\; \; \; \forall d
$$
Dunque il passaggio da forze distribuite a forze nodali si ha per le funzioni di forma associate ad ogni nodo.
Autori
Fabio Mortellaro , Carlo Laurino ,

Discussione
REVISORE 1
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
No.
Il testo proposto è coerente con gli appunti personali del revisore?
Sì.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Non strettamente necessario.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Nel suo complesso la procedura di quadratura gaussiana risulta esposta in modo inorganico.
Sarebbe molto difficile capire il metodo senza attingere ad altri testi.
Riporto, nel pdf allegato, una sintesi del metodo esposta, in mia opinione, in modo più fluido.
Tralascerò passaggi matematici già spiegati, considerazioni sul caso di ordine di quadratura pari ad 1 e altri dettagli già spiegati.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
Se anche la revisione inviata dovesse essere insufficiente, sì. Per quanto la descrizione della Quadratura di Gauss sia sovrabbondante in testi e rete, non sono facilmente fruibili informazioni sul particolare metodo di determinazione delle incognite(punti di campionamento e pesi) usato in classe.
Ore dedicate a questa revisione
3 ore.