Indice
Caratterizzazione simmetrica e antisimmetrica dei modi propri di strutture simmetriche
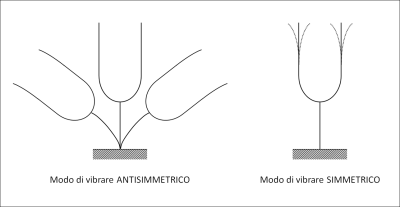
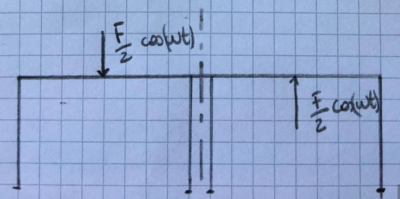
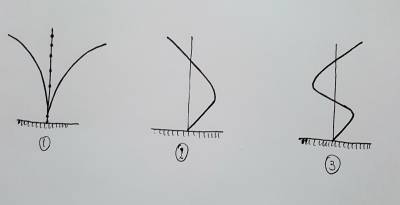
Per una struttura in cui esiste una simmetria geometrica, di massa, di materiale (modulo di Young E) e di vincolamento, i modi propri di vibrare possono essere esclusivamente simmetrici e antisimmetrici. Considerando l’esempio di una struttura simmetrica a forma di diapason è possibile estrapolare facilmente (come in figura 1) due modi di vibrare: uno simmetrico e uno antisimmetrico.
In una struttura ci saranno tanti modi propri quanti sono i gradi di libertà per ogni nodo. Ma non tutti questi modi sono di particolare interesse per l’analisi dinamica: potremo non considerare quei modi che hanno frequenza molto maggiore a quella di risonanza. Dobbiamo tener in considerazione, infatti, tutti quei modi che hanno frequenza all’interno del range nel quale lavora la forzante, perché solo questi posso essere mandati in risonanza. Dopo una certa frequenza l’eccitante è debole abbastanza, rispetto lo smorzamento del corpo (anche se minimo), e quindi non potranno più insorgere dei problemi
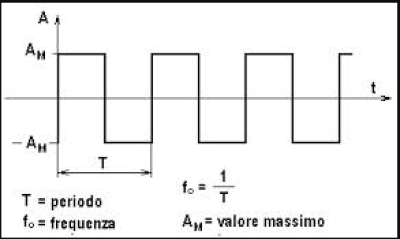
Se il sistema è eccitato da un’onda quadra (figura 2), ovvero un segnale che oscilla da un valore massimo ad uno minimo, come ad esempio un interruttore di corrente On/Off, facendo lo sviluppo in serie di Fourier, si ottiene uno sviluppo non finito, con n tendente ad infinito. Di conseguenza si ha che: $$A(t)=\sum_{i=1}^{n}(_{bi}\cdot \cos (i2\pi \frac{1}{T}t))$$ Dove A(t) è l’ampiezza del segnale nel tempo, T è il periodo, 1/T è la frequenza e $2\pi \frac{1}{T}=\omega $ è la pulsazione. Dopo una certa frequenza (tronchiamo quindi lo sviluppo per renderlo finito), le eccitanti con una frequenza superiore non mi interessano più (componenti del segnale trascurabili perché deboli) poiché il corpo ha quel minimo di smorzamento che fa si che l’ampiezza in risonanza sia limitata (Risonanza= fenomeno per cui l'ampiezza delle oscillazioni indotte in un sistema oscillante, meccanico o elettrico, sollecitato da una forza esterna, assume in determinate condizioni valori molto elevati). Però, in assenza di smorzamento ogni eccitante può essere problematica. Le eccitazioni ad alta frequenza possono essere dannose non solo per motivi strutturali, ma anche per motivi ergonomici: secondo le normative, nei posti di lavoro occorre ridurre il rumore percepito dall'udito umano e per tale motivo bisogna evitare risonanze nel range dell’udito.
Inoltre, non vanno considerati quei modi propri al di sotto di una soglia minima di frequenza, perché al di sotto di quel valore non avremo un'eccitante. I motori asincroni, ad esempio, non funzionano sotto una certa soglia (50 Hz).
Di solito quindi, viene considerato un sottoinsieme dei modi propri, perché o sotto una certa soglia di frequenza non c’è un’eccitante o perché, sopra una certa soglia di frequenza l’eccitante è debole e quindi non interessante dal punto di vista ingegneristico.
Analisi nodale di una struttura eccitata da una forzante di pulsazione propria con smorzamento
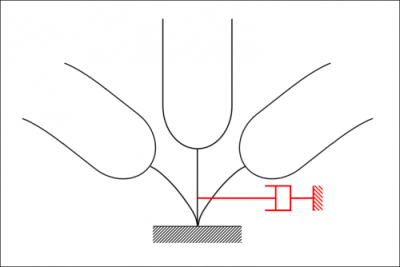
Supponiamo adesso che sul diapason (struttura simmetrica) vi sia collegato uno smorzatore come in figura 3.
Per l’analisi nodale di una struttura eccitata da una forzante, il sistema di equazioni differenziali del moto è: $$M\ddot{\bar{x}}+C\dot{\bar{x}}+K\bar{x}=\bar{F}(t)$$ Se la forzante è del tipo $\bar{F}(t)=\bar{f}\cdot e^{jw_{i}t}$ con $w_{i}$ pari ad una pulsazione propria del moto libero del sistema non smorzato, allora il sistema avrà soluzione del tipo $\bar{x}(t)=Q_{i}\bar{x_{i}}e^{jw_{i}t}$. Calcolando le derivate della soluzione per ottenere la velocità e l’accelerazione, e sostituendo all’equazione iniziale (1), otteniamo: $$\alpha_{i}(K-\omega _{i}^{2})\bar{x_{i}}+a_{i}j\omega _{i}C\bar{x_{i}}=\bar{f}$$ e poiché $w_{i}$ è una pulsazione propria del sistema non smorzato si ha che: $$(K-\omega_{i}M)=\bar{0}$$ E di conseguenza $a_{i}j\omega _{i}C\bar{x_{i}}$. Ciò significa che le forze esterne posso essere bilanciate solo dal contributo dello smorzamento. E’ possibile ricavare il coefficiente $\alpha_{i}$, come: $$a_{i}=(\frac{1}{j\omega_{i}})\cdot (\frac{\bar{x_{i}^{T}\bar{f}}}{\bar{x_{i}^{T}}C\bar{x_{i}}})$$ In cui C è la matrice smorzamento, ed ha la forma: $$\begin{pmatrix} 0 & \vdots & 0\\ ... & c & ...\\ 0 & \vdots & 0 \end{pmatrix}$$
C ha tutti gli elementi nulli tranne nell’elemento smorzante, in corrispondenza della riga e della colonna associate allo spostamento lungo x del nodo della struttura in cui è collegato lo smorzatore. Tutti gli smorzamenti collegati a terra, e non con un altro punto della stessa struttura, sono disposti sulla diagonale di tale matrice, poiché non ci saranno dei moti relativi tra gli elementi che compongono il diapason.
Se ad esempio, il nodo collegato allo smorzatore è il 123, allora l’elemento smorzante si troverà sulla colonna e sulla riga: 122*6+1=733. (122=numero di nodi prima dello stoccaggio; 6=gradi di libertà)
Il denominatore dell’equazione (2) può essere considerato come: $$\bar{x_{i}^{T}}C\bar{x}_{i}=c[\bar{x_{i}}]_{733}^{2}=cu_{123}^{2}$$ Dove u è lo spostamento in x del nodo considerato.
Il numeratore della (2), dal punto di vista fisico corrisponde all’accoppiamento tra la forzante e il modo proprio, infatti per esempio, un modo proprio simmetrico può essere eccitato solo da una forzante simmetrica, e analogamente un modo antisimmetrico solo da una forzante antisimmetrica.
Scomposizione di una forza in una componente simmetrica e in una antisimmetrica
I modi simmetrici o antisimmetrici possono essere eccitati, ovvero possono avere numeratore non nullo solo se la forzante è rispettivamente simmetrica e antisimmetrica (si ricordi che, come già detto, un modo simmetrico non può essere eccitato da una forzante antisimmetrica e viceversa). Poiché le forzanti possono essere né simmetriche né antisimmetriche possono essere scomposte in una componente simmetrica e in una antisimmetrica.
Consideriamo un sistema con geometria simmetrica (per esempio un tavolo) ma sollecitato da un carico (una forzante) che non sia né simmetrico né antisimmetrico rispetto al piano di simmetria della struttura, come in figura 4.
Vogliamo adesso estrarre la parte simmetrica e la parte antisimmetrica della sollecitazione. Di conseguenza, supponendo che il sistema sia lineare e che quindi può essere applicato il principio di sovrapposizione degli effetti, potremo considerare questo sistema come l’unione di due parti: una simmetrica e una antisimmetrica. Si ha quindi che:
In figura 5 è rappresentata la parte simmetrica in cui il carico è simmetrico e quindi viene equamente diviso sulle due parti del sistema. Nella figura 6 vi è la parte antisimmetrica, ottenuta sottraendo alla struttura originale la parte simmetrica.
Potremo quindi scomporre un problema, in due più semplici per poi sommare i risultati ottenuti attraverso il principio di sovrapposizione degli effetti.
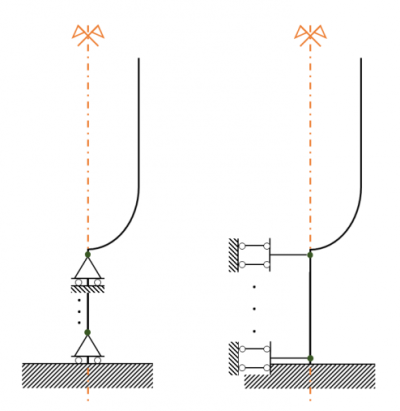
Si deve ricordare però, che alla parte simmetrica del problema vanno imposti nulli lo spostamento ortogonale al piano di simmetria (Ux=0) e le rotazioni con asse paralleli agli assi del piano (θy=0; θz=0, rotazioni entro piano), per garantire la continuità del materiale. Per tale motivo vincoleremo tale parte attraverso un doppio pendolo. Inoltre, ciò che è libero nella simmetria deve essere bloccato nell’antisimmetria, pertanto in questo caso utilizzeremo per il vincolamento un carrello (Uy=0; Uz=0; θx=0), come mostrato in figura 7.
Approfondimento simmetrie e antisimmetrie
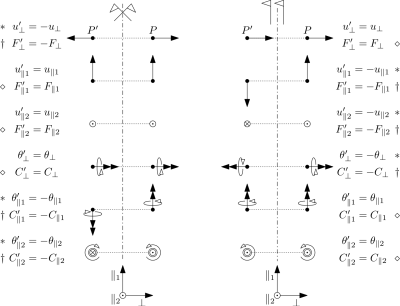
Si consideri la seguente immagine:
Nella parte di sinistra vengono rappresentati una serie di casi simmetrici, mentre nella parte di destra di casi antisimmetrici. Analizziamo i casi simmetrici.
Le prime 2 immagini mostrano le direzioni e i versi che due forze dovrebbero avere per essere definite simmetriche, analogamente per le immagini seguenti, che mostrano casi di coppie simmetriche. Di conseguenza è importante definire quando 2 forze/coppie risultano simmetriche:
- Due forze con direzione normale al piano di simmetria sono simmetriche se non sono equiverse
- Due forze parallele allo stesso piano di simmetria sono simmetriche se equiverse
- Due coppie ad asse perpendicolare al piano di simmetria sono simmetriche se equiverse
- Due coppie ad asse parallelo al piano di simmetria sono simmetriche se opposte in verso (quindi una coppia sarà uscente e una entrante)
Lo stesso tipo di informazioni può essere dedotto per le forze/coppie antisimmetriche leggendo la parte destra dell’immagine.
Osservazione: ⋄ e ∗ si riferiscono rispettivamente a componenti di spostamento e a componenti di azione interna nulle al piano di simmetria/antisimmetria, in particolare:
- ∗ l’asterisco indica che gli spostamenti riportati accanto a questo simbolo devono essere nulli per garantire la continuità del materiale
- ⋄ indica che gli spostamenti devono essere nulli per non violare il principio di azione/reazione
Esempio
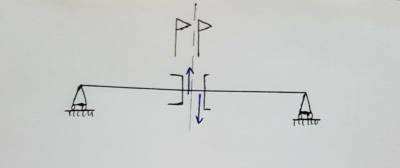
I nodi all’intersezione tra la struttura elastica e il piano di antisimmetria vengono vincolati come segue. Si consideri una trave in un caso antisimmetrico. Se il sistema è antisimmetrico e il nodo P si muove verso l’alto (quindi entro piano, perché il piano è formato dalle due direzioni, una uscente e una che punta verso l’alto), l’antisimmetria prescrive che il nodo opposto si deve spostare verso il basso, come è indicato nell’immagine.
Imponendo questa condizione, si genera però uno scorrimento tra le due sezioni del materiale, per cui al fine di garantire la continuità dello stesso, bisogna impedire gli spostamenti entro piano. Infatti se la continuità del materiale impone che i 2 punti si muovano nello stesso verso, e se l’antisimmetria impone invece che i due punti si debbano muovere in senso opposto, l’unica soluzione possibile è quella di imporre questo spostamento entro piano nullo, per non violare né l’uno né l’altro. Di conseguenza, in generale, due spostamenti entro piano, nei punti in cui la struttura interseca il piano (in questo caso di antisimmetria) devono essere imposti nulli.
Anche la rotazione con asse normale al piano di simmetria viola la continuità del materiale, che per il caso di antisimmetria è uguale e contraria nelle due parti della struttura. Di conseguenza anche questa deve essere nulla.
Osservazione: non esiste il concetto di antisimmetria per la struttura, poiché avremo a che fare con geometrie sempre simmetriche. Tale concetto vale solo per i carichi.
Forma di Rayleigh (o forma proporzionale) per la matrice di smorzamento
I vettori associati ai modi propri, ovvero gli autovettori, diagonalizzano la matrice K e M ma non la matrice C, perché, una volta ricavati questi autovettori, C non c’è. Quindi utilizzando una base costruita con i modi propri, riusciamo a trasformare solo M e K in forma diagonale e non C. Al fine di ovviare a questo problema e di fare successivamente un’analisi di risposta semplificata per sovrapposizione modale, siamo costretti a imporre che anche C sia un oggetto diagonalizzabile se viene pre e post moltiplicato per delle matrici le cui colonne o righe sono degli autovettori. Di conseguenza invece che considerare C come una matrice generica, simmetrica di n per n elementi, la definiamo come combinazione lineare di M (matrice di massa) e di K (matrice di rigidezza), ottenendo la seguente espressione: $$C=\alpha M+\beta K$$ Ne consegue che se riusciamo a trovare una base per cui si diagonalizzano sia M sia K, allora anche C, che è combinazione lineare delle due, sarà diagonalizzata.
Osservazione: condizione sufficiente (ma non necessaria), affinché C sia diagonalizzabile, è che C sia rappresentabile in forma di Rayleigh. Se riuscissimo a rappresentare la matrice di smorzamento in questa forma con opportuni α e β, allora possiamo andare avanti e semplificare il calcolo di risposta in frequenza. Così facendo però, limitiamo i gradi di libertà della matrice C, poiché nella sua forma generica, essendo composta da n per n elementi ed essendo simmetrica, possedeva $\frac{n^{2}}{2}$ elementi indipendenti, ovvero $\frac{n^{2}}{2}$ gradi di libertà. Rappresentandola invece come combinazione lineare di M e K limitiamo i suoi gradi di libertà a 2. Passando da $\frac{n^{2}}{2}$ scalari a 2, una qualche informazione la dobbiamo perdere. Analizziamo le informazioni che perdiamo.
Riprendiamo il diapason e consideriamo un sistema di smorzatori concentrati in questa struttura.
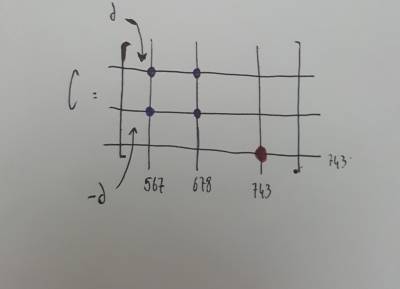
Lo spostamento x del nodo 1 è il degree of freedom 733, lo spostamento x del nodo 2 è il dof 567 mentre lo spostamento x del nodo 3 è il degree of freedom 678. Ora, la matrice smorzamento sarà uguale a una matrice composta dai seguenti termini non nulli:
- Termine diagonale di colonna e riga 733 (in rosso)
- Intersecando tra loro le colonne 567, 678 e le righe 567, 678, si ottengono 4 termini che anch’essi sono non nulli (evidenziati in figura in blu). Nei termini diagonali c’è d, mentre nei termini extra-diagonali compare -d
La matrice C si presenta quindi nella seguente forma:
Tutti gli altri elementi, esclusi questi 5 di cui sopra, sono tutti nulli.
Questa matrice presenta dunque solo 5 elementi non nulli e quindi rappresentarla come combinazione lineare di M e K, i cui termini non nulli sono molti di più di 5 (basti pensare che, almeno tutta la diagonale delle due matrici è non nulla e inoltre hanno elementi nulli sparsi) è molto complicato. Di conseguenza, pur tentando qualsiasi combinazione lineare, non riusciremmo mai a trovare una combinazione che dia come risultato la matrice C di questo caso.
Osservazione 1: quando nella struttura abbiamo degli elementi smorzanti ben definiti e progettati, cioè con caratteristica di rigidezza e di smorzamento ben tarata, (tipo l’ammortizzatore in una sospensione) allora diventa molto difficile rappresentare in forma proporzionale la matrice C perché sono presenti grossi smorzamenti locali e negli altri punti no (quindi la matrice è quasi totalmente nulla). Quindi non sempre è possibile avere una buona rappresentazione della matrice di smorzamento come somma di due fattori αM+βK.Se viceversa abbiamo che lo smorzamento della struttura è legato allo smorzamento strutturale, allora tipicamente dove c’è rigidezza, c’è smorzamento, e quindi la matrice di smorzamento diventa molto simile alla matrice K moltiplicata per un fattore. Perciò se lo smorzamento è un oggetto di tipo strutturale, allora in effetti la matrice C è rappresentabile come un βK. Questo caso è raro.
Osservazione 2: dire che C è uguale ad αM, vuol dire che c’è smorzamento in corrispondenza dei moti di corpo rigido. La matrice M non è mai singolare, quindi se consideriamo M per un moto di corpo rigido, il suo contributo non è nullo, mentre quello di K, per lo stesso moto rigido, lo è. Usando degli α non nulli, vuol dire che il sistema dissipa energia solo in traslazione, il che è strano.
Osservazione 3: questa modellizzazione funziona male anche per un sistema multi-materiale. Infatti, un sistema mono-materiale senza giunzioni (per esempio un albero motore), ha un suo smorzamento strutturale che è abbastanza preso da un βK. Ovvero l’errore di costringerci a vedere C come una combinazione lineare è basso perché si assume che α=0 e β sia una qualche numero (per mille, perché è misurato così). Mentre lo stesso discorso non vale per una struttura multi-materiale.
Per tutte le osservazioni fatte finora, sebbene questa rappresentazione di C presenti dei limiti, viene comunque ampiamente accettata perché la capacità di rappresentare lo smorzamento delle strutture è ancora più limitata (infatti nessuno si mette a misurare gli $\frac{n^{2}}{2}$ termini della matrice C nella sua forma generica).
L’entità delle informazioni sullo smorzamento quando approcciamo al calcolo della struttura è molto limitata quindi per questo motivo ci si appoggia sempre a delle normative, dalle quali si possono ricavare i valori di αM+βK.
Se è possibile calcolare C come combinazione lineare di M e K (sempre smorzamenti strutturali) allora possiamo andare avanti e procedere con un’analisi di risposta semplificata.
Analisi di risposta per sovrapposizione modale
Come appena detto, calcolata C, procediamo con l’analisi. Nel caso gli autovalori associati ai modi propri siano tutti distinti (se non lo sono perturbiamo la struttura affinché lo siano, basta spostare un nodo della mesh), vigono le condizioni di ortogonalità, ovvero un autovettore trasposto per la matrice massa per un altro autovettore, dà 1 se si sta parlando dello stesso vettore e 0 se sono due autovettori distinti: $$\hat{x_{j}^{T}}M\hat{x_{i}}=\delta _{ji}$$ Viceversa per la matrice di rigidezza, il prodotto K per xi è uguale a wi se i=j, altrimenti è uguale a 0 se i è diverso da j: $$\hat{x_{j}^{T}}K\hat{x_{i}}=\delta _{ji}\omega _{i}^{2}$$ con $\delta _{ji}$ delta di Kroneker (è uguale a 1 se i=j altrimenti è uguale a 0) Se gli autovettori non fossero normalizzati si otterrebbe la massa modale (che risulta unitaria se gli autovettori fossero normalizzati a massa unitaria). Quindi per sapere quanto vale la massa modale associata a un modo proprio, bisogna prendere l’autovettore e moltiplicarlo per il suo trasposto e per la massa, ottenendo: $$\hat{x_{i}^{T}}M\hat{x_{i}}=m_{i}$$ A questo punto consideriamo i primi m autovettori (consideriamo quindi solo un sottoinsieme dei modi propri). Facendo ciò, semplifichiamo il problema e vietiamo al sistema di muoversi nelle forme previste dagli autovettori che abbiamo trascurato. Implicitamente stiamo dicendo che non solo il sistema deve muoversi secondo le funzioni di forma previste da ogni specifico elemento (concetto base de FEM), ma anche che non sono possibili tutti i moti, ma solo quelli ottenibili come combinazione lineare di quelli concessi.
Ciò vuol dire che se prendiamo una trave puramente flessionale (ogni nodo può solo muoversi o ruotare quindi ha 2 gdl), incastrata nel piano, discretizzata con 6 nodi e consideriamo i seguenti modi propri (quelli appartenenti a m, m=3 in questo caso):
la struttura ha 12 gdl e quindi può avere ∞^12 soluzioni rappresentabili per sola discretizzazione FEM, ognuno dei nodi può muoversi indipendentemente dagli altri. Imponendo però m=3, diciamo che la struttura da ∞^12 possibili configurazioni (modi di vibrare), ce ne ha solo ∞^3, dovute alle combinazioni lineari dei modi rappresentati nella figura precedente. Troncando quindi la struttura al terzo modo proprio, è come se la stessa fosse infinitamente rigida al quarto.
In questo modo si ottiene una semplificazione cinematica ulteriore rispetto al FEM. Per quanto detto è quindi importante capire come definire la soglia alla quale si smettono di considerare i modi propri, perché da lì in poi è come se il sistema non potesse più muoversi e quindi deformarsi.