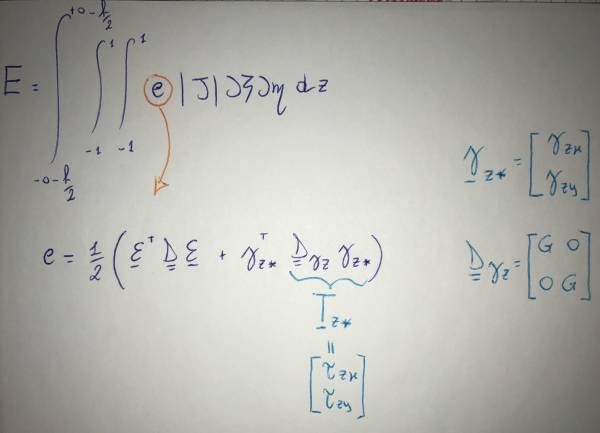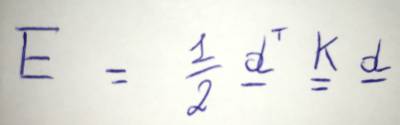Indice
Teoria delle piastre alla Kirchhoff (continuo)
Nota: le matrici ed i vettori sono indicate rispettivamente mediante doppio segno e singolo segno sotto il simbolo, ad es: $\underline{\underline{K}}$ (matrice) $\underline{k}$ (vettore).
Stato tensionale
Fatte le dovute considerazioni ( Teoria delle piastre alla kirchhoff ), siamo arrivati a definire il campo delle deformazioni per un elemento Shell:
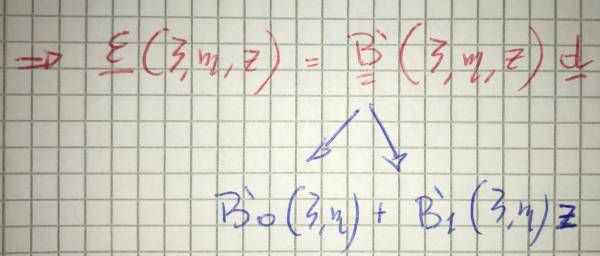
$$ \underline{\varepsilon}(x,y)= \underline{\bar{\varepsilon}}(x,y,z)+z\underline{{k}}(x,y)$$
Vogliamo risalire allo stato tensionale. Suppongo uno stato di tensione piana (vedi nota 1 a fondo pagina):
$$\sigma_{z} = 0$$
$$\varepsilon_{z}= - \nu (\varepsilon_{x} + \varepsilon_{y})$$
La matrice che correla lo stato tensionale e lo stato di deformazione è la matrice di legame costitutivo $\underline{\underline{D}}$.
$$\underline{\sigma} = \underline{\underline{D}} \underline{\varepsilon}$$
Per i materiaali isotropi, la formulazione della matrice di legame costitutivo è la seguente:
$$\underline{\underline{D}} = \frac{E}{1-\nu ^{2}} \begin{bmatrix} 1 & 0 & \nu \\ \nu & 1 & 0 \\ 0 & 0 & \frac{1-\nu}{2} \end{bmatrix} $$
A questo punto, la trattazione si potrebbe biforcare in base all'omogeneità o meno del materiale in quanto potrei avere materiali, come laminati compositi, che non hanno omogeneità di materiale lungo lo spessore e per i quali la matrice di legame costitutivo non è quindi costante ma varia con zeta $\underline{\underline{D}}(z)$
Per via generale si può quindi scrivere che:
$$\underline{\sigma} = \underline{\underline{D}}(z) \underline{\bar{\varepsilon}}(x,y,z) + z \underline{\underline{D}}(z) \underline{{k}}(x,y)$$
Da qui si osserva che, se la matrice di legame costitutivo risultasse essere costante, allora anche le tensioni così come le deformazioni risultato essere lineari in z.
Caratteristiche di sollecitazione
Posso ricavare ora le caratteristiche di sollecitazione tramite un'operazione di integrazione opportuna delle 3 componenti di tensione sulla sezione (analogamente a quanto visto in teoria della trave).
E' possibile classificare le sollecitazioni in due tipi:
- Azioni membranali (compiono lavoro sugli allungamenti del piano medio)
- Azioni flesso-torsionali
Per poterle analizzare è necessario introdurre il flusso degli sforzi e il flusso dei momenti:
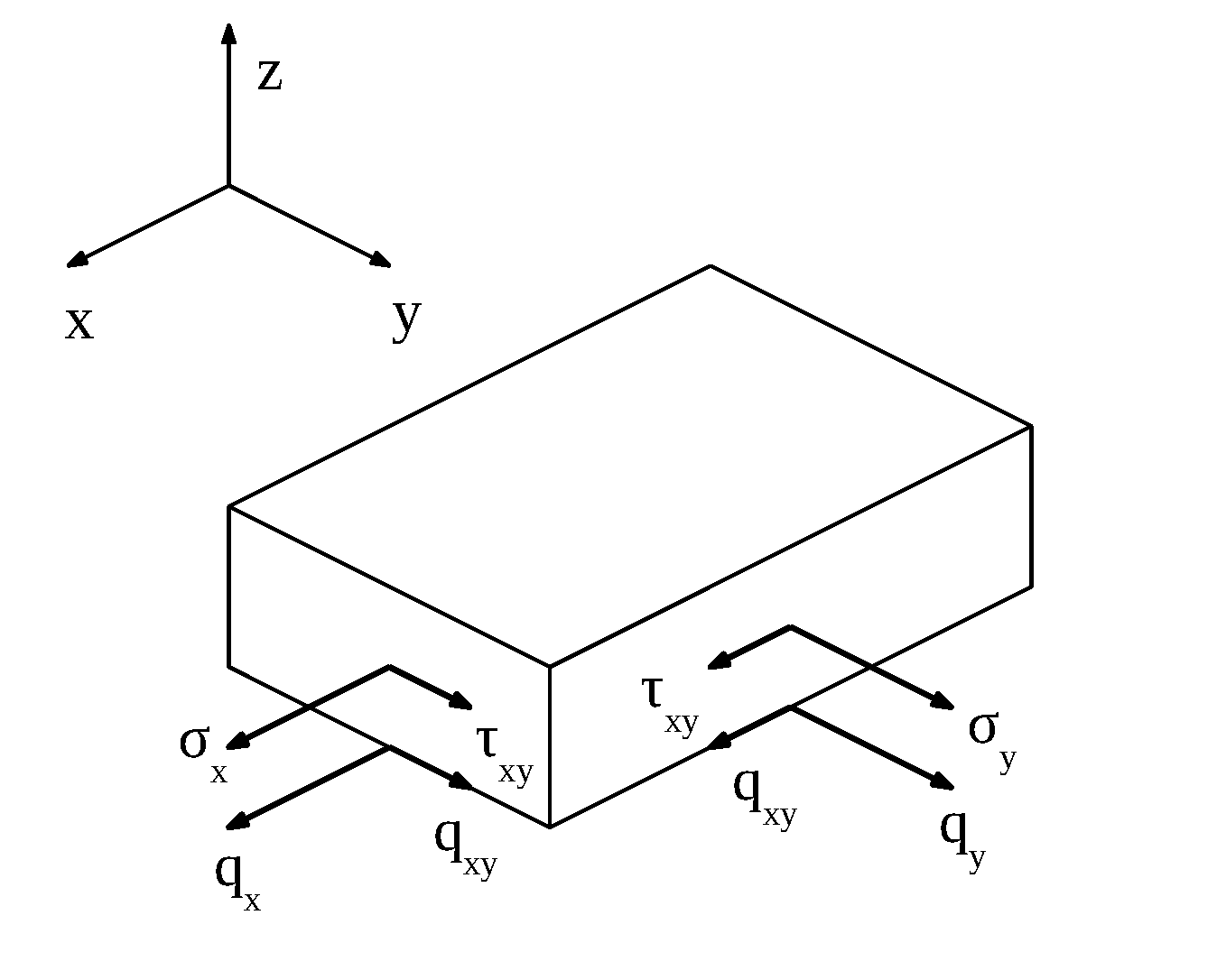
FLUSSO DEGLI SFORZI
Corrispondono agli sforzi normali e sforzo di taglio entropiano ma definiti per unità di larghezza
$$q_{x} =\int_{\frac{-h}{2}+offset}^{\frac{h}{2}+offset}{\sigma_{x}dz *1}$$
$$q_{y} =\int_{\frac{-h}{2}+offset}^{\frac{h}{2}+offset}{\sigma_{y}dz *1}$$
$$q_{xy} =\int_{\frac{-h}{2}+offset}^{\frac{h}{2}+offset}{\tau_{xy}dz *1}$$
FLUSSO DI MOMENTO:
$$m_{x} =\int_{\frac{-h}{2}+offset}^{\frac{h}{2}+offset}{\sigma_{x} z dz *1 }$$
$$m_{y} =\int_{\frac{-h}{2}+offset}^{\frac{h}{2}+offset}{\sigma_{y} z dz *1}$$
$$m_{xy} =\int_{\frac{-h}{2}+offset}^{\frac{h}{2}+offset}{\tau_{xy} z dz *1}$$
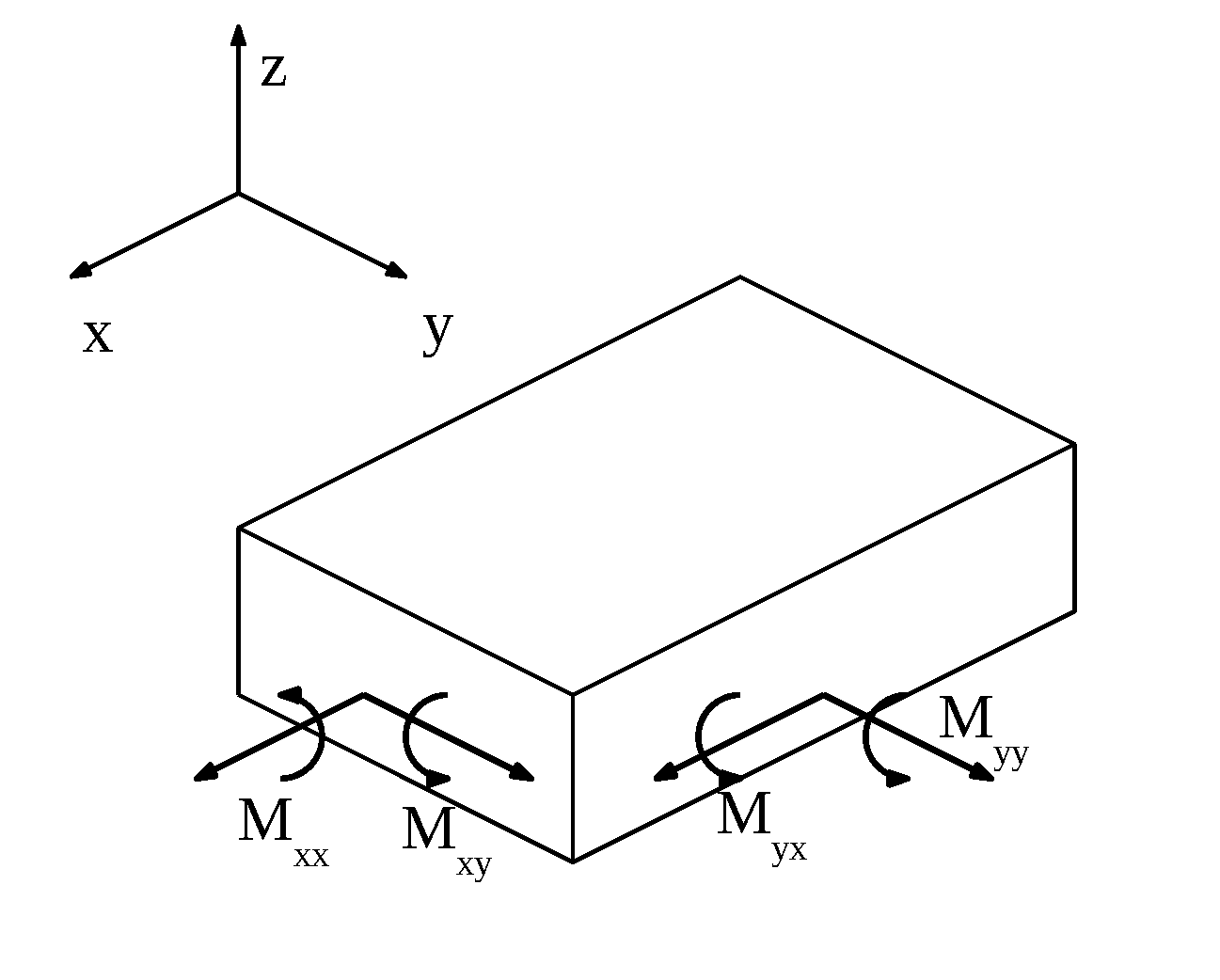
Ora ricaviamo da queste quantità i momenti agenti sulle facce degli elementi della piastra, orientati secondo gli assi del sistema di riferimento.
$m_x=M_{xy}$
$-m_{xy}=M_{xx}$
$-m_y=M_{yx}$
$m_{xy}=M_{yy}$
Dove con Mij si indica il momento applicato alla faccia ortogonale all’asse i, diretto secondo la direzione j.
Si nota dalle figure che i contributi Mxy e Myx sono FLESSIONALI, mentre Mxx e Myy esprimono contributi TORSIONALI.
In modo immediato si trovano le forze normali e taglianti:
$q_x= N_x$
$q_y= N_y$
$q_{xy}= T_{xy}$
E' quindi possibile scrivere il tutto in forma matriciale ed ottenere che:
$$\underline{q} = \begin{bmatrix} q_{x} \\ q_{y} \\ q_{xy} \end{bmatrix}= \int_{\mathrm{spessore}}{\underline{\sigma} dz } = \int_{\mathrm{spessore}}{\underline{\underline{D}}(z) \underline{\bar{\varepsilon}}(x,y,z) dz } + \int_{\mathrm{spessore}}{z \underline{\underline{D}}(z) \underline{{k}}(x,y) dz } $$
$$\underline{m} = \begin{bmatrix} m_{x} \\ m_{y} \\ m_{xy} \end{bmatrix}= \int_{\mathrm{spessore}}{\underline{\sigma} z dz } = \int_{\mathrm{spessore}}{\underline{z \underline{D}}(z) \underline{\bar{\varepsilon}}(x,y,z) dz } + \int_{\mathrm{spessore}}{z^2 \underline{\underline{D}}(z) \underline{{k}}(x,y) dz } $$
Osservando che il vettore $\underline{\bar{\varepsilon}}(x,y,z)$ delle deformazioni membranali ed il vettore curvatura $ \underline{{k}}(x,y)$ risultano non essere dipendenti da z, allora:
$$\underline{q} = \underline{\underline{A}} {\underline{\bar{\varepsilon}}} + \underline{\underline{B}} {\underline{k}}$$
$$\underline{m} = \underline{\underline{B^{T}}} {\underline{\bar{\varepsilon}}} + \underline{\underline{C}} {\underline{k}}$$
dove la matrice:
$A$ è il contributo di $\underline{\bar{\varepsilon}}$ nel definite $\underline{q}$
$B$ è il contributo di $\underline{k}$ nel definite $\underline{q}$
$B^{T}$ è il contributo di $\underline{\bar{\varepsilon}}$ nel definite $\underline{m}$
$C$ è il contributo di $\underline{k}$ nel definite $\underline{m}$
Tali matrici mediano l'influenza del vettore di deformazione membranale e del vettore curvatura sulle caratteristiche di sollecitazione
Pertanto:
$$\begin{bmatrix} \underline{q} \\ \underline{m} \end{bmatrix} = \begin{bmatrix} \underline{\underline{A}} & \underline{\underline{B}} \\ \underline{\underline{B^{T}}} & \underline{\underline{C}} \end{bmatrix} \begin{bmatrix} \underline{\bar{\varepsilon}} \\ \underline{k} \end{bmatrix}$$
FACCIAMO ORA ALCUNE IPOTESI SEMPLIFICATIVE:
- materiale omogeneo in z (non sono presenti porzioni snervate di materiale)
- offset nullo
sulla base di queste avrò che:
$$\underline{\underline{B}} = 0 = \underline{\underline{B^{T}}}$$
$$\underline{\underline{A}} = \underline{\underline{D}} h $$
$$\underline{\underline{C}} = \underline{\underline{D}} \frac{h^3}{12} $$
dove $h$ è lo spessore dell'elemento Shell.
Pertanto:
$$\begin{bmatrix} \underline{q} \\ \underline{m} \end{bmatrix} = \begin{bmatrix} \underline{\underline{D}} h & 0 \\ 0 & \underline{\underline{D}} \frac{h^3}{12} \end{bmatrix} \begin{bmatrix} \underline{\bar{\varepsilon}} \\ \underline{k} \end{bmatrix}$$
E' importante osservare che in queste ipotesi c'è disaccoppiamento tra azioni membranali e deformazioni flessionali e tra azioni flessionali e deformazioni membranali. Pertanto in questo caso particolare non sono presenti influenze miste che invece risulterebbero esserci nel caso più generale.
Sotto le ipotesi succitate, il rapporto tra le azioni membranali e le deformazioni membranali rappresenta la rigidezza dell'elemento Shell alle sollecitazioni membranali, mente, il rapporto tra le azioni flessionali e le deformazioni flessionali rappresenta la rigidezza flessionale.
La rigidezza membranale è proporzionale allo spessore. Ciò comporta che se sollecitassi membranalmente una lamina otterrei che l'allungamento che si ottiene è inversamente proporzionale allo spessore. Pertanto se avessi una cedevolezza eccessiva di un elemento Shell (isotropo ed omogeneo in z) che lavora membranalmente e supera il limite ammissibile di un fattore $\alpha$, allora, per rientrare nel range di accettabilità, devo aumentare lo spessore di almeno un fattore $\alpha$.
La rigidezza flessionale invece è proporzionale al cubo dello spessore. Ciò comporta che se sollecitassi flessionalmente un corpo a parete sottile ottenendo una cedevolezza che supera il limite ammissibile di un fattore $\alpha$, allora, per rientrare nel range di accettabilità, devo aumentare lo spessore di almeno un fattore $\alpha^{1/3}$.
OSS: Per quanto concerne lo stato tensionale, avrei che le $\underline{\sigma}$ variano in maniera inversamente proporzionale allo spessore se ho a che fare con azioni membranali, in maniera inversamente proporzionale al quadrato dello spessore se ho a che fare con azioni flessionali (c'è una elevazione al quadrato e non al cubo causa semplificazione con il braccio z nelle espressioni analitiche). Pertanto se avessi un eccesso di tensione di un fattore $\alpha$ rispetto alla tensione ammissibile, allora, per rientrare nel range di accettabilità, devo aumentare lo spessore di un fattore pari ad $\alpha$ nel caso di caricamento membranale e devo aumentare lo spessore di un fattore pari ad $\alpha^{1/2}$ nel caso di caricamento flessionale.
— NICOLÒ MARIA DELLA VENTURA 2017/05/25 11:10
Elemento piastra isoparametrico 4 nodi (element 75 in Marc)
In MARC l'implementazione standard della piastra avviene attraverso L'ELEMENT 75.
Questo è un elemento 4 nodi thick shell (piastra alla Mindlin con deformazione tagliante inclusa) i cui g.d.l nodali sono gli spostamenti e le rotazioni implicitamente intese come quantità indipendenti. Difatti si ha una interpolazione lineare per le coordinate e una bilineare sia per gli spostamenti che per le rotazioni. Dall'interpolazione delle rotazioni nodali si ottengono le rotazioni entro l'elemento, mentre dall'interpolazione degli spostamenti nodali si ottengono gli spostamenti entro l'elemento. Le deformazioni membranali sono ottenute dal campo degli spostamenti, ciò vuol dire che le rotazioni sono totalmente disaccoppiate dalle deformazioni membranali, le curvature invece sono ottenute dal campo delle rotazioni che quindi risultano totalmente disaccoppiate dagli spostamenti nodali.
La geometria di base dell'element 75 è la seguente:
$\underline{v1}$,$\underline{v2}$,$\underline{v3}$ sono le coordinate del sistema di riferimento locale, mentre ${x}$, ${y}$, ${z}$ sono le coordinate del sistema di riferimento globale.
I gradi di libertà sono ${u}$, ${v}$, ${w}$, $\phi_{x}$, $\phi_{y}$, $\phi_{z}$ , dove $\phi_{z}$ non rappresenta il moto di drilling in quanto è riferito un sistema globale.
Consideriamo con:
r: le rotazioni attorno ad ${x}$;
s: le rotazioni attorno ad ${y}$.
Funzioni di interpolazione nodali
per $i=1\ldots4$
$$ N_{i}(\xi,\eta)=\frac{1}{4}\left(1 \pm \xi \right)\left(1 \pm \eta \right) $$
Interpolazione di coordinate, spostamenti, rotazioni $$ f(\xi,\eta)=\sum_i N_i(\xi,\eta) f_i = \mathrm{N} (\xi,\eta) \; \mathrm{f} $$ ove $\mathrm{N}(\xi,\eta)$ è un vettore riga, $\mathrm{f}$ è un vettore colonna di termini $f_i$ che possono essere
- $x_i$, $y_i$, $z_i$ coordinate nodali in un sistema di riferimento $Cxyz$ fisico ma locale, ossia rototraslato rispetto ad un sistema $OXYZ$ globale al fine di portare la direzione $z$ locale ad essere normale all'elemento 1)
- $u_i$, $v_i$, $w_i$ spostamenti nodali rispetto agli assi $xyz$;
- $\theta_{x,i} \equiv \theta_i \equiv r_i$, $\theta_{y,i} \equiv \phi_i \equiv s_i$, rotazioni nodali rispetto agli assi $xy$;
Le funzioni spostamento $u(\xi,\eta)$,$v(\xi,\eta)$ e $w(\xi,\eta)$ sono riferite ai punti sul piano di riferimento.
Operatore differenziale per funzioni spostamento e rotazioni
Operatore differenziale a partire da valori nodali $f_i$ di una funzione, $i= 1\ldots n$ con $n$ numero di nodi ovvero numero di funzioni di forma
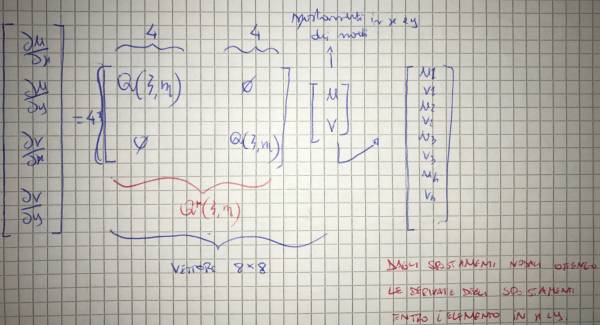
$$ \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} = \underbrace{ \begin{bmatrix} \frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} \\ \frac{\partial x}{\partial \eta} &\frac{\partial y}{\partial \eta} \end{bmatrix}^{-1} \begin{bmatrix} \cdots & \frac{\partial N_i}{\partial \xi} & \cdots \\ \cdots & \frac{\partial N_i}{\partial \eta}& \cdots \end{bmatrix} }_{\mathrm{Q}(\xi,\eta)} \begin{bmatrix} \vdots \\ f_i \\ \vdots \end{bmatrix} =\mathrm{Q}(\xi,\eta) \mathrm{f} $$
dove $\mathrm{Q}(\xi,\eta)$ è un operatore che trasforma i valori di una funzione ai nodi (spostamento o rotazione) in derivate della stessa in ${x}$ e ${y}$, risulta essere funzione di (${\xi}$, ${\eta}$) e non varia lungo lo spessore in quanto le funzioni di forma non sono definite lungo il 3° g.d.l.
Notiamo che la matrice jacobiana può essere definita sulla base di
$$ \begin{bmatrix} \frac{\partial x}{\partial \xi} \\ \frac{\partial x}{\partial \eta} \end{bmatrix} = \begin{bmatrix} \cdots & \frac{\partial N_i}{\partial \xi} & \cdots \\ \cdots & \frac{\partial N_i}{\partial \eta}& \cdots \end{bmatrix} \mathrm{x} , \quad \begin{bmatrix} \frac{\partial y}{\partial \xi} \\ \frac{\partial y}{\partial \eta} \end{bmatrix} = \begin{bmatrix} \cdots & \frac{\partial N_i}{\partial \xi} & \cdots \\ \cdots & \frac{\partial N_i}{\partial \eta}& \cdots \end{bmatrix} \mathrm{y} $$
Si può definire per blocchi
$$ \begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial y} \end{bmatrix} = \underbrace{ \begin{bmatrix} \mathrm{Q}(\xi,\eta) && \mathrm{0} \\ \mathrm{0} && \mathrm{Q}(\xi,\eta) \end{bmatrix} }_{\mathrm{Q}^\ast (\xi,\eta)} \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \end{bmatrix} $$ ove $\mathrm{u}$ e $\mathrm{v}$ sono vettori colonna contenenti gli $n$ spostamenti nodali $u_i$ e $v_i$.
Componenti di deformazione membranale e della curvatura
Poiché le componenti membranali di deformazioni sono definite sulla base degli spostamenti al piano di riferimento abbiamo
$$ \begin{bmatrix} \bar{\epsilon}_x \\ \bar{\epsilon}_y \\ \bar{\gamma}_{xy} \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 && 0 && 0 && 0 \\ 0 && 0 && 0 && 1 \\ 0 && 1 && 1 && 0 \end{bmatrix} }_{\mathrm{H}^\prime} \begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial y} \end{bmatrix} = \mathrm{H}^\prime \mathrm{Q}^\ast (\xi,\eta) \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \end{bmatrix} $$
Le componenti di curvatura sono invece definite sulla base delle sole rotazioni (e non delle di $w$), da cui
$$ \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} = \underbrace{ \begin{bmatrix} 0 && 0 && +1 && 0 \\ 0 && -1 && 0 && 0 \\ -1 && 0 && 0 && +1 \end{bmatrix} }_{\mathrm{H}^{\prime\prime}} \begin{bmatrix} \frac{\partial r}{\partial x} \\ \frac{\partial r}{\partial y} \\ \frac{\partial s}{\partial x} \\ \frac{\partial s}{\partial y} \end{bmatrix} = \mathrm{H}^{\prime\prime} \mathrm{Q}^\ast (\xi,\eta) \begin{bmatrix} \mathrm{r} \\ \mathrm{s} \end{bmatrix} $$
Componenti di deformazione membranale e della curvatura
Poiché le componenti membranali di deformazioni sono definite sulla base degli spostamenti al piano di riferimento abbiamo
$$ \begin{bmatrix} \bar{\epsilon}_x \\ \bar{\epsilon}_y \\ \bar{\gamma}_{xy} \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 && 0 && 0 && 0 \\ 0 && 0 && 0 && 1 \\ 0 && 1 && 1 && 0 \end{bmatrix} }_{\mathrm{H}^\prime} \begin{bmatrix} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial y} \end{bmatrix} = \mathrm{H}^\prime \mathrm{Q}^\ast (\xi,\eta) \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \end{bmatrix} $$
Le componenti di curvatura sono invece definite sulla base delle sole rotazioni (e non delle di $w$), da cui
$$ \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} = \underbrace{ \begin{bmatrix} 0 && 0 && +1 && 0 \\ 0 && -1 && 0 && 0 \\ -1 && 0 && 0 && +1 \end{bmatrix} }_{\mathrm{H}^{\prime\prime}} \begin{bmatrix} \frac{\partial r}{\partial x} \\ \frac{\partial r}{\partial y} \\ \frac{\partial s}{\partial x} \\ \frac{\partial s}{\partial y} \end{bmatrix} = \mathrm{H}^{\prime\prime} \mathrm{Q}^\ast (\xi,\eta) \begin{bmatrix} \mathrm{r} \\ \mathrm{s} \end{bmatrix} $$
Componenti di deformazione entro piano
Nota quindi la relazione
$$ \underline{\epsilon}(\xi,\eta,z)=\underline{\bar{\epsilon}}(\xi,\eta) + z \underline{\kappa} (\xi,\eta) $$
valida per le componenti di deformazione entro piano al generico punto P
$$ \underline{\epsilon}= \begin{bmatrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{bmatrix} $$
definite in funzione delle componenti (entro piano) di deformazione al punto Q, proiezione di P sul piano di riferimento ($z=0$ in Q)
$$ \underline{\bar{\epsilon}}= \begin{bmatrix} \bar{\epsilon}_x \\ \bar{\epsilon}_y \\ \bar{\gamma}_{xy} \end{bmatrix} $$
e delle curvature locali
$$ \underline{\kappa}= \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} $$
Notiamo che mancano le componenti fuori piano $\epsilon_z, \gamma_{zx}, \gamma_{yz}$ che normalmente caratterizzano lo stato deformativo di un punto entro un corpo deformabile.
possiamo definire per blocchi (1° blocco: 3×8, 2° blocco: 3×4, 3° blocco: 3×8) una matrice $\mathrm{B}^\prime(\xi,\eta,z)$ 3×20 di legame spostamenti - deformazioni
Abbiamo 20 gradi di libertà in quanto non consideriamo in moto di drilling, ovvero la rotazione normale al piano di piastra.
Si noti che che il 3° blocco è scalato di per ${z}$, quindi esiste una porzione della matrice che è scalata linearmente per ${z}$ e una che invece è costante in ${z}$.
Possiamo anche scrivere:
In questa forma si mette in evidenza la dipendenza lineare da ${z}$, utile per l'integrazione.
Componenti di deformazione tagliante fuori piano
Le componenti di deformazione $\gamma_{yz}$ e $\gamma_{zx}$ possono essere definite sulla base dello scostamento tra le derivate in $x,y$ dello spostamento normale al piano $w$ e le componenti di rotazione $r,s$; in particolare
$$ \gamma_{yz}= \frac{\partial w}{\partial y} - r, \quad \gamma_{zx}= \frac{\partial w}{\partial x} + s $$
da cui
$$ \begin{bmatrix} \gamma_{zx} \\ \gamma_{yz} \end{bmatrix} = \mathrm{Q} (\xi,\eta) \mathrm{w} + \begin{bmatrix} 0 & +\mathrm{N}(\xi,\eta) \\ -\mathrm{N}(\xi,\eta) & 0 \end{bmatrix} \begin{bmatrix} \mathrm{r} \\ \mathrm{s} \end{bmatrix} $$
ovvero
$$ \begin{bmatrix} \gamma_{zx} \\ \gamma_{yz} \end{bmatrix} = \underbrace{ \begin{bmatrix} \mathrm{0} & \mathrm{0} & \mathrm{Q} (\xi,\eta) & \begin{matrix} 0 \\-\mathrm{N}(\xi,\eta) \end{matrix} & \begin{matrix} \mathrm{N}(\xi,\eta) \\ 0 \end{matrix} \end{bmatrix} }_{\mathrm{B}^{\prime\prime} (\xi,\eta)} \begin{bmatrix} \mathrm{u} \\ \mathrm{v} \\ \mathrm{w} \\ \mathrm{r} \\ \mathrm{s} \end{bmatrix}= \mathrm{B}^{\prime\prime} (\xi,\eta) \; \mathrm{d} $$
con $\mathrm{B}^{\prime\prime}$ è definita per affiancamento di 5 blocchi 2×4.
A questo punto ho che:
Ma se le ${\gamma}$ sono costanti sull'elemento allora anche le ${\tau}$ dovrebbero esserlo dal momento che sono proporzionali alle ${\gamma}$. Tuttavia ${\tau}$ fuori piano non possono essere costanti sull'elemento perché le superfici TOP e BOTTOM sono superfici libere. Quindi, facendo un'analisi più dettagliata, nel caso ci fosse applicata una ${\tau}$ costante allora i due quadratini elementari agli angoli non sarebbero equilibrati alla rotazione per cui verrebbe richiamata una ${\tau}$ sulle superfici TOP e BOTTOM che violerebbe il concetto di bordo libero.
Nella teoria della trave o della piastra, se il materiale è uniforme, si suppone che le ${\tau}$ abbiano un andamento di tipo parabolico.
Il MARC gestisce questa cosa attraverso il parametro TSHEAR:
di default la distribuzione tagliante trasversa (rispetto al piano di taglio) attraverso lo spessore è costante (per le THICK SHELL).
Quindi di default il MARC considera le ${\gamma}$ in forma costante e non in continuità con il bordo libero, mentre inserendo il parametro TSHEAR inserisce una distribuzione parabolica.
Ora andiamo a scrivere l'energia potenziale elastica sull'elemento:
Sostituendo le varie definizioni:
Nel caso di piastre alla Kirchhoff è presente solo il primo integrale, mentre nel caso di piastre alla Mindlin si aggiunge anche il secondo integrale.
A questo punto, dall'uguaglianza con i lavori esterni, si ottiene:
da cui la matrice di rigidezza:
L'integrando è un polinomio di secondo grado in ${z}$, per cui per integrarlo basterebbe una regola di quadratura gaussiana a 2 punti. Il problema è che così facendo si campionerebbero gli stress a 2 punti intermedi e non dove le tensioni sono massime, ovvero al TOP e al BOTTOM.
Per tale motivo l'integrazione in ${z}$ viene effettuata seguendo la Regola di Simpson lungo lo spessore.
Regola di Simpson
La regola di Simpson prevede di campionare gli stress in 3 punti (TOP, BOTTOM e ad un punto mediano):
Da questi 3 punti si ricava una parabola e e si chiama “approssimazione dell'integrale lungo lo spessore” l'area sottesa alla parabola della quantità d'interesse.
Per problemi lineari si può utilizzare la regola di Simpson a un punto interno (3 in totale: uno mediano e due sulle superfici), mentre per casi non lineari i punti di campionamento possono essere anche 7 o 11.
Per quanto riguarda l'integrazione in ${\xi}$ ed ${\eta}$ entro piano si campiona nei 4 punti di Gauss come nel caso dell'isoparametrico 4 nodi.
Per essere più precisi i punti di integrazione possiamo immaginarli come i seguenti:
Il contributo legato alle deformazioni fuori piano (presente solo nel caso di piastre alla Mindlin) potrebbe essere svolto in maniera diversa in quanto presenta il problema dello Shear Locking.
Lo Shear Locking deriva dal fatto che quello che dovrebbe essere uno stato di curvatura uniforme viene in realtà rappresentato con una deformazione trapezia. La deformazione trapezia, in corrispondenza dei 2 punti di Guass (se ne uso 2 per asse), mi dà una deformazione tagliante spuria che in quella esatta non è presente.
Una delle gestioni tipiche del problema dello shear locking è andare a campionare le deformazioni taglianti nel singolo punto di Gauss invece che ai 2 classici, in questo modo quel punto di Gauss finisce in punto che a curvatura uniforme vede una ${\gamma}$ nulla. Campionare in un solo punto di Gauss per asse vuol dire utilizzare un punto in meno per asse di quelli necessari per avere soluzione esatta nel caso di Jacobiano uniforme.
Integrando a un solo punto di Gauss per asse invece che a due si risolve il problema dello Shear Locking. Per tale motivo nei FEM lineari si sceglie di implementare il calcolo della matrice di rigidezza andando a svolgere un integrale nei 4 punti di Gauss e l'altro integrale in un solo punto di Gauss (sfruttando sempre la regola di Simpson).
In questo modo si ha un sistema sottointegrato che non soffre del problema dello Shear Locking.
— FIOCCHETTI ALESSANDRO 2017/05/25 21:30
Modi di deformazione elementari di un elemento piastra alla Mindlin
Fino ad ora l'elemento piastra (4 nodi) l'abbiamo considerato caratterizzato da 20 gdl (5 per ogni nodo), in quanto non è contemplata la rotazione $\phi_{z}4 attorno all'asse perpendicolare al piano di maggior estensione della piastra (moto di Drilling). Vedi element 75 nella guida al Marc.
Quando però esprimo tutto in termini di coordinate globali avrò che nessun asse globale è perfettamente perpendicolare alla superficie di massima estensione della piastra. Sostanzialmente quindi un elemento piastra, per come è effettivamente implementato, avrà 6 gdl e non 5 in quanto non posso escludere nessuna delle tre rotazioni globali (al più si potrebbe escludere la composizione delle rotazioni globali ma non è una operazione che è solito adottare).
Quindi ogni elemento piastra ha 6 gdl per nodo. Ciò comporta che se posso definire delle deformazioni base dell'elemento piastra, componendo le quali ottengo tutte le possibili deformazioni, avrei 24 deformazioni elementari:
Questi sono 24 modi deformativi elementari associati però a composizioni speciali dei valori di spostamento sui 24 gdl. Potrei spostare uno alla volta ogni singolo gdl tenendo fermi gli altri ma non otterrei deformazioni interessanti.
Quindi, nella Figura sopra riportata, abbiamo 24 deformazioni base generate da composizioni speciali dei valori di spostamento dei 24 gdl.
Tra di questa abbiamo:
- 6 moti di corpo rigido (4a colonna in Figura)
- 4 moti di Drilling associati a ciascun nodo (ultimi tre modi deformativi della 3a colonna in Figura). Non tutti gli elementi implementati nel Marc presentano questi 4 moti deformativi elementari (si veda ad esempio l'elemento Solid Shell per il quale queste 4 deformazioni sono sostituite con i 4 moti di schiacchiamento in direzione z dei 4 nodi)
- 2 deformazioni trapezie associate a moti puramente flessionali (modi deformativi 1 e 2 in Figura). Nel caso di piastra alla Kirchhoff avremmo una deformazione cubica e non trapezia.
- 3 deformazioni associate a moti puramente taglianti fuori piano ( $\gamma_{xz}$ e $\gamma_{yz}$ ). Per essi i segmenti estremali rimangono verticali → non ruotano ma traslano solamente in z (4°, 5° e 7° modo deformativo in Figura). In Kirchhoff tali modi di deformazione dell'elemento piastra non sono contemplati in quanto nella teoria alla Kirchhoff si assume sin da subito che le deformazioni taglianti fuori piano sono nulle
- 1 deformazione associata a moto puramente tagliante ENTROPIANO $\varepsilon_{xy}$ uniforme lungo lo spessore (13° modo deformativo in Figura)
- 2 deformazioni taglianti trapezie entropiano (modi deformativi 8 e 9 in Figura)
- 1 allungamento in direzione x per il quale avrei $\varepsilon_{x} > 0$ ovunque (9° modo deformativo in Figura)
- 1 allungamento in direzione y per il quale avrei $\varepsilon_{y} > 0$ ovunque (10° modo deformativo in Figura)
- 2 deformazioni trapezie opposte tra TOP e BOTTOM (12° e 14° modo deformativo in Figura). Il 12° modo deformativo presenta una curvatura in direzione x che va da un valore negativo (TOP → si comprime/riduce) a un valore positivo (BOTTOM → allunga). Il 14° modo deformativo presenta una curvatura in direzione y che va da un valore positivo (TOP → si allunga) a un valore negativo (BOTTOM → si comprime/riduce)
- 2 deformazioni elementari che combinate tra di loro generano il moto torsionale (3° e 6° modo deformativo in Figura).
L'elemento Shell (alla Mindlin) è pertanto infinitamente rigido a qualunque moto che non sia riconducibile a questi 24 moti deformativi elementari.
Note
Nota 1
Ipotizzando uno stato di tensione piana, nel quale la deformazione $\varepsilon_{z}$ non risulta essere nulla, si entrerebbe, a rigore, in contrasto con l'aver affermato che il segmento che collega il punto Q (appartenente al piano di riferimento) ed i punti P (non appartenenti al piano di riferimento ma per i quali la proiezione su di esso è il punto Q) è rigido ( Teoria delle piastre alla kirchhoff ).
Di fronte a questa assodata incongruenza è possibile però, poiché classificata come errore di modellazione di ordine superiore, chiudere un occhio. Si potrebbe, in alternativa, utilizzare un modello a strati indipendenti per il quale ogni strato lavora in tensione piana ed essi possono distaccarsi l'uno dall'altro o compenetrarsi.
— NICOLÒ MARIA DELLA VENTURA 2017/05/25 11:05