Analisi modale
Il compito di questo tipo di analisi è quello di determinare i modi propri del sistema, ossia quei moti periodici concessi dall'equazione $$(-\omega ^2\underline{\underline{M}}+j\omega \underline{\underline{C}}+\underline{\underline{K}})\overline{x}=\overline{f}$$ anche nel caso di $\overline{f}=0$.
Spesso conviene effettuare un'analisi modale della struttura prima di compiere l'analisi in frequenza, dato che il costo computazionale è decisamente inferiore e i solutori più efficaci; inoltre, l'analisi modale potrebbe fornire informazioni sufficienti per lo scopo che si vuole raggiungere, rendendo così non necessaria la più laboriosa analisi in frequenza.
Affinchè un moto non stimolato possa perdurare nel tempo, è necessario che gli elementi dissipativi di smorzamento siano assenti $\underline{\underline{C}}=0$. L'equazione è dunque così riscrivibile:
$$ (\underline{\underline{K}} - \omega ^2\underline{\underline{M}})\overline{x} = 0$$
Le soluzioni (non banali) di questo problema derivano dalla risoluzione (ricavata attraverso algoritmi numerici) del problema agli autovalori generalizzato del tipo $det(\underline{\underline{K}}-\omega ^2\underline{\underline{M}}) = 0$ che ha come soluzione le n coppie $(\omega _{i}^2,\overline{x} _{i})$. La prima componente rappresenta il quadrato della pulsazione e la seconda rappresenta la forma di moto del modo proprio, dove per forma di moto si intende la tipologia di moto (ad es. traslazione in x) senza considerarne l'entità.
Si preferisce risolvere il problema generalizzato per evitare l'inversione della matrice $\underline{\underline{M}}$, in quanto il problema agli autovalori standard vorrebbe la risoluzione di $(\underline{\underline{M^{-1}}}\underline{\underline{K}}-\omega ^2\underline{\underline{I}})\overline{x} = 0$. Nonostante $\underline{\underline{M}}$ sia sempre non singolare e quindi ammetta sempre una sua inversa, risolvendo il problema generalizzato risparmiamo memoria computazionale.
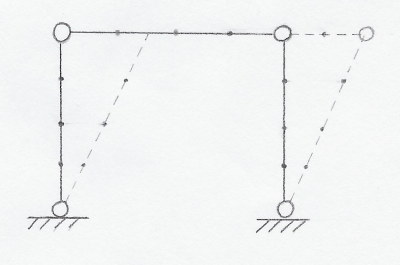
Esempio di moto per $\omega=0$
Le soluzioni $\omega=0$ del problema agli autovalori generalizzato rappresentano moti a cui non corrisponde una reazione elastica, quindi saranno moti di corpo rigido o moti di meccanismo.
Per esempio, per il quadrilatero articolato riportato sopra, si trova che la più bassa pulsazione propria del sistema è, appunto, $\omega=0$; a tale pulsazione, per piccoli spostamenti, si associa il moto di deformazione a parallelogramma riportato in figura.
Questa nozione può essere utile nel caso in cui ci troviamo ad analizzare una struttura che risulta labile, ma non riusciamo a capire dove risieda tale labilità. In casi del genere, possiamo andare a calcolarci i primi modi propri della struttura e, se uno di questi equivale a $\omega=0$ (o comunque $\omega$ uguale a un valore molto piccolo - dell'ordine di $10^{-6}$ Hz per esempio), è probabile che, analizzando la rispettiva forma, si riesca a definire il punto in cui la struttura è labile. Nel caso in esame, la labilità verrebbe evidenziata dalla forma che descrive il moto di deformazione a parallelogramma, reso possibile dalla presenza delle cerniere.
Definizione dell'autovettore a meno di una costante moltiplicativa
Le coppie di soluzioni autovalore-autovettore sono definite a meno di una costante moltiplicativa arbitraria e non ci danno indicazioni sull'effettiva intensità delle risposte.
A livello di software, avviene che il solutore fornisce un valore numerico che descrive una certa forma modale e la mappa dei valori di tensione da noi richiesti (per esempio: valore della Von Mises); ma i valori di tensione dipendono dalla “ampiezza” della forma modale, la quale abbiamo detto essere definita a meno di una costante moltiplicativa. Perciò, anche le tensioni verranno a dipendere da questa costante. In sostanza, da un'analisi di questo tipo, noi potremmo andare a ricavare come dato utile NON il valore numerico del picco di tensione, bensì dove si trova il picco di tensione. Un altro dato che si può ricavare è il seguente: data una forma modale e la relativa mappatura delle tensioni, si può considerare il rapporto tra due valori di tensione in due punti distinti della struttura, in quanto il fattore di scala dell'autovettore non influisce sul rapporto.
Per riassumere il concetto: mai fare valutazioni ingegneristiche sul modulo di un autovettore.
Autovalori con molteplicità maggiore di 1
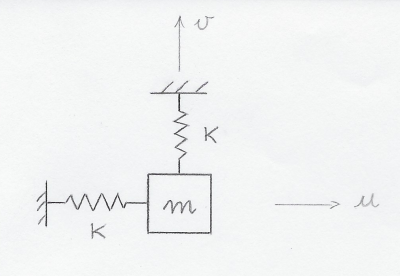
Vediamo cosa succede se l'analisi modale del sistema evidenzia la presenza di un autovalore con molteplicità maggiore di 1. Prendiamo come esempio il problema seguente:
I gradi di libertà della struttura sono u e v. I primi due modi di vibrare del sistema sono:
$\omega _{1}=\sqrt{\frac{K}{m}}$ ; $\overline{x} _{1}=(0,1)$ $[\cdot\lambda]$
$\omega _{2}=\sqrt{\frac{K}{m}}$ ; $\overline{x} _{2}=(1,0)$ $[\cdot\lambda]$
Nell'ipotesi che la costante di rigidezza K sia identica per entrambe le molle, l'autovalore è lo stesso, mentre i due autovettori descrivono rispettivamente un moto puro verticale e un moto puro orizzontale, eventualmente modulati per un'opportuna $\lambda$. Andando ad analizzare la struttura con il Marc, il solutore potrebbe restituire sia uno dei due moti singolarmente, sia una combinazione lineare dei due, del tipo:
$\overline{X}=\overline{x} _{1}\lambda _{1}+\overline{x} _{2}\lambda _{2}$
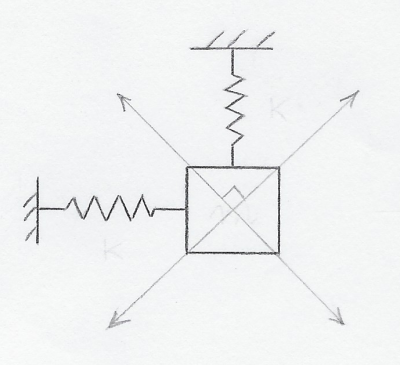
Un esempio, potrebbe essere il seguente:
In questo caso, il Marc avrebbe restituito due moti ortogonali evidentemente diversi da quelli puramente verticale e orizzontale.
In conclusione, se abbiamo molteplicità maggiori di 1 per l'autovalore, è possibile avere una composizione di forme modali.
Ad ogni modo, nella pratica è abbastanza difficile che si presentino casi di autovalori con molteplicità maggiori di 1, in quanto bastano piccole differenze, anche solo a livello di tolleranze, per avere due autovalori distinti, seppur molto vicini. In riferimento al caso in oggetto, basterebbe che la rigidezza K nelle due molle differisse di una quantità molto piccola per perdere l'uguaglianza tra le $\omega$.
Normalizzazione di un autovettore
Vediamo ora come si normalizza un autovettore. Alcuni software (tipo Ansys) utilizzano la normalizzazione definita “norma a infinito unitaria”, che consiste nel considerare il modulo dell’autovettore pari al modulo della sua componente maggiore, per poi porlo uguale a 1 e modulare tutte le altre componenti di conseguenza. Questa normalizzazione è semplice da utilizzare, ma può dare dei problemi.
Un altro tipo di normalizzazione (quella che useremo) è chiamata “normalizzazione a massa modale unitaria”: essa prevede che l’autovettore venga scalato di una quantità $\lambda$ non arbitraria, bensì tale che:
$$(\widehat{x} _{i})^{T}\underline{\underline{M}}(\widehat{x} _{i})=(\lambda\overline{x} _{i})^{T}\underline{\underline{M}}(\lambda\overline{x} _{i})=1$$
da cui si ricava
$$\lambda^{2}=\frac{1}{(\overline{x} _{i})^{T}\underline{\underline{M}}(\overline{x} _{i})}$$
E' poi interessante notare come, andando a sostituire la funzione di risposta
$$x _{i}(t)=a _{i}\widehat{x} _{i}e^{jw _{i}t}$$
all'interno dell'equazione iniziale
$$\underline{\underline{M}}\ddot{x} + \underline{\underline{C}}\dot{x} + \underline{\underline{K}}x = F(t)$$
si ottiene la forma algebrica
$$\underbrace{(\underline{\underline{K}}-\omega _{i}^{2}\underline{\underline{M}})a _{i}\widehat{x} _{i}}+j\omega _{i}\underline{\underline{C}}a _{i}\widehat{x} _{i}=\overline{f}$$
Dato che $\omega _{i}$ è un autovalore e $\widehat{x} _{i}$ l'autovettore associato, la quantità evidenziata dalla graffa sarà uguale a zero. Rimane così un'espressione nella quale il rapporto tra la forzante $\overline{f}$ e il termine che modula la soluzione $a _{i}$ è definito puramente dalla matrice smorzamento. In sostanza, si ha che quando abbiamo una forzante con pulsazione pari ad una pulsazione propria del sistema, ovvero quando siamo in condizioni di risonanza, allora il rapporto tra $\overline{f}$ e $a _{i}$ è definito dalla sola matrice C. In particolare si può ricavare la seguente espressione
$$a _{i}=\frac{1}{j\omega _{i}}\frac{\widehat{x} _{i}^{T}\overline(f)}{\widehat{x} _{i}^{T}\underline{\underline{C}}\widehat{x} _{i}}$$
ovvero l'entità del termine che modula la risposta. $a _{i}$ risulta dunque essere uguale al rapporto tra il prodotto scalare del moto proprio per la forzante (termine di accoppiamento moto/forzante) e un termine che tiene conto delle azioni smorzanti.