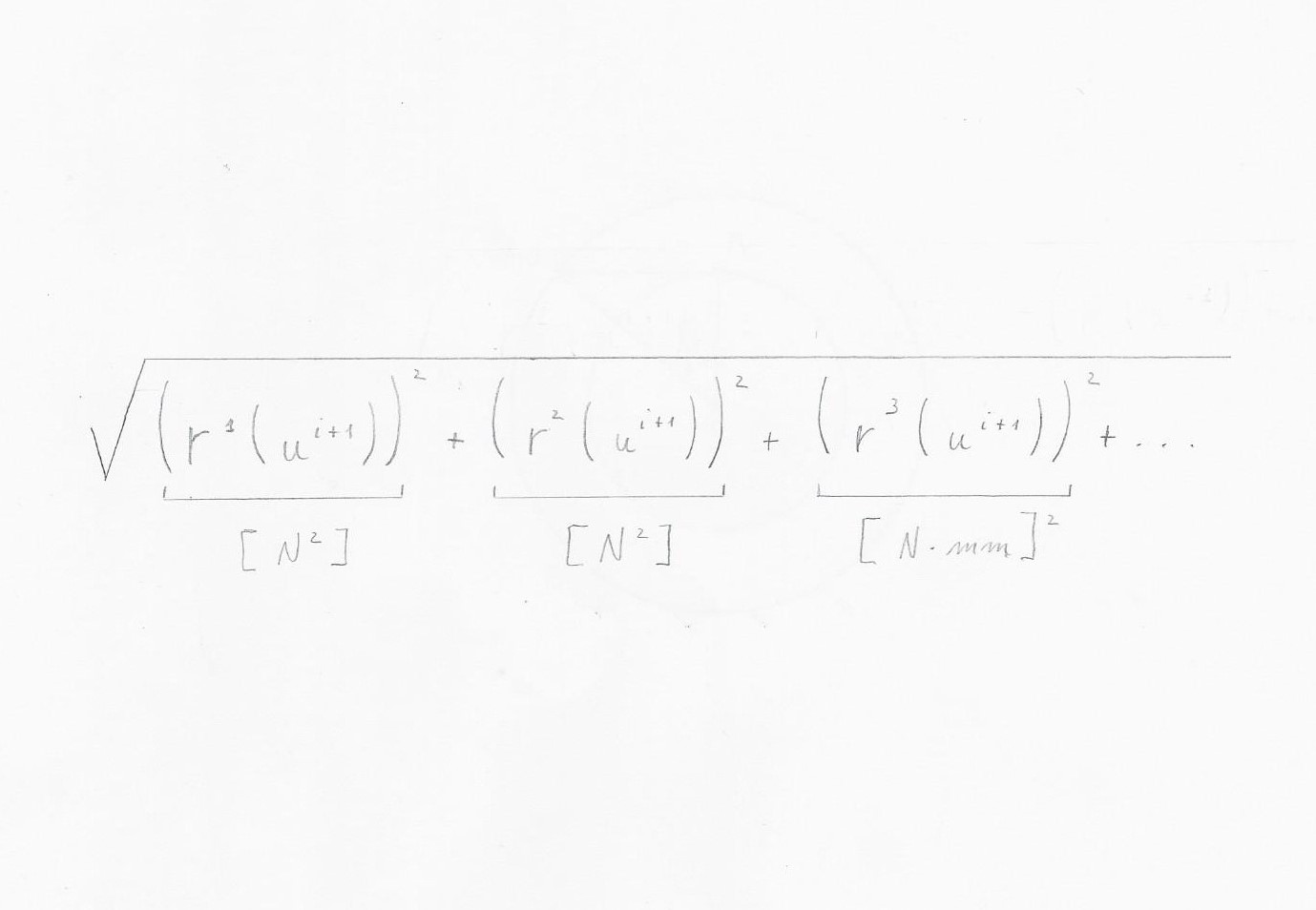I fenomeni non lineari nelle strutture sono dovuti a:

1) Non linearità geometriche

Si dividono in

• Grandi rotazioni.

Si definiscono grandi rotazioni quelle per le quali non vale l'approssimazione

$$\sin \theta \approx \theta $$ $$\cos \theta \approx 1 $$

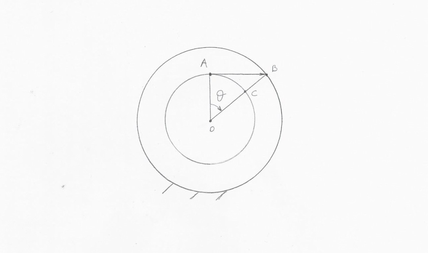
Come esempio si può considerare un perno di banco nella sua sede come in figura.

Si prenda il punto A e una generica rotazione del perno; se la rotazione è piccola si può linearizzare l'angolo con la sua tangente e quindi confondere l'arco AC con il segmento AB. Nel caso in cui la rotazione è grande, come in figura, invece non è possibile compiere questa approssimazione dal momento in cui da una situazione con gioco si passa ad una con interferenza in quanto il punto A si sposta in B.

• Grandi deformazioni

Si definiscono grandi deformazioni quelle per le quali non vale la

$$\epsilon_{x}= \frac{\partial u}{\partial x} $$

infatti in questi casi la $\varepsilon $ deformazione è definita con una funzione più complessa. E' questo il caso dei metalli in campo plastico oppure delle gomme.

2) Comportamento non lineare del materiale

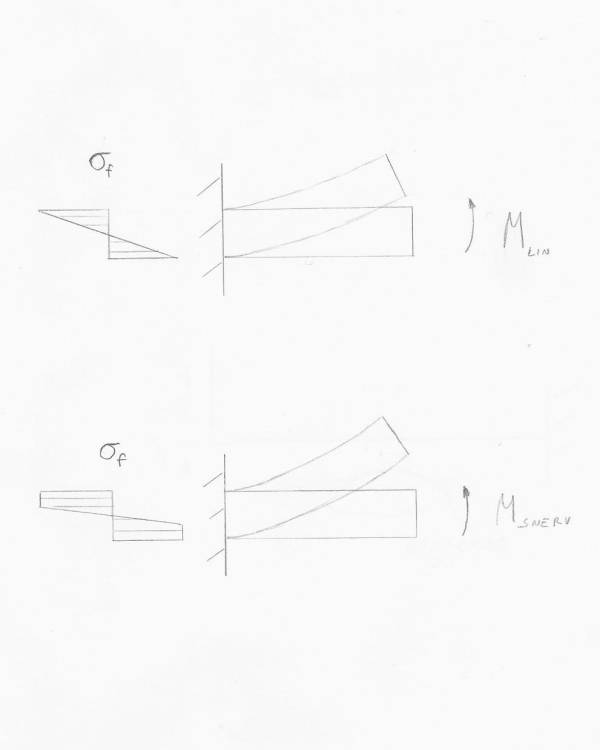
Un esempio che si può fare è la plasticizzazione di una trave sottoposta a Momento flettente come in figura. Finché le fibre più lontane dall'asse neutro hanno una $\sigma _{f}$ inferiore a quella di inizio plasticizzazione il comportamento è lineare; aumentando ancora la Coppia flettente si ha che queste fibre cominciano a snervarsi.

3) Non linearità indotta da fenomeni di contatto tra corpi

Questi fenomeni si dividono in

• con attrito

• senza attrito

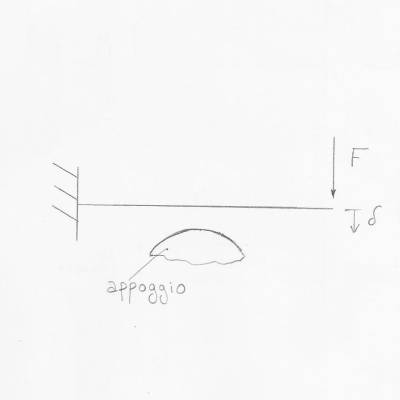
I primi devono la loro non linearità alle ovvie dissipazioni energetiche. Per quel che riguarda i secondi, invece, possiamo considerare il seguente esempio di una trave a sbalzo sotto la quale c'è un appoggio.

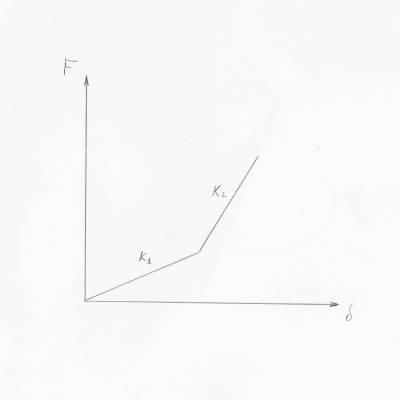
La trave si flette verso il basso: finché non entra in contatto con l'appoggio il comportamento rimane lineare ma in seguito si ha una variazione della struttura dovuta al sostegno che causa una variazione della rigidezza della struttura. In particolare un irrigidimento della stessa chiamato stiffening . Graficamente avremo

Esistono anche i casi di softening in cui invece si verifica l'effetto opposto.

Consideriamo un sistema non lineare di n equazioni $$\bar{R}\left ( \bar{u} \right )= \bar{F}\left ( \bar{u} \right )$$ nelle n componenti incognite del vettore $\bar{u}$ , con $$\bar{R}:\bar{u}\rightarrow \mathbb{R}^{n}, \bar{u}\in C\subseteq \mathbb{R}^{n}$$ $$\bar{F}:\bar{u}\rightarrow \mathbb{R}^{n}, \bar{u}\in C\subseteq \mathbb{R}^{n}$$

funzioni vettoriali di variabile vettoriale.

Nel caso specifico della soluzione di sistemi di equazioni derivate dagli equilibri nodali di strutture discretizzate con metodo FEM, ho

• $\bar{u}$ : vettore contenente le componenti di spostamento/rotazione nodale dalla configurazione indeformata (incognite);

• $\bar{F}\left ( \bar{u} \right )$ : vettore contenente le componenti di forza/coppia nodale applicate dall’esterno sul sistema, supposte note per una data configurazione della struttura;

• $\bar{R}\left ( \bar{u} \right )$ : vettore contenente le componenti di azione nodale necessarie a mantenere la struttura in equilibrio nello stato deformativo associato al vettore spostamenti nodali $\bar{u}$ ovvero vettore contenente le componenti di azione nodale associate (uguali e contrarie) alle reazioni elastiche della struttura costretta in stato deformato. Nel caso particolare di sistema elastico lineare $\bar{R}\left ( \bar{u} \right )=K\bar{u}$, con K matrice di rigidezza.

Possiamo arrivare ad una scrittura alternativa del sistema non lineare introducendo il residuo $\bar{r}\left ( \bar{u} \right )=\bar{R}\left ( \bar{u} \right )- \bar{F}\left ( \bar{u} \right )$ ; così facendo si può scrivere

$$\bar{r}\left ( \bar{u} \right )=0$$

Il metodo di N-R è costruito a partire dallo sviluppo in serie di Taylor al primo ordine di quest'equazione nell'intorno di un i-esimo punto d'iterazione $\bar{u}^{i}$ , ossia

$$\bar{r}\left ( \bar{u}^{*} \right )=\bar{r}\left ( \bar{u}^{i} \right )+J_{r}|_{\bar{u}=\bar{u}^{i}}\cdot \left ( \bar{u}^{*}-\bar{u}^{i} \right )+o\left ( \bar{u}^{*}-\bar{u}^{i} \right )=0$$

In cui $J_{r}$ è lo Jacobiano della funzione residuo r calcolato al punto $\bar{u}^{i}$ , mentre $\bar{u}^{*}$ è la soluzione esatta incognita. Trascurando l'o piccolo l'uguaglianza con 0 si perde; per riottenerla non dobbiamo più considerare la soluzione esatta bensì qualcosa che consideriamo essere l'iterato successivo $\bar{u}^{i+1}$ . Possiamo quindi scrivere

$$\bar{r}\left ( \bar{u}^{i} \right )+J_{r}|_{\bar{u}=\bar{u}^{i}}\cdot \left ( \bar{u}^{i+1}-\bar{u}^{i} \right )=0$$

da cui supponendo $J_{r}$ non singolare $$\bar{u}^{i+1}=\bar{u}^{i}-J_{r}|_{\bar{u}=\bar{u}^{i}}\setminus \bar{r}\left ( \bar{u} \right )$$

L'iterazione necessita di un punto di partenza $\bar{u}^{0}$ che, in assenza di particolari indicazioni, si prende uguale a 0.

Essendo un metodo iterativo non si arriverà mai alla soluzione esatta; occorre perciò definire dei criteri di arresto. Ne consideriamo due:

• Convergenza ai residui

L'iterazione si ferma quando la norma del residuo all'iterato considerato è minore di una certa tolleranza $ \epsilon _{r}$ $$\left \| \bar{r}\left ( \bar{u}^{i+1} \right ) \right \|< \epsilon _{r}$$

Questo criterio di convergenza presenta però due problemi. Il primo riguarda l'unità di misura di questa tolleranza: infatti se le incognite sono solo forze nodali allora r ha le dimensioni di una Forza e quindi l'unità di misura è il Newton e non si hanno problemi; se però all'interno di $\bar{u}$ oltre che spostamenti ho anche delle rotazioni allora dentro alla $\bar{F}$ e alla $\bar{R}$ non avrò solo Forze ma anche delle Coppie. Dunque la norma del residuo comprende termini disomogenei tra loro.

Quello che si può fare per aggirare il problema è dividere i termini di Coppie per una lunghezza caratteristica (anche se qui sorge la questione di definire una lunghezza caratteristica della struttura).

Il secondo riguarda il valore di $\epsilon _{r}$ nel caso di carichi autoequilibrati. Infatti se consideriamo $\epsilon _{r}$ come una grandezza caratteristica e quindi frazione di qualcosa si ha

$$ \epsilon _{r}=\lambda _{r}\cdot \bar{A}$$

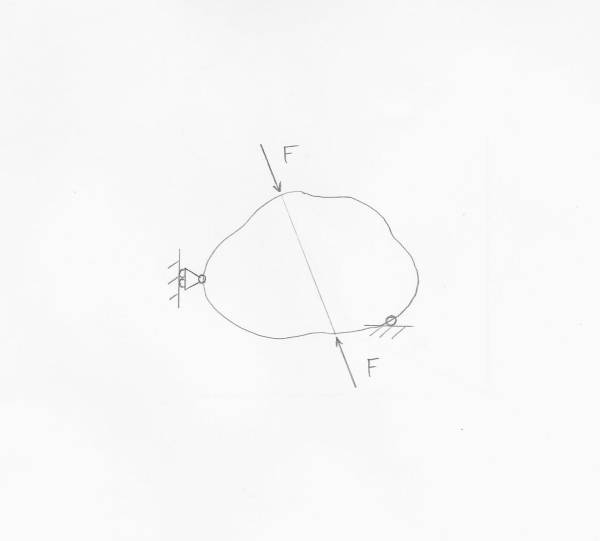
dove $\lambda _{r}$ è una costante e $\bar{A}$ è il vettore delle reazioni vincolari. Nel caso io abbia una struttura autoequilibrata come in figura

allora il vettore $\bar{A}$ sarà nullo e quindi anche la tolleranza diventerà uguale a 0. Ciò porterebbe il metodo a non arrestarsi mai in quanto non si raggiungerà mai la soluzione esatta.

• Convergenza agli spostamenti

E' chiamata “agli spostamenti” ma in realtà sono generici gdl e quindi anche rotazioni. Il metodo si arresta quando è raggiunta la condizione

$$\left \| \bar{u}^{i+1}-\bar{u}^{i} \right \|< \epsilon _{\delta }$$

dove $\epsilon _{\delta}$ è la tolleranza assoluta; in alternativa a questa si può usare anche una condizione con tolleranza relativa $\lambda _{\delta}$

$$\left \| \bar{u}^{i+1}-\bar{u}^{i} \right \|< \lambda _{\delta}\left \| \bar{u}^{i+1} \right \|$$

La relazione che lega la tolleranza assoluta con quella relativa è

$$\lambda _{\delta} \left \| \bar{u}^{i+1} \right \|=\epsilon _{\delta}$$

Qui sorge il seguente problema: a fronte di una tolleranza relativa “piccola” non è detto che anche quella assoluta lo sia. Infatti se sono ammessi moti di Corpo Rigido la norma vettoriale $\left \| \bar{u}^{i+1}-\bar{u}^{i} \right \|$ può essere tale da rendere le tolleranze anche di ordini di grandezza differenti.

Si può chiedere che siano soddisfatti entrambi i criteri di convergenza oppure anche solo uno di questi.

Appunti per il corso di Progettazione Assistita

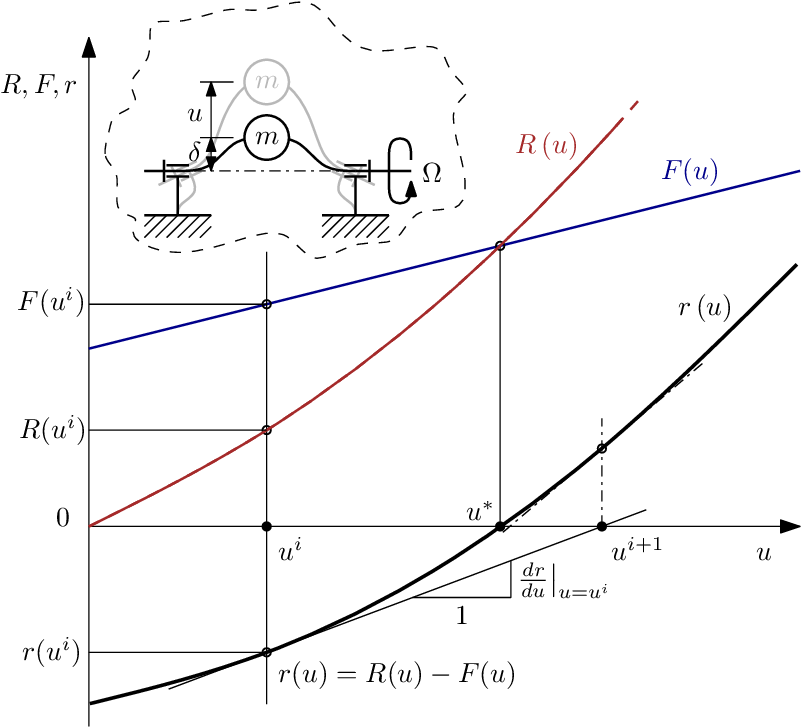
Sia u un vettore di una sola componente, perché caso monodimensionale, da considerarsi perciò uno scalare, F(u) forza funzione di uno scalare, definita dalla curva blu.

La reazione elastica della struttura è la curva in rosso R(u). La soluzione esatta corrisponde ad $u^{*}$, punto in cui le due curve si incontrano e si eguagliano. Facendo la sottrazione tra le due curve si ottiene la curva del residuo $r(u)$ in nero.

Parto da un generico $r(u^{i})$ e vado a calcolare il suo residuo definendo il punto $r(u^{i})$. In genere la curva r(u) non è data altrimenti si avrebbe già la soluzione, perciò, si calcola il residuo di $u^{i}$ che è l’unico punto visibile di tutta la curva. N-R prevede di conoscere, oltre al residuo, anche lo Jacobiano che è una matrice con tutte le derivate parziali, in questo caso, una matrice 1×1 con un unico elemento, cioè la derivata totale $\frac{\mathrm{d} r}{\mathrm{d} u}$, rappresentata graficamente tramite la pendenza della tangente. Noto il residuo e lo Jacobiano è, infatti, possibile risolvere il sistema di equazioni, associato al passo di iterazione, per via grafica, in un’unica equazione, e la soluzione non è altro che l’intersezione della retta tangente con l’asse $r(u)=0$ . Questa intersezione mi fornisce $u^{i+1}$, il successivo passo iterativo. A questo punto, è possibile ripetere la procedura partendo da questo nuovo passo.

Calcolo il residuo di $u^{i+1}$ e lo Jacobiano, cioè disegno la retta tangente, e trovo il nuovo passo successivo $u^{i+2}$ dato sempre dall’intersezione tra la retta tangente e l’asse $r(u)=0$. Ripeto l’iterazione finchè non raggiungo uno dei criteri di convergenza che ho scelto di usare.

Con riferimento alla figura sottostante si tratta il metodo di N-R applicato ad un caso bidimensionale.

Sia $\underline{r}(\underline{u})$ la funzione residuo, funzione vettoriale di componenti $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$, di variabile vettoriale $\underline{u}$, di componenti $u_{1}$ e $u_{2}$ . Il metodo di N-R si pone l’obiettivo di individuare, per via iterativa, la soluzione dell’equazione vettoriale $\underline{r}(\underline{u})=0$, rappresentativa di un sistema di 2 equazioni (nel caso in esame non lineari) in 2 variabili.

Si supponga di trovarsi all’i-esimo step di iterazione.

Nella Figura (a) sono rappresentate le due funzioni $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$ per curve di livello e la configurazione $\underline{u}_{i}$ (nota all’i-esimo step di iterazione). La soluzione che si intende avvicinare il più possibile mediante il metodo di N-R è rappresentata dal punto $\underline{u}^{*}$, per il quale $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$ si annullano.

Si tenga presente però che tali curve non sono note al risolutore, il quale conosce soltanto:

1. il valore che esse assumono in $\underline{u}^{i}$
2. il valore di tutti gli elementi della matrice Jacobiana di $\underline{r}(\underline{u})$ calcolata in $\underline{u}=\underline{u^{i}}$

Per procedere si individuano due piani, rispettivamente tangenti alle curve $r_{1}(\underline{u})$ ed $r_{2}(\underline{u})$,nella configurazione $\underline{u}_{i}$:

• $T_{1}^{i}(\underline{u})$ è tangente ad $r_{1}(\underline{u}=\underline{u}^{i})$
• $T_{2}^{i}(\underline{u})$ è tangente ad $r_{2}(\underline{u}=\underline{u}^{i})$

Nota:

Per individuare un piano sono in generale necessari tre elementi: un punto dello spazio per cui passa il piano e due coefficienti ad indicarne l’inclinazione, tutti noti per ipotesi.

Nel caso del piano $T_{1}^{i}(\underline{u})$ il punto di passaggio è $( \underline{u}^{i} , r_{1}(\underline{u}=\underline{u}^{i}) )$, ed i due coefficienti sono gli elementi della prima riga dello Jacobiano di $\underline{r}(\underline{u})$, $$\begin{bmatrix}\frac{\partial r_{1}}{\partial u_{1}} & \frac{\partial r_{1}}{\partial u_{2}} \\ \frac{\partial r_{2}}{\partial u_{1}} &\frac{\partial r_{2}}{\partial u_{2}} \end{bmatrix}$$ calcolata per $\underline{u}=\underline{u}^{i}$.

Nel caso del piano $T_{2}^{i}(\underline{u})$ il punto di passaggio è $( \underline{u}^{i} , r_{2}(\underline{u}=\underline{u}^{i}) )$, ed i due coefficienti sono gli elementi della seconda riga dello Jacobiano di $r(\underline{u})$ $$\begin{bmatrix} \frac{\partial r_{1}}{\partial u_{1}}&\frac{\partial r_{1}}{\partial u_{2}} \\ \frac{\partial r_{2}}{\partial u_{1}}&\frac{\partial r_{2}}{\partial u_{2}} \end{bmatrix}$$ calcolata per $\underline{u}=\underline{u}^{i}$.

Nella Figura (b) sono rappresentati i due piani tangenti $T_{1}^{i}(\underline{u})$ e $T_{2}^{i}(\underline{u})$ con curve di livello, che nel caso di piani sono sempre rettilinee,completamente note .

La linea di livello di valore $T_{1}^{i}(\underline{u})=0$, rappresenta il luogo dei punti tali per cui la forma linearizzata della funzione prima componente del residuo si annulla (cioè si annulla il piano tangente alla prima componente del residuo, nel punto $( \underline{u}^{i} , r_{1}(\underline{u}=\underline{u}^{i}) )$.

Si può dire lo stesso per la linea di livello di valore $T_{2}^{i}(\underline{u})=0$.

Siccome tali curve di livello sono rette, per trovare il punto di incontro delle due curve di valore zero sarà dunque sufficiente risolvere un sistema di due equazioni lineari in due incognite. Le incognite in questione non sono altro che le componenti di $\underline{u}^{i+1}$ punto del piano $(\underline{u}_{1} , \underline{u}_{2})$, punto di nuova iterazione.

Allo step successivo (i+1-esimo) si dovranno nuovamente individuare due piani, rispettivamente tangenti alle curve $r_{1}(\underline{u})$ ed $r_{1}(\underline{u})$, nella nuova configurazione $\underline{u}^{i+1}$ :

• $T_{1}^{i+1}(\underline{u})$ è tangente ad $r_{1}(\underline{u}=\underline{u}^{i+1})$
• $T_{2}^{i+1}(\underline{u})$ è tangente ad $r_{2}(\underline{u}=\underline{u}^{i+1})$

Si dovrà poi graficare tali piani secondo curve di livello (di forma rettilinea e completamente note) ed individuare il punto di incontro delle curve rettilinee a valore nullo. Sarà poi possibile procedere al calcolo di $\underline{u}^{i+2}$ mediante la risoluzione di un nuovo sistema lineare.

L’iterazione proseguirà, così come descritto, sino al raggiungimento dei criteri d’arresto inizialmente imposti.

Nel caso di figura si noti come la configurazione $\underline{u}^{i+1}$ sia più vicina della $\underline{u}^{i}$ alla soluzione $\underline{u}^{*}$, sintomo del fatto che il metodo sta convergendo al risultato cercato. Non è tuttavia possibile conoscere a priori se il metodo convergerà o meno alla soluzione.

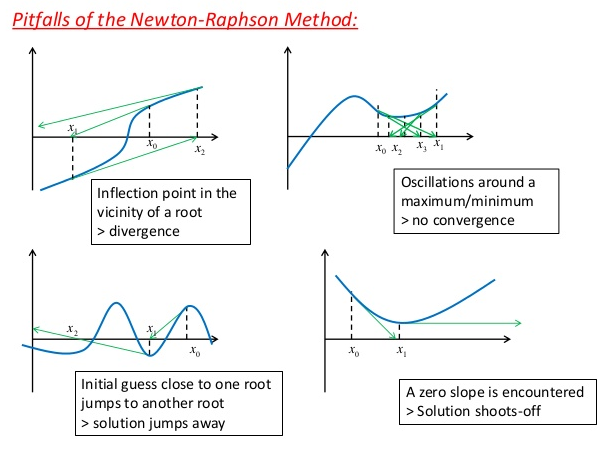
Nel caso monodimensionale il metodo può non risultare convergente per diverse motivazioni di semplice rappresentazione:

Si noti per esempio il caso, citato anche in aula, in cui nell’iterazione si incontra un punto della funzione a tangente orizzontale. L’estensione bidimensionale di questa condizione è rappresentata da una matrice Jacobiana completamente nulla, in uno dei punti di campionamento.

In realtà il metodo per il caso 2D non converge anche quando la matrice Jacobiana è singolare nel punto di campionamento. In questo caso esiste una retta appartenente ad uno dei piani tangenti che è parallela al piano $u_{1}u_{2}$ ( e che quindi non lo interseca mai ). Muovendosi quindi lungo la direzione individuata da tale retta la si ha quindi una componente del residuo che non cambia (non cambiano le reazioni elastiche oppure la variazione delle reazioni elastiche è completamente compensata dalla variazione delle forze esterne, funzione della configurazione. In altri termini si presenta una condizione di equilibrio indifferente).

Come si è potuto notare, il caso 2D è di non semplice rappresentazione, tuttavia è stato portato come esempio poiché rappresentativo dei casi più generali N-Dimensionali. In particolar modo il caso monodimensionale è di grande chiarezza grafica e didatticamente utile per comprendere il metodo, tuttavia l’insieme $\mathbb{R}$ è un insieme ordinato mentre $\mathbb{R}^{2}$ e di $\mathbb{R}^{n}$ che non sono propriamente ordinabili.