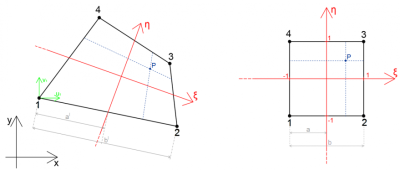
Per ogni punto di coordinate ξ,η possiamo ricavare l’associato punto in coordinate x,y semplicemente definendo le 4 funzioni di forma: $$N_{1,2,3,4} = \frac{\left ( 1\pm \xi \right )\left ( 1\pm \eta \right )}{4}$$ il legame diventa: $$\left\{\begin{matrix} x(\xi, \eta ) =\sum_{i}^{4}N_{i}(\xi, \eta )x_{i}\qquad(1)\\ y(\xi, \eta ) =\sum_{i}^{4}N_{i}(\xi, \eta )y_{i} \end{matrix}\right.$$ Allo stesso modo, utilizzando le stesse funzioni di forma, è possibile definire gli spostamenti: $$U\left ( \xi ,\eta \right )=\sum_{i=1}^{4} N_{i}\left ( \xi ,\eta \right )U_{I}\qquad(2)$$

Si vogliano, ora, calcolare $\varepsilon _{x},\varepsilon _{y}, \gamma _{xy}$ partendo dagli spostamenti interpolati: $$\varepsilon _{x}= \frac{\partial u}{\partial x}$$ $$\varepsilon _{y}= \frac{\partial v}{\partial y}$$ $$\gamma _{xy}= \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}$$ In forma matriciale: $$\underline{\varepsilon }=\begin{bmatrix} \varepsilon _{x}\\ \varepsilon _{y}\\ \varepsilon _{xy} \end{bmatrix} =\begin{bmatrix} 1 &0 &0 &0 \\ 0&0 &0 &1 \\ 0 &1 &1 &0 \end{bmatrix} \begin{bmatrix} \frac{\delta u}{\delta x}\\ \frac{\delta u}{\delta y}\\ \frac{\delta v}{\delta x}\\ \frac{\delta v}{\delta y} \end{bmatrix}\qquad(3)$$ La matrice 3×4 nella (3) viene indicata come $\underline{H}$.

Calcolare queste derivate è complesso, è molto più semplice ricavare: $$\frac{\partial u}{\partial \xi }, \frac{\partial u}{\partial \eta }, \frac{\partial v}{\partial \xi }, \frac{\partial v}{\partial \eta }$$ Quest'ultime, infatti, sono legate alle derivate in ξ,η delle funzioni di forma e alle coordinate nodali: $$\begin{bmatrix} \frac{\delta u}{\delta \xi }\\ \frac{\delta u}{\delta \eta }\\ \frac{\delta v}{\delta \xi }\\ \frac{\delta v}{\delta \eta } \end{bmatrix} = \underline{Q}(\xi ,\eta) \begin{bmatrix} u_{1}\\ v_{1}\\ u_{2}\\ v_{2}\\ u_{3}\\ v_{3}\\ u_{4}\\ v_{4} \end{bmatrix}\qquad(4)$$ Avendo definito $\underline{Q}(\xi ,\eta )$ come: $$\underline{Q}(\xi ,\eta )= \begin{bmatrix} \frac{\delta N_{1}}{\delta \xi } &0 &\frac{\delta N_{2}}{\delta \xi } &0 &\frac{\delta N_{3}}{\delta \xi } &0 &\frac{\delta N_{4}}{\delta \xi } &0 \\ \frac{\delta N_{1}}{\delta \eta } &0 &\frac{\delta N_{2}}{\delta \eta } &0 &\frac{\delta N_{3}}{\delta \eta } &0 &\frac{\delta N_{4}}{\delta \eta } &0 \\ 0&\frac{\delta N_{1}}{\delta \xi }& 0 & \frac{\delta N_{2}}{\delta \xi } &0 &\frac{\delta N_{3}}{\delta \xi } &0 &\frac{\delta N_{4}}{\delta \xi } \\ 0& \frac{\delta N_{1}}{\delta \eta }& 0 & \frac{\delta N_{2}}{\delta \eta } &0 &\frac{\delta N_{3}}{\delta \eta } &0 &\frac{\delta N_{4}}{\delta \eta } \end{bmatrix}$$ Ed essendo: $$\underline{δ}= \begin{bmatrix} u_{1}\\ v_{1}\\ u_{2}\\ v_{2}\\ u_{3}\\ v_{3}\\ u_{4}\\ v_{4} \end{bmatrix}$$ il vettore degli spostamenti nodali (indipendenti da ξ,η).

Il legame tra le derivate di u e v, nei due sistemi di riferimento, era stato calcolato come: $$ \begin{bmatrix} \frac{\partial u}{\partial \xi} \\\frac{\partial u }{\partial \eta} \end{bmatrix} = \begin{bmatrix} \frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} \\\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial u}{\partial x} \\\frac{\partial u}{\partial y} \end{bmatrix} $$ $$ \begin{bmatrix} \frac{\partial v}{\partial \xi} \\\frac{\partial v }{\partial \eta} \end{bmatrix} = \begin{bmatrix} \frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} \\\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial v}{\partial x} \\\frac{\partial v}{\partial y} \end{bmatrix} $$ é possibile allora definire lo Jacobiano trasposto e condensare le due matrici in una sola: $$\left [ \underline{\underline{J}}^T \right ]^{-1}=\begin{bmatrix} \frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} \\\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} \end{bmatrix}$$ $$\begin{bmatrix} \frac{\delta u}{\delta x}\\ \frac{\delta u}{\delta y}\\ \frac{\delta v}{\delta x}\\ \frac{\delta v}{\delta y} \end{bmatrix} = \begin{bmatrix} \underline{J_{11}^{-1}} &\underline{J_{12}^{-1}} &0 &0 \\ \underline{J_{21}^{-1}} &\underline{J_{22}^{-1}} &0 &0 \\ 0& 0 & \underline{J_{11}^{-1}} &\underline{J_{12}^{-1}} \\ 0 & 0& \underline{J_{21}^{-1}} &\underline{J_{22}^{-1}} \end{bmatrix} \begin{bmatrix} \frac{\delta u}{\delta \xi}\\ \frac{\delta u}{\delta \eta}\\ \frac{\delta v}{\delta \xi}\\ \frac{\delta v}{\delta \eta} \end{bmatrix}\qquad(5)$$ La matrice 4×4 trovata nell'equazione (5) si indica con $J_{inv}^{*}$.

Possono essere descritte a questo punto le deformazioni nel sistema naturale:

$$\underline{\varepsilon }=\underline{H}\cdot \underline{J_{inv}^{*}}(\xi ,\eta )\cdot \underline{Q}(\xi ,\eta )\cdot \underline{\delta }\qquad(6)$$ In analogia a quanto fatto per il triangolare 3 nodi è possibile chiamare: $$\underline{H}\cdot \underline{J_{inv}^{*}}\cdot \underline{Q}=\underline{B}(\xi, \eta )\qquad(7)$$ e quindi definire la matrice rigidezza dell'elemento come: $$\underline{\underline{K}}=\iint_{a}\underline{\underline{B}}^T\left ( \xi ,\eta \right )\underline{\underline{D}} \underline{\underline{B}}\left ( \xi ,\eta \right )\partial a\qquad(8)$$ Il $\partial a$ è espresso in x,y ma non è comodo integrare in questo dominio, quindi è necessario effettuare un cambio di variabile, in modo da poter integrare in ξ,η.

Lo Jacobiano è calcolato attraverso le derivate di x,y in ξ,η, le quali x,y sono legate alle funzioni di forma attraverso la (1). Quindi, lo Jacobiano avrà dei termini lineari in ξ e dei termini lineari in η: $$J=\begin{bmatrix} a+b\eta & c+d\xi \\e+f\eta & g+h\xi \end{bmatrix}=\begin{bmatrix} A & C \\B & D \end{bmatrix}$$ $$\left [ \underline{\underline{J}}^T \right ]=\begin{bmatrix} A & B \\C & D \end{bmatrix}$$ $$\left [ \underline{\underline{J}}^T \right ]^{-1}=\frac{1}{AD-BC}\begin{bmatrix} D & -B \\-C & A \end{bmatrix}$$

A,B,C,D sono lineari in ξ,η ma nell'inversa dello Jacobiano trasposto compaiono anche al denominatore, quindi si ottiene una razionale fratta che non è più semplicemente lineare. Di conseguenza, finché l'ordine al denominatore è basso si ottengono formule esatte per l'integrazione ma, ad esempio, un 8 nodi non è più integrabile in forma esatta.

Si prenda un punto in ξ,η e lo si incrementi di un dξ e di un dη lungo le due direzioni fino ad ottenere il quadratino di area dξdη:

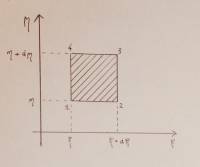
Questo quadratino viene trasformato nel piano x,y in questo modo:

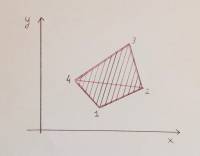
• il punto 1 è mappato in x(ξ,η) - y(ξ,η)
• il punto 2 è mappato in x(ξ+dξ,η) - y(ξ+dξ,η)
• il punto 3 è mappato in x(ξ+dξ,η+dη) - y(ξ+dξ,η+dη)
• il punto 4 è mappato in x(ξ,η+dη) - y(ξ,η+dη)

L'area dell'elemento in figura (3) è difficile da calcolare, è possibile, però, ottenere quest'ultima come somma delle aree di due triangoli che lo compongono (come rappresentato nella fig.3).

Pertanto, di seguito, è riportato il calcolo di questi sottoelementi.Valendo:

$$F\left ( \xi +d\xi ,\eta \right )\simeq F\left ( \xi ,\eta \right )+\frac{\partial F}{\partial \xi }|_{\xi ,\eta}d\xi $$ $$F\left ( \xi ,\eta +d\eta \right )\simeq F\left ( \xi ,\eta \right ) +\frac{\partial F}{\partial \eta }|_{\xi ,\eta}d\eta$$ $$F\left ( \xi +d\xi ,\eta +d\eta \right )\simeq F\left ( \xi ,\eta \right )+\frac{\partial F}{\partial \xi }|_{\xi ,\eta}d\xi +\frac{\partial F}{\partial \eta }|_{\xi ,\eta}d\eta$$ è possibile scrivere l'area del triangolo 124 come:

$$A_{124|(x,y)}=\frac{1}{2!}\begin{vmatrix} 1 & 1 &1 \\ x\left ( \xi ,\eta \right )& x(\xi ,\eta )+\frac{\partial x}{\partial \xi }d\xi & x(\xi ,\eta )+\frac{\partial x}{\partial \eta }d\eta \\ y\left ( \xi ,\eta \right ) & y(\xi ,\eta )+\frac{\partial y}{\partial \xi }d\xi& y(\xi ,\eta )+\frac{\partial y}{\partial \eta }d\eta \end{vmatrix}$$ Utilizzando una regola delle matrici per cui “la sottrazione di una riga per una combinazione di un'altra, non cambia il determinante” si ha: $$A_{124|(x,y)}=\frac{1}{2}\begin{vmatrix} 1 & 1 &1 \\ 0& \frac{\partial x}{\partial \xi }d\xi & \frac{\partial x}{\partial \eta }d\eta \\ 0 & \frac{\partial y}{\partial \xi }d\xi& \frac{\partial y}{\partial \eta }d\eta \end{vmatrix}$$

Sviluppando i calcoli: $$A_{124|(x,y)}=\frac{1}{2}\begin{bmatrix} \frac{dx}{d\xi} & \frac{dx}{d\eta}\\ \frac{dy}{d\xi} & \frac{dy}{d\eta} \end{bmatrix} d\xi d\eta = \frac{1}{2}\left | J \right | d\xi d\eta$$

Occorre notare che il determinante all'interno della formula presentata non è altro che il determinante della matrice Jacobiana, lo Jacobiano e le derivate in esso presenti sono valutate nello specifico $ξ$ ed $η$, essendo sviluppi nell’intorno del punto generico.

Inoltre il triangolo identificato nel piano ($x$,$y$) è la trasposizione sul piano fisico di quello presente sul piano ($ξ$,$η$): l’area $A_{124}$ è propria del triangolo sul piano naturale trasformato in quello fisico, mentre l’area del medesimo triangolo sul piano fisico ($ξ$,$η$) era

$$A_{124|(\xi,\eta)}= \frac{1}{2} d\xi d\eta $$

Questo vuol dire che il legame fra l’area del triangolo nel piano fisico e quello naturale è semplicemente il determinante della Jacobiana: infatti quest’ultimo è quel fattore che scala l’area sul piano naturale per ottenere quella sul piano fisico.

Svolgendo i medesimi passaggi per il triangolo 234, si trova un’identica relazione:

$$A_{234|(x,y)}=\frac{1}{2}\begin{bmatrix} \frac{dx}{d\xi} & \frac{dx}{d\eta}\\ \frac{dy}{d\xi} & \frac{dy}{d\eta} \end{bmatrix} d\xi d\eta = \frac{1}{2}\left | J \right | d\xi d\eta$$

Allora lo Jacobiano è il fattore che trasforma $A_{124}$ sul piano naturale in quella del triangolo 124 sul piano fisico ed anche $A_{234}$ appartenente al piano naturale a quella nel piano fisico. A questo punto si ha che:

$$dA_{(x,y)}=|J| dA_{(\xi,\eta)}$$

Allora la Matrice di Rigidezza dell’elemento sarà:

$$\underline{K}=\int_{-1}^{1}\int_{-1}^{1}\underline{B}^T(\xi,\eta)\ \underline{D}\ \underline{B}(\xi,\eta)\left | J \right |_{(\xi,\eta)}d\xi d\eta$$