Exam like exercises
MSC.Marc/Mentat
pierced tubolar profile
steel, thickness 0.5 mm
four basic loadcases
- axial load, 15.708 N
- x-oriented bending moment, 37.493 Nmm
- y-oriented bending moment, 37.493 Nmm
- torsional moment, 74.987 Nmm
the magnitude of the resultants are defined in order to obtain unit axial or shear stress values on the unnotched part.
For each loadcase, evaluate the peak equivalent von Mises stress along the structure.
You may resort to RBE2 links at beam ends; the slave nodes may be constrained in their full set of d.o.f.s .
The proposed modeling should take advantage of problem symmetries or skew-symmetries, if any. Please pay attention in suitably removing residual rigid body motions.
Further loadcases may be defined based on the evaluation of the bending and torsional stiffnesses for the meshed component.
In the case of bending, the buckling load may be further determined by resorting to the Linearized Pre-Buckling analysis procedure (
Buckle loadcase).
Maxima
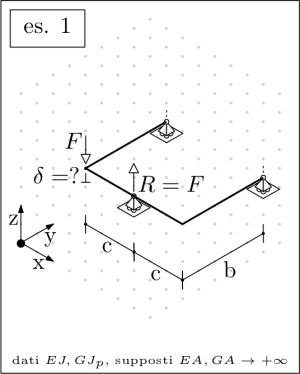
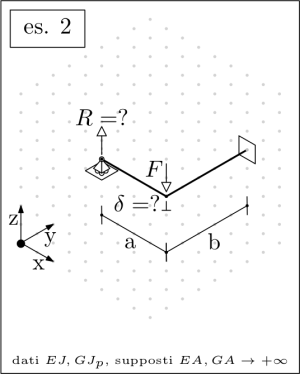
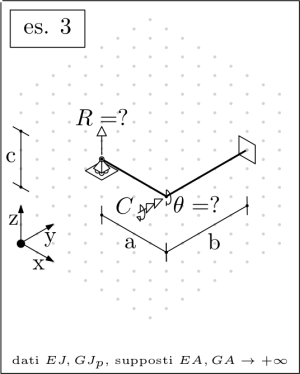
Consider the following structures and write a maxima worksheet that returns in a parametric form the requested deflections, rotations, reaction forces or reaction moments.
A hollow circular cross section is assumed, for which all the centroidal directions are principal of inertia, and share a common moment of inertia J; the shear center is positioned in correspondence to the centroid. See below for the actual sizing.
| exercise | solution |
|---|---|
 | maximaMSC.Marc control model |
 | maxima MSC.Marc control model |
 | maxima MSC.Marc control model |
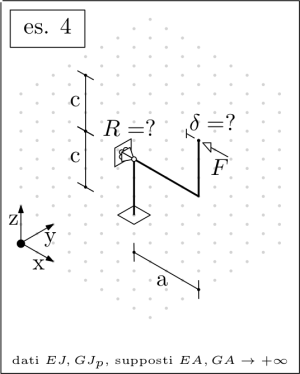 | maxima MSC.Marc control model -  Despite the appearances, the hinge at the support is external with respect to the beam; the latter is continuous and it is not split by the hinge itself Despite the appearances, the hinge at the support is external with respect to the beam; the latter is continuous and it is not split by the hinge itself |
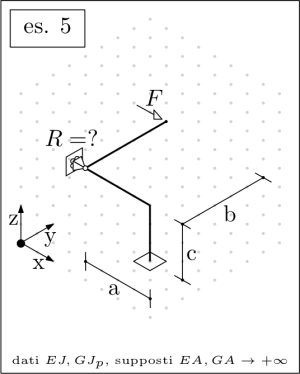 | MSC.Marc control model -  Despite the appearances, the hinge at the support is external with respect to the beam; the latter is continuous and it is not split by the hinge itself Despite the appearances, the hinge at the support is external with respect to the beam; the latter is continuous and it is not split by the hinge itself |
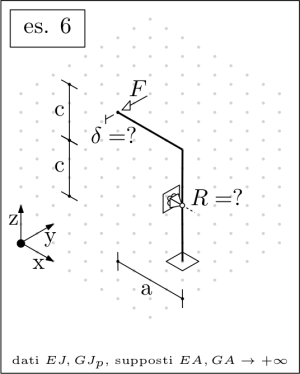 |  Despite the appearances, the hinge at the support is external with respect to the beam; the latter is continuous and it is not split by the hinge itself Despite the appearances, the hinge at the support is external with respect to the beam; the latter is continuous and it is not split by the hinge itself |
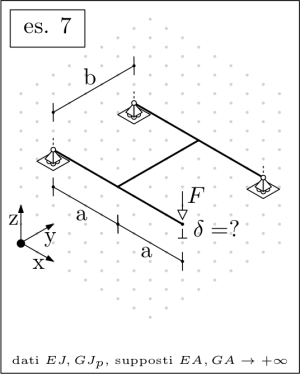 | maxima static equilibrium analysis |
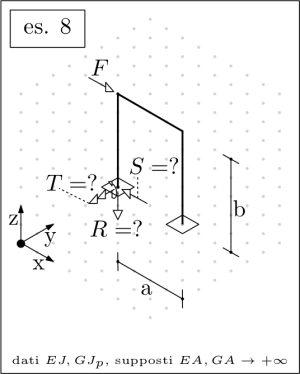 | maxima |
 | Bending and torsional moment diagrams maxima MSC.Marc control model |
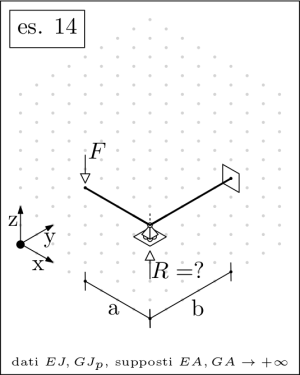 | Bending and torsional moment diagrams maxima MSC.Marc control model |
Finally, the unknown may be numerically evaluated according to the following sizing:
dim: [a=800,b=1000,c=600,F=1000,C=500000, E=210000,G=210000/2/(1+3/10), J=(40^4-36^4)*%pi/64,Jp=(40^4-36^4)*%pi/32];
The second Castigliano Theorem may be employed in evaluating rotations and deflections, and the overall strain energy may be defined based on the torsional and bending moments contributions alone. The axial load and the shear force contributions to the strain energy is to be assumed negligible.
If needed, the reaction forces of a statically determinate structure may be defined by casting and solving in Maxima a suitable set of equilibrium equations.
In the case multiple loads (external loads or parametrically defined constraint reactions) are applied to the structure, it is suggested to define bending and torsional moment diagrams separately for each load, and then resorting to superposition in obtaining cumulative diagrams.
MSC.Marc may be employed in indipendently obtaining the unknown results. See e.g. exercises 13-14.
In MSC.Marc, request the following outputs from the JOB RESULTS menu:
Beam Orientation Vector;Beam Bending Moment Local X;Beam Bending Moment Local Y;Beam Torsional Moment;
those quantities may be observed by resorting to the BEAM DIAGRAM section of the second page of the POSTPROCESSING RESULTS menu.
Diagrams may be scaled up to the requires size through the associated SETTINGS menu.
