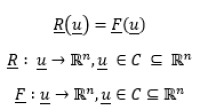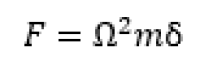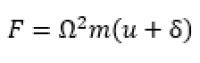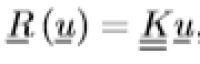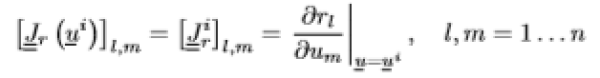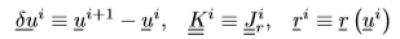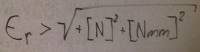Lezione a cura di Francesco Ronzini —> da ricontrollare
Algoritmo Newton-Raphson per sistemi di equazioni non-lineari
Considero un sistema non lineare di n equazioni
Si ha un'eguaglianza di funzioni vettori di variabile vettore. Nel caso specifico della soluzione di sistemi di equazioni derivate dagli equilibri nodali di strutture discretizzate con metodo FEM ho che questi oggetti hanno significati specifici.
In particolare u è un vettore che contiene le componenti di spostamento e rotazione nodale rispetto ad una configurazione dichiarata indeformata, lo spostamento rispetto all’indeformata è la nostra incognita. F è un termine noto in funzione delle variabili quindi è un’incognita anch’esso, è un vettore contenente le componenti di forza e coppia nodale applicata dall’esterno sul sistema, supposte note per una data configurazione della struttura. Cioè noto u riesco a ricavare le forze.
Perché si vogliono utilizzare queste forze in funzione delle configurazioni? Perché esistono in meccanica alcuni casi specifici di forze che sono funzione della posizione del nodo in cui sono applicati, gli esempi tipici sono :
1. Forza centrifuga
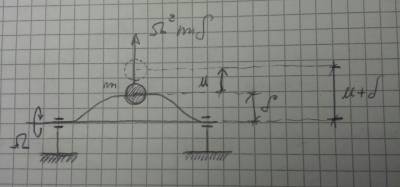
Si ha un motore che potrebbe avere il suo specifico problema di instabilità. Questo rotore in configurazione deformata nasce storto poiché c’è un errore geometrico nella costruzione dell’albero, quindi fisicamente il rotore è storto. Per semplicità lo considero privo di massa e tutta la massa la considero concentrata in un punto. Questo punto materiale è spostato rispetto all’asse di una quantità pari a δ. Avviene la rotazione che induce al punto una forza centrifuga. Se la rotazione è di entità Ω
questa è l’entità ella forza nell’intorno della configurazione indeformata. Ovviamente può succedere che a fronte dell’applicazione di questa forza questa massa si posti ulteriormente in direzione radiale, per cui la sua posizione diventa, se questo è lo spostamento u. un u+δ
Perciò la forza esterna diventa però u è la posizione incognita. In questo caso le forze esterne sono funzione della posizione dei nodi.
2. Trave che flette
Si prenda una trave incastrata e la si carichi con un razzetto in testa, che spinge con spinta da razzo. Il punto sul quale è applicata questa spinta è saldato in testa alla trave. Quando la trave è verticale, la forza che imprime alla stessa è verticale. Se la trave si deforma, in particolare flette, il nostro razzetto applica una spinta che è sempre comunque allineata con la tangente al terminale della trave. Questo tipo di forze nei codici vengono chiamate following forces, cioè le forze che “seguono” la deformata.
Abbiamo giustificato il perché aprirci alla possibilità di una forza esterna che è funzione della deformata. Tornando al sistema iniziale R è un vettore, definisce la risposta elastica non lineare della struttura. In pratica è un vettore che contiene le componenti azioni nodali necessarie a mantenere una struttura in equilibrio nello stato deformativo associato al vettore spostamento nodale u, ovvero quel vettore contente le componenti delle azioni nodali associate (in particolare uguali e contrarie) alle reazioni elastiche della struttura costrette in trave in stato deformata. Cioè se si applica ad ogni nodo un vincolo che lo costringe a stare in una configurazione deformata, le reazioni vincolari che si ottengono su quei vincoli si prendono e si cambiano di segno. Nel caso particolare di un sistema elastico lineare, R(u) non è altro che la matrice di rigidezza per u stesso, lo si può anche scrivere in forma diversa, senza perdere di generalità, come
Il fatto di aprire alla possibilità che la matrice K dipenda da u induce non linearità. F, i carichi esterni, possono essere anche funzioni dell’entità degli spostamenti imposti, si risolva il problema dicendo che sistema di partenza è già vincolato. Quindi quello che si chiama F in realtà è già F_constrain. Fc in vincolo è già stato inserito nel termine noto. Quell’oggetto è funzione delle forze applicate ma anche dei vincoli. Il concetto è che sistema non è ulteriormente da vincolare. I gradi di libertà sono già quelli indipendenti.
Una scrittura alternativa prevede la definizione e poi l'annullamento di un termine di resisduo. In particolare definisco come Residuo (r), cioè R - F, il sistema di equazioni che lo rendo in forma di residuo uguale a zero.
In questo modo riesco a rendere queste due funzioni non lineari e ad indurla ad un unico oggetto per semplicità. Le ho tenute separate perché ognuna delle due ha un significato ben precisa nel caso strutturale. Le azioni esterne e le reazioni elastiche del sistema.
Il metodo di Newton è unidimensionale. Si può usare il metodo di bisezione per poter risolvere il caso di un’equazione non lineare, non è pensabile di applicare il metodo di bisezione ad un sistema di equazioni di n incognite, si può ancora fare ma non tutto quello che funziona in 2D può essere espanso all’ “enne-D”. Comunque il metodo di N-R è costituito partendo dallo sviluppo in serie di Taylor al primo ordine dell’equazione di equilibrio, nell’intorno di un a configurazione. È un metodo iterativo, in ogni caso propongo una configurazione deformata e cerco una configurazione deformata migliore. Questo è il senso di uno step. Questo step mi dovrebbe fornire una configurazione con residuo minore, una in cui il disequilibrio è calato. Suppongo di avere una proposta che la mia i-esima proposta di iterato nella configurazione deformata. Un sistema non-lineare non si sa come trattarlo se prima non lo si linearizza. Di fatto si linearizza il sistema di equazioni nell’intorno della mia proposta i-esima per la deformata. Posso scrivere un’espressione in serie di Taylor multivariata, sviluppo non è solo per una variabile, c’è un blocco di derivate parziali, ecco perché è presente lo Jacobiano. Espando e chiamo U_star la soluzione esatta, che non conosco. Il residuo di U_star può essere scritto come il residuo calcolato sulla mia proposta di configurazione deformata più un termine correttivo al primo ordine che è definito dallo Jacobiano.
J_ r è una matrice i cui termini alla riga l e colonna m sono definibili da derivate parziali dell’ellesima componente del residuo rispetto alla componente dell’ emmessimo componente della variabile indipendente u. Questa derivata viene calcolata nella mia configurazione proposta.
Se si vuole avvicinare questa scrittura a quell’espansione in serie di Taylor monodimensionale bisogna agire in tale modo
Questo vettore è fatto di componenti, si prenda la sua ellesima componente di questo U_star che risulta essere pari all’ellesima componente del residuo calcolato nel punto nell’intorno del quale opero la linearizzazione. Quest’oggetto oggetto è un set residuo in corrispondenza della soluzione esatta del residuo stesso.
Lo Jacobiano del residuo è definito come differenza dei due Jacobiani essendo la sottrazione un’operazione lineare.
Dall’espansione di Taylor scritta prima, trascurando il termine di ordine superiore, tale identità, scrittoa per ogni variabile in forma vettore, non risulterà più strettamente verificata. Invece di scaricare l’errore in quell’o_piccolo lo si scarica tutto trasformando quell’U_star in u che non è più quello esatto ma un meno pretensioso termine di iterato successivo. In definitiva se si toglie quell’o piccolo l’equazione non vale più, ma invece di gestire l’errore non pretendendo più che in quel punto ci sia soluzione esatta (ci metto dentro un’altra entità vettoriale che riuscirà assestandosi a compensare il disequilibrio), quel vettore lo si inserirà nella trattazione come iterato successivo. Quindi prendendo spunto dall'espensione in sviluppo di Taylor multivariarta e scartando l'o_piccolo, ed errore lo si sposta, passando da un U_star esatto ad U_star diverso che non sarà soluzione esatta come caso precedente ma che si pretende che si avvicini in maniera sostanziale. Facendo così mi aspetto un errore che sia superiore ad un infinitesimo di ordine superiore rsipsteoo a soluzione con U_star.
Ispirandosi a questa formula con cambiamenti che si sono definiti, si riesce ad arrivare a tale forma, per cui lo Jacobiano calcolato con configurazione deformata, si può compattare la notazione semplicemente con Jacobiano i-esimo. Lo Jacobiano della funzione residuo calcolato nella configurazione proposta i-esima, moltiplicato per quest’oggetto incognito, moltiplicato per lo scostamento che mi porta dalla configurazione attuale a quella successiva di iterato, è uguale meno il residuo nella configurazione attuale. Quest’oggetto mi definisce un sistema di equazioni lineari, che supposto che lo Jacobiano non sia singolare, dà soluzione, e tale soluzione è nella forma di questo vettore, differenza tra iterato successivo ed iterato iniziale.
Risolvo un sistema lineare ed assegno soluzione al vettore delle incognite. Quindi quest’oggetto è la soluzione di un sistema lineare di equazione che ha residuo dell’iterato corrente come termine noto e lo Jacobiano all’iterato corrente come matrice di sistema, quest’oggetto è vettore soluzione. L’iterato i+1 è il nuovo iterato attuale – l'iterato che mi fornisce la soluzione al caso precedente. Ad ogni iterato devo risolvere un sistema che ha lo stesso numero di incognite e di equazioni del mio sistema lineare elastico equivalente. Quando approccio un calcolo non lineare di tipo strutturale, so immediatamente che costo computazionale sarà quello dell’equivalente sistema lineare ripetuto per ogni iterato N-R che mi serve per ravvicinarmi alle soluzioni. Non si sa a priori quanti siano gli iterati di N_R, dipende se convergono e con quale velocità ciò accade.
Da questa forma riesco a trovare un’analogia abbastanza evidente con il caso lineare, poiché questa è la linearizzazione del caso non lineare. Una volta definito il singolo iterato, avendo u_i posso ricavare u_i+1 a partire da U_i, mi basta fornire un vettore di primo tentativo U_0 che tipicamente per un caso strutturale è:
- se considero solo uno stato finale di carichi applicati parto dalla condizione di scarico e quindi avrò U_=0, questo potrebbe mettere in difficoltà il risolutore del metodo N-R poiché gli faccio eseguire un salto troppo elevato da scarico a caricato;
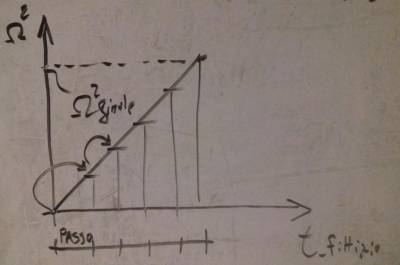
- definisco un a storia di carico definita per passi, al tempo zero ho un carico zero ed al tempo 1 ho il carico finale, definendo 20 intervalli intermedi, da un passo all’altro aggiungo solo un ventesimo di carico, aggiungo sempre come primo iterato da cui partire, quindi U_0, la deformata assunta dal mio sistema al livello di carico precedente. Se ho sistema per cui carico finale è di una certa entità non mi conviene di fare un salto in cui prendo la configurazione nulla come U_0 sperando che N- R mi dia risultato ad un caso finito, ma definisco una fittizia dimensione temporale. Nel caso del rotore (visto in precedenza) faccio variare Ω, se si vuole risolvere il problema conviene definire una modulazione di Ω tra valore nullo ad uno finale (per esempio Ω_finale^2). Definisco tanti step intermedi ed eseguo iterazione di N-R, utilizzando la condizione di scarico per cercare la soluzione ad un livello di carico parzializzato. Una volta trovata la soluzione utilizzo questa come inizio del metodo di N-R e così via.
Man mano che aumento livelli di carico io parto a cercare soluzione di carico incrementato con deformate associate ad un carico di base, che di fatto è sempre più vicino a quello incrementato, man mano che aumento il numero degli steps. Per cui di fatto passo a N-R ad ogni step di soluzioni deformative che sono più vicine a quelle finali, quindi lo aiuto a convergere. Devo anche definire un criterio di convergenza, in realtà né ho 2 di base.
1.1. Convergenza RESIDUI: fermo l’iterazione quando residuo associato all’iterato appena calcolato è minore di una certa soglia in norma e quella è una soglia assoluta. In che unità di misura verrà espresso?
in quella scrittura non c’è vero senso fisico soprattutto se le unità di misura sono associati a spostamenti misti, ovvero traslazioni e rotazioni. Ci potrebbero essere dei problemi quando gli spostamenti sono della scala dei mm, mentre le rotazioni sono in radianti, si potrebbero sommare oggetti con unità di misura diverse tra loro. Un termine però è generalmente più preponderante dell’atro. Questo comunque potrebbe dare problemi per la determinazione di una soglia di convergenza.
1.2. Convergenza alle INCOGNITE (nel caso FEM è una convergenza agli spostamenti) mi fermo quando iterato successivo è molto simile all’iterato che ho ottenuto in partenza, ovvero le variazioni che ottengo procedendo le iterazioni sono troppo piccole. Anche qui c’è un mix tra mm e radianti che dev’essere al di sotto di una certa soglia. Punto 1.1. e 1.2. riguardano procedure assolute.
2. Implementazione di livelli di tolleranza relativi, ovvero io vorrei che iterato procedesse finché la soluzione proposta di scosta da quella in cui sono partito meno dell’un per mille. Bisogna individuare opportuni termini di riferimento, in valore assoluto, per forze e spostamenti. La determinazione di questi termini di riferimento è abbastanza fattibile per gli spostamenti. Non esiste una modalità univoca per definire un termine di riferimento. Per le forze è un po’ un problema. Di solito quello che fa Marc usa il valore in modulo della massima reazione vincolare, il problema che il valore modulare di massima reazione vincolare per sistema auto-equilibrante è zero e quindi mi fermo quando raggiungo convergenza dell’1 per mille di zero, quindi non mi fermo mai. Il vero problema è definire i valori di rifermento. Sono aumentati anche i tempi di calcolo. Una possibile implementazione di quest’algoritmo è ciclo while riportato nella wiki.
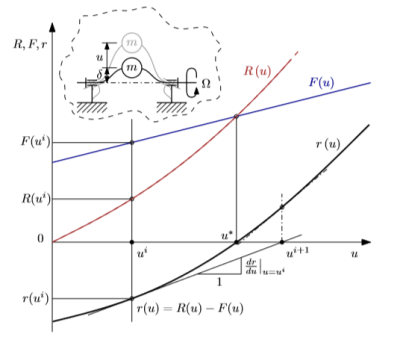
Graficamente nell’1D posso rappresentare il metodo di Newton come in dispensa wiki, ho che la forza esterna cresce linearmente con lo spostamento in questo caso centrifugo della massa, per via di quell’iniziale delta ho una forza non nulla anche in corrispondenza di scostamento nullo. Se albero fosse perfettamente rettilinea linea blu partirebbe proprio Da zero ma a causa di delta parte da un valore finito. Man mano che aumento spostamento centrifugo della mia massa che è l’unico valore incognito del mio problema, la forza esterna cresce. La reazione elastica cresca, ho supposto che questo sistema sia caratterizzato da un comportamento stiffering, ovvero che si aumenti la rigidezza all’aumentare della deformazione. Questo è dovuto al fatto che per piccole deformate quell’albero tende a lavorare a flessione rotante per grandi deformazioni invece tende a lavorare con sforzi normali. C’è una tendenza ad incrementare più che linearmente il carico all’aumentare dello spostamento. All’inizio trave cede sotto flessione e alla fine a sforzo normale. La soluzione si ha quando i carichi esterni sono uguali ai carichi necessari per giustificare elasticamente lo spostamento. La differenza R – F è di questa soluzione residuo. Parto da una configurazione di iterato i-esimo, mi calcolo il residuo (questa curva la ottengo alla fine dei miei iterati, ciò che conosco passo dopo passo di questo metodo è il punto di iterazione e la sua tangente). In questo punto tangente, abbiamo residuo, lo jacobiano, la soluzione di sistema lineare che ha come matrice lo Jacobiano e come termine noto il residuo, si risolve in maniera grafica cercando intersezione tra questa tangente con l’asse U, così troviamo l’iterato successivo, finché non ci si avvicina alla soluzione.