Appunti della lezione
a cura di Ulisse, ELENA DI TROIA, Diomede, Nessuno e Icaro
Elementi finiti: domini e funzioni interpolanti
Si può generalizzare quanto visto finora aggiungendo ulteriori quattro nodi per ogni centro lato del quadrato elementare. Procedo a tal riguardo similmente a quanto fatto in precedenza, introducendo un coefficiente incognito
$ a_{ij} $ per ogni nodo, si dà luogo a un polinomio di ottavo grado che sfrutta ogni combinazione possibile dei coefficienti con i parametri $\xi$ e $\eta$, ovvero:
$$a_{00}\cdot1$$ $$a_{10}\cdot\xi$$ $$a_{01}\cdot\eta$$ $$a_{11}\cdot\xi\eta$$ $$a_{20}\cdot\xi^2$$ $$a_{02}\cdot\eta^2$$ $$a_{21}\cdot\xi^2\eta$$ $$a_{12}\cdot\xi\eta^2$$
Come prima, fissando una delle due coordinate si passa da un andamento genericamente cubico, come mostrato dai coefficienti di ordine maggiore, ad un andamento quadratico. Ne segue che, se si analizza l'andamento della funzione di forma $N_1(\xi,\eta)$, sui lati del quadrato elementare a 8 nodi si avranno delle parabole che partono dal valore unitario sul nodo 1 e si annullano sia a centro-lato che sul vertice, ovvero:
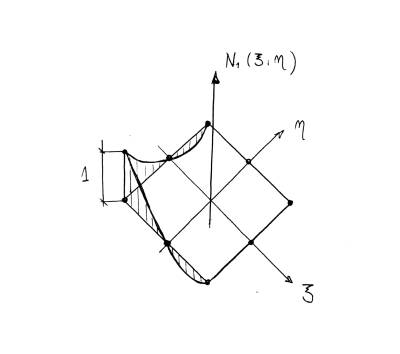
A titolo di esempio si riporta l'andamento anche di una funzione di peso riferita ad un nodo di centro-lato, per esempio $N_5(\xi,\eta)$:

Si può a questo punto generalizzare dicendo:
$$f(\xi,\eta)=\sum_{i=1}^{8} N_i(\xi,\eta)f_i$$
Si passi ora ad analizzare l'elemento triangolare a 3 nodi. Indifferentemente da prima, avremo tre coefficienti incogniti e tre equazioni, una per nodo, per cui tali coefficienti risultano determinati univocamente.
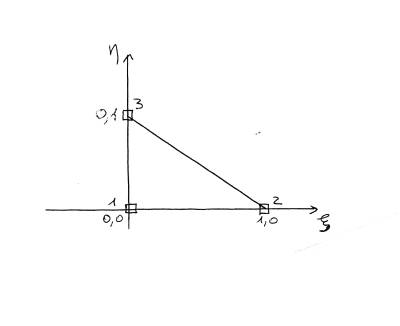 A titolo di esempio si riporta il sistema corrispondente alla funzione di forma $N_1(\xi,\eta)$, dove si sostituisce a $\xi$ e $\eta$ le coordinate di un nodo alla volta:
$$
\begin{cases}
a_{00}\cdot1+a_{10}\cdot0+a_{01}\cdot0=1\\
a_{00}\cdot1+a_{10}\cdot1+a_{01}\cdot0=0\\
a_{00}\cdot1+a_{10}\cdot0+a_{01}\cdot1=0
\end{cases}
$$
Risulta in questo caso che la derivata della funzione è una funzione lineare. Nel caso si implementino anche i punti intermedi, dando luogo all'elemento triangolare a 6 nodi, si ottiene un sistema di 6 equazioni in 6 incognite.
A titolo di esempio si riporta il sistema corrispondente alla funzione di forma $N_1(\xi,\eta)$, dove si sostituisce a $\xi$ e $\eta$ le coordinate di un nodo alla volta:
$$
\begin{cases}
a_{00}\cdot1+a_{10}\cdot0+a_{01}\cdot0=1\\
a_{00}\cdot1+a_{10}\cdot1+a_{01}\cdot0=0\\
a_{00}\cdot1+a_{10}\cdot0+a_{01}\cdot1=0
\end{cases}
$$
Risulta in questo caso che la derivata della funzione è una funzione lineare. Nel caso si implementino anche i punti intermedi, dando luogo all'elemento triangolare a 6 nodi, si ottiene un sistema di 6 equazioni in 6 incognite.
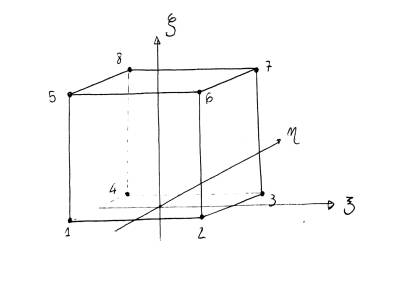
 Si estenda ora il ragionamento a elementi spaziali. Partendo dall'elemento cubico o esaedro a 8 nodi: si introduce il terzo asse, $\zeta$, e gli otto coefficienti $a_{ijk}$ da moltiplicare rispettivamente per le varie combinazioni di $\xi$, $\eta$, $\zeta$.
Si noti come, analogamente al caso bidimensionale, l'elemento finito cubico goda della proprietà di trilinearità, ovvero, fissando una delle tre coordinate, si ottengono andamenti parabolici.
Si estenda ora il ragionamento a elementi spaziali. Partendo dall'elemento cubico o esaedro a 8 nodi: si introduce il terzo asse, $\zeta$, e gli otto coefficienti $a_{ijk}$ da moltiplicare rispettivamente per le varie combinazioni di $\xi$, $\eta$, $\zeta$.
Si noti come, analogamente al caso bidimensionale, l'elemento finito cubico goda della proprietà di trilinearità, ovvero, fissando una delle tre coordinate, si ottengono andamenti parabolici.
Un ulteriore esempio: l'elemento tetraedrico a 10 nodi, 4 a vertice e 6 a centro spigolo (non lato). La particolarità di questo caso è quella di ottenere una forma quadratica completa, avendo rispettivamente 1, $\xi$, $\eta$, $\xi\eta$, $\eta\zeta$, $\xi\zeta$, $\xi^2$, $\eta^2$, $\zeta^2$ come termini da moltiplicare ai coefficienti.
Si traggano le conclusioni di quanto visto finora. Si deduce che, in presenza di nodi a centro-lato, le funzioni di forma sono almeno quadratiche, eventualmente qualcosa in più: nel caso del tetraedro e del triangolo sono perfettamente quadratiche, nel caso del quadrilatero e del cubo sono qualcosa in più. L'importanza di sapere l'andamento delle formule di interpolazione, se lineare, “più che lineare”, quadratico, “più che quadratico”, eccetera, (si ricorda che tali considerazioni sono relative alle funzioni di forma ma, essendo l'interpolazione una combinazione lineare delle funzioni di forma con i valori dei nodi, il ragionamento si estende anche alle formule di interpolazione) risiede nel fatto che , essendo le deformazioni definite come derivate degli spostamenti, un campo di deformazione lineare (per esempio) deriverà da un campo di spostamenti quadratici, e così via.
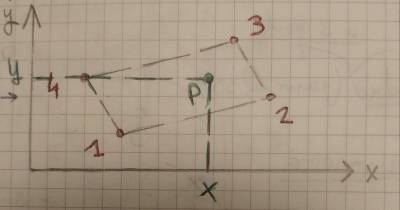
Tornando nel piano, si generalizza le considerazioni finora viste per un quadrato elementare ad un generico quadrilatero senza particolari proprietà di simmetria. Passo da un piano locale a un piano fisico $[x,y,z]$. Ogni nodo ha coordinate $x_i, y_i$, dove $i$ scorre da 1 a 4, il numero di vertici. A ognuno dei quattro nodi è inoltre associato un valore $f_i$.
L'obiettivo è ricavare una $f(x,y)$ per interpolare i dati dei quattro nodi ed arrivare al valore di $P(\xi,\eta)$. Ci si accorge che ciò è praticamente impossibile per la difficoltà nel ricavare le funzioni di forma: questo porta all'intuizione di usare i risultati ricavati per il quadrilatero elementare e di “tradurli” su un generico quadrilatero, creando al suo intero una mappatura.
Si definisce a questo punto una funzione che, dalle coordinate locali per un dato nodo, dia le corrispettive coordinate sul piano fisico: nel caso del nodo 1 si vuole quindi passare da $(\xi, \eta)=(-1,-1)$ a $(x,y)=(x_1,y_1)$. Si può quindi scrivere i seguenti risultati:
$$x(\xi,\eta)=\sum_{i=1}^{4}N_i(\xi,\eta)\cdot x_i$$ $$y(\xi,\eta)=\sum_{i=1}^{4}N_i(\xi,\eta)\cdot y_i$$
Si può calcolare il punto mediano del lato $12$, ma ci si accorge che tale punto è lo stesso anche per il quadrilatero sul piano fisico: questo perchè lungo un segmento la funzione è lineare, avendo una delle due coordinate fissata, e una funzione lineare restituisce sempre un segmento da un segmento. In pratica dunque l'asse $\xi$ passa per i due punti mediani di $12$ e $41$, quindi lo si può proiettare sul piano fisico; tali considerazioni valgono esattamente anche per l'asse $\eta$.
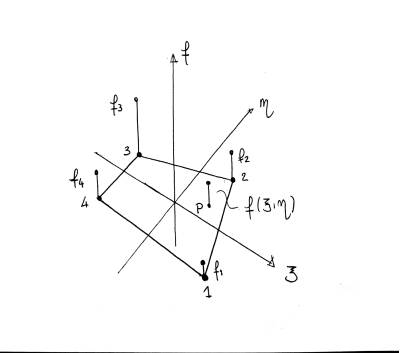
L'approccio pratico per ricavare la mappatura del generico quadrilatero e ricavare di conseguenza il valore del punto P sfruttando i quadrati elementari è il seguente: si misura l'inclinazione del primo lato, per esempio $12$, e di quello opposto, $34$, e progressivamente si inclinano i segmenti in modo che la transizione fra le due inclinazioni dei lati opposti risulti lineare. Una volta intercettato P in questa griglia si proietta verso il terzo asse una retta verticale. Per conoscere il valore di P su questa retta, sfruttando la linearità, si traccia un segmento fra i due punti dei lati $12$ e $34$ che giacciono sulla stessa riga disegnata in precedenza di P. Questo segmento collega i valori dei due punti (valori noti, essendo sul lato) lungo il terzo asse e di conseguenza un segmento lineare fra questi due punti permette di valutare anche il valore di P. Si riporta queste parole graficamente utilizzando la funzione di forma $N_2(\xi,\eta)$ a titolo esemplificativo:
Se $\xi$ o $\eta$ sono costanti, $x(\xi,\eta)$ e $y(\xi,\eta)$ sono funzioni lineari in $\xi$ e $\eta$. Salvo il caso limite in cui un lato collassi in un punto (caso comunque utilizzato nella pratica), x e y non sono mai costanti contemporaneamente, e vale, sui lati e su segmenti verticali e orizzontali: $$a\xi+b\eta+c$$ con $$a,b\neq0$$ ed è invertibile. Quindi, solo sui lati, posso ricavare la mappatura inversa: $$x(\xi,\eta)=\xi_{12}(x,y)$$ $$y(\xi,\eta)=\eta_{12}(x,y)$$ Come esempio, si prenda il lato $12$. Vale che: $$\eta=-1=cost.$$ $$f(\xi_{12}(x,y),\eta_{12}(x,y))$$ con $\xi_{12}(x,y)=x(\xi,\eta)$ e $\eta_{12}(x,y)=y(\xi,\eta)$
Si rileva nuovamente che l'interpolazione sui lati del quadrilatero generico, in accordo al quadrato elementare, è lineare.
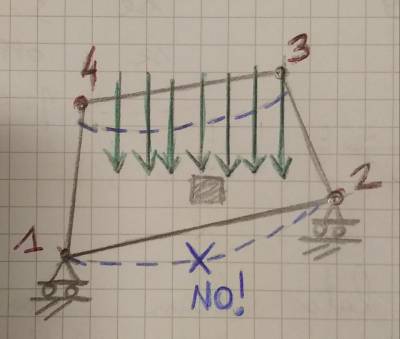
Le proprietà matematiche studiate finora non sono solo un puro esercizio ma sono indispensabili all'utilizzo responsabile dei software FEM. Sfogliando l'elenco degli elementi finiti sul software Marc/Mentat,infatti, si legge come per l'elemento quadrilatero generico l'interpolazione sia bilineare, come visto poc'anzi. Questa affermazione impone già determinati vincoli cinematici, se ne analizza uno:
Si analizza nell'immagine di cui sopra la deformata del quadrilatero, appoggiato sui vertici 1 e 2, sotto la forza peso. La deformata tracciata è puramente qualitativa ma permette di mettere in luce una deformazione che, seppure assolutamente realistica, viene inibita in questo particolare elemento finito, per come esso stesso è stato programmato. In particolare, essendo che $f=\sum_{i=1}^{4}N_i(\xi,\eta)*f_i$, dove f è una generica funzione, se alla f si sostituisce v, spostamento lungo y, risulta chiaramente che nessun punto lungo il lato $12$ può spostarsi, dal momento che i due vertici 1 e 2 sono vincolati e per questo motivo la sommatoria di questi due spostamenti nulla. In pratica, se immaginiamo che il quadrilatero sia fatto di gomma, si può pensare che il segmento $12$ sia fatto d'acciaio, o comunque di un materiale molto meno deformabile. Ne risulta che l'elemento quadrilatero risulta nativamente più rigido del corrispondente elemento nella realtà.
Si procede ora ad analizzare le derivate direzionali. Si ricorda la formula: $$N_i(\xi,\eta)=\dfrac{1}{4}(1\pm\xi)(1\pm\eta)$$ Risulta immediata la derivazione di tale formula in $\xi$: $$\dfrac{\partial N_1}{\partial \xi}=\dfrac{1}{4}(\eta-1)$$
Tuttavia questa derivata è poco interessante. I veri valori di interesse sono $\dfrac{\partial f}{\partial x}$ e $\dfrac{\partial f}{\partial y}$. Se al generico f sostituiamo lo spostamento lungo $x$, $u$, otteniamo due valori di effettiva concretezza fisica: $$\dfrac{\partial u}{\partial x}=\overline{\varepsilon}_x$$ e $\dfrac{\partial u}{\partial y}$ è una delle due parti di $\overline{\gamma}_{xy}$.
$\dfrac{\partial u}{\partial x}$ è molto complesso da calcolare, mentre le quantità $\dfrac{\partial u}{\partial \xi}$ e $\dfrac{\partial u}{\partial \eta}$ sono decisamente più semplici da calcolare; si prova ad aggirare il problema. Da formule già viste in precedenza vale che:
$$ \begin{bmatrix} \dfrac{\partial u}{\partial \xi}\\ \dfrac{\partial u}{\partial \eta} \end{bmatrix} = \sum_{i=1}^{4}\begin{bmatrix} \dfrac{\partial N_i}{\partial \xi}\\ \dfrac{\partial N_i}{\partial \eta} \end{bmatrix} u_i $$
Si cambino a questo punto le variabili di derivazione: $$\dfrac{\partial u}{\partial \xi}=\dfrac{\partial u}{\partial x}\cdot\dfrac{\partial x}{\partial \xi}+\dfrac{\partial u}{\partial y}\cdot\dfrac{\partial y}{\partial \xi}$$ $$\dfrac{\partial u}{\partial \eta}=\dfrac{\partial u}{\partial x}\cdot\dfrac{\partial x}{\partial \eta}+\dfrac{\partial u}{\partial y}\cdot\dfrac{\partial y}{\partial \eta}$$
Se ne ricava un sistema matriciale:
$$ \begin{bmatrix} \dfrac{\partial u}{\partial \xi}\\ \dfrac{\partial u}{\partial \eta} \end{bmatrix} = \begin{bmatrix} \dfrac{\partial x}{\partial \xi} & \dfrac{\partial y}{\partial \xi} \\ \dfrac{\partial x}{\partial \eta}& \dfrac{\partial y}{\partial \eta} \end{bmatrix} \begin{bmatrix} \dfrac{\partial u}{\partial x} \\ \dfrac{\partial u}{\partial y} \end{bmatrix} $$
L'ultima matrice colonna (derivata parziale di u rispetto a x e a y) risulta difficile da calcolare, come detto prima: saranno le incognite del problema matriciale. Si noti che la matrice 2×2 centrale è una Jacobiana trasposta (la trasposizione risiede nel fatto che nella matrice di cui sopra il denominatore varia per colonne mentre nello Jacobiano varia per righe, e discorso analogo per il numeratore): sia chiamata $J^T(\xi,\eta)$. Supponendo che questa matrice non sia singolare sostituisco all'espressione di prima:
$$ \begin{bmatrix} \dfrac{\partial u}{\partial x} \\ \dfrac{\partial u}{\partial y} \end{bmatrix} = (\underline{\underline{J}}^T)^{-1} \begin{bmatrix} \dfrac{\partial u}{\partial \xi} \\ \dfrac{\partial u}{\partial \eta} \end{bmatrix} $$
Per scrivere infine:
$$ \begin{bmatrix} \dfrac{\partial u}{\partial x} \\ \dfrac{\partial u}{\partial y} \end{bmatrix} = (\underline{\underline{J}}^T)^{-1} \begin{bmatrix} \dots & \dots & \dfrac{\partial N_i}{\partial \xi} & \dots & \dots\\ \dots & \dots & \dots & \dots & \dots\\ \dots & \dots & \dfrac{\partial N_i}{\partial \eta} & \dots & \dots \end{bmatrix} \begin{bmatrix} \dots\\ \dots \\ u_i \\ \dots \\ \dots \\ \end{bmatrix} $$
Come ultime considerazioni si riportano le seguenti: Lo Jacobiano è sì funzione delle coordinate nodali ma non è funzione di u, stesso discorso vale per la matrice subito successiva (quella con le funzioni peso), anch'essa non dipende da u. Questo porta a valutare l'intero membro di destra come lineare rispetto ad u.
Sezione a cura del docente
blablabla