Appunti della lezione
a cura di Andrea Di Lorenzo
CONTINUAZIONE STUDIO TAGLIO
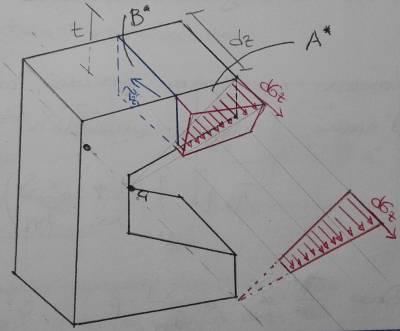
Si prenda una sezione generica. A questa si effettui un taglio retto. Isolando il concio della sezione, questo sarà caricato frontalmente da una $ d \sigma_z $. Se il materiale è uniforme, la tensione in considerazione è lineare lungo la sezione ($ \epsilon_z $ è lineare, $ E = cost $ perché il materiale è uniforme –> $ d \sigma_z $ lineare), con valore nullo nel luogo dei punti baricentrici.
[NB: Non è detto che l’asse baricentrico coincide con l’asse neutro. Coincidono i due solamente se il rapporto tra due momenti flettenti agenti su due piani differenti coincide con il rapporto tra i rispettivi tagli. Nella figura superiore asse baricentrico e neutro coincidono; in quella inferiore no.]
Integrando i contributi delle $ d \sigma_z $ sulla faccia $ A* $, questi devono essere equilibrati dalle azioni taglianti $ \tau_{zi} $ sulla faccia $ B* $ (faccia sulla quale è stato effettuato il taglio). Di queste azioni taglianti si considera comunque il loro valore medio lungo tutta la sezione. Questo perché si ha a disposizione una sola funzione da cui ottenere una sola incognita (τ medio appunto), una volta nota $ d \sigma_z $ e $ t $ (lunghezza del taglio, non per forza rettilineo). $$ \bar{\tau} t = \iint_{a*} \frac{\partial \sigma _{z}}{\partial z} da $$ Lavorando in sezioni particolari, con sistemi di riferimento baricentrici principali d’inerzia, l’integrale appena scritto si potrà ridurre solamente a $$ \bar{\tau_{zi}} t = \iint_{a*} ( \frac{yS_{y}}{J_{xx}} + \frac{xS_{x}}{J_{yy}} ) da = \frac{\bar{y*}A*}{J_{xx}}S_{y} + \frac{\bar{x*}A*}{J_{yy}}S_{x} $$
Con $ \bar{y*}A* $ e $ \bar{x*}A* $ rappresentanti i momenti del primo ordine, mentre $ J_{xx} $ e $ J_{yy} $ i momenti del secondo ordine. In poche parole, in queste particolari condizioni, ci troviamo nel caso della teoria di Jourawsky.
Sezione sottile aperta a C
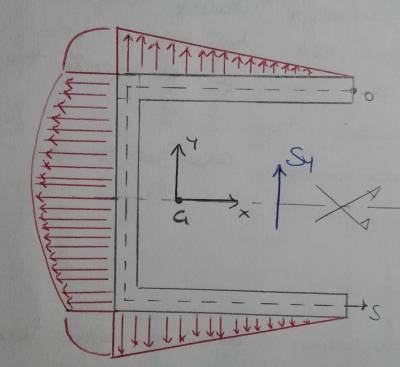
Si studi ora $ \bar{\tau_{zi}} t $ nelle condizioni semplificate (sistema di riferimento baricentrico con assi principali d’inerzia) così da poter utilizzare la formula nella sua versione più semplice. La sezione è simmetrica rispetto l’asse $ x $. Si consideri per ora la sezione soggetta al solo taglio $ S_{y} $ $$ \bar{\tau_{zi}} t = \frac{\bar{y*}A*}{J_{xx}}S_{y} $$ Definita l’ascissa curvilinea che attraversa l’asse medio della sezione:
- Per $ s = 0 $ –> $ \bar{\tau} = 0 $ . Questo è vero considerando la continuità delle tensioni, necessarie sulla superficie libera per avere una $ \bar{\tau} \neq 0 $. Inoltre $ A* = 0 $ .
- Si procede poi con tagli ortogonali alla sezione esterna (perché rappresenta il taglio più semplice da effettuare considerando che le $ \bar{\tau} $ devono essere parallele rispetto alla superficie libera). Man mano che ci spostiamo verso $ s $ crescente, il baricentro del concio $ G* $ (di coordinate $ \bar{x*}, \bar{y*} $ ) ha $ \bar{y*} $ costante lungo tutto il tratto orizzontale. L’area diversamente aumenta in maniera lineare. Nel complesso allora si avrà $ \bar{\tau} $ crescere linearmente con $ s $.
- Arrivati allo spigolo si ha continuità, in quanto calcolando i momenti del primo ordine subito prima e subito dopo questo, i tagli (al netto di errori infinitesimi) coincidono.
- Lungo il tratto verticale, $ \bar{y*} $ decresce linearmente e $ A* $ cresce linearmente. Complessivamente allora avrà $ \bar{\tau} $ crescere quadraticamente con una pendenza iniziale minore rispetto a quella su tratto orizzontale. Questo fino a $ s = \frac{L}{2} $ (considerando che l ascisse curvilinea vari tra 0 e L).
- Successivamente, per via della simmetria della struttura, il diagramma delle tensioni tangenziali è specchiato rispetto l’asse $ x $.
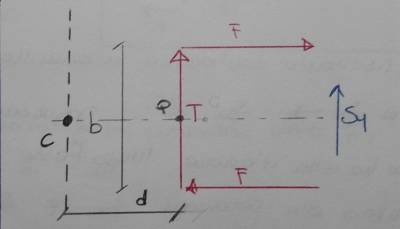
Finora non è stato assolutamente definito il centro di taglio. Considerando la risultante delle forze dovute alle tensioni tangenziali, sarà possibile calcolare una coordinata di questo. Per l’equilibrio, $ T \equiv S_{y} $ . Ricordando che il centro di taglio è il luogo dei punti lungo il quale, se applicati i tagli, i momenti torcenti si annullano, affinché ciò sia vero $$ S_{y} d = F b $$
Il punto $ C $ dovrà trovarsi su una verticale distante $ d $ dal punto $ P $. Così facendo il centro di taglio NON è univocamente definito. Sfruttando però la simmetria di questo, si potrà dire che il punto $ C $ deve trovarsi assolutamente dell’intersezione tra questo piano e al verticale trovata poco prima. Allora così facendo si può dire che il punto $ C $ è univocamente definito.
Non consideriamo ora la simmetria della struttura (così da metterci in un caso generico). Affinché il centro di taglio sia univocamente definito, bisogna fare lo stesso ragionamento fatto precedentemente con $ S_{y} $ , questa volta con $ S_{x} $.
Si prende sempre l’ascissa curvilinea s e al variare di questa si osserva:
- Per $ s=0 $ –> $ A*=0 $ –> $ \bar{\tau} = 0 $
- Per $ s $ crescente, $ A* $ aumenta e $ \bar{x*} $ decresce. L’andamento complessivo allora sarà parabolico, con massimo sulla verticale al baricentro.
- Come visto prima, lungo lo spigolo si ha continuità delle sollecitazioni
- Nel tratto verticale, la continua accumulazione dei contributi di $ \bar{x*} $ fa in modo che $ \bar{\tau} $ si annulli all’ altezza del baricentro. Il tutto con andamento lineare.
- Per simmetria si procede anche nella parte bassa della sezione.
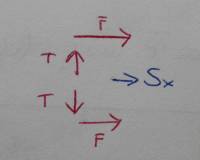
Si considerano le risultanti. I contributi sull’anima si elidono tra loro. Dall’equilibrio alle rotazioni di $ S_{x} $ con le due $ F $, fa capire come $ S_{x} = 2F $ e che deve trovarsi posizionato su un asse passante per l’asse $ x $ (coincidente nel caso con il piano di simmetria).
Intersecando questi due assi, questo appena ottenuto e quello ricavato dal procedimento con $ S_{y} $ si riesce a definire univocamente $ C $. Questo ragionamento è valido per qualsiasi sezione APERTA.
TAGLIO: SEZIONE SOTTILE CHIUSA
Questa volta, rispetto alla sezione aperta, non basterà effettuare un taglio nella sezione e spostare questo lungo $ s $ per vedere come variano le tensioni taglianti, ma bisognerà fare due tagli (per poter isolare un concio). Su entrambe le facce agiscono delle tensioni $ \bar{\tau}_{iz1} $ e $ \bar{\tau}_{iz2} $ le cui rispettive forze associate corrispondono a
$$ \bar{\tau}_{iz1} t_{1}dz = F_{1} $$ $$ \bar{\tau}_{iz2} t_{2}dz = F_{2} $$
Problema: si ha solo una funzione per il calcolo di $ \bar{\tau} $ (quella vista finora) per le due incognite. Bisognerà mettere l’una in funzione dell’altra, tramite un equilibrio del concio. Infatti bisognerà equilibrare le due forze $ F_{1} $ e $ F_{2} $ con la differenza delle spinte tra la faccia alla generica $ z $ e quella in posizione $ z + dz $.
$$ \bar{\tau}_{iz1} t_{1}dz + \bar{\tau}_{iz2} t_{2}dz + \frac{\partial \sigma_{z}}{\partial z} dz da = 0 $$
Così facendo sarà possibile mettere $ \bar{\tau}_{iz1} $ in funzione di $ \bar{\tau}_{iz2} $ (o viceversa). In ogni caso resterà un parametro e le tensioni non saranno univocamente definite. E’ l’equivalente di una struttura una volta iperstatica.
TORSIONE
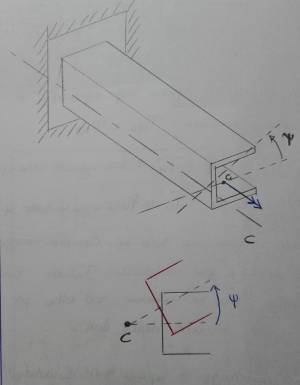
Lo studio di una struttura soggetta a torsione ha una complessità maggiore in quanto la deformazione è la composizione di una rotazione entro piano di una sezione rispetto l’altra con uno spostamento fuori piano delle sezioni. Si consideri infatti una trave incernierata con sezione a C. Se si imprime un momento torcente alla struttura, questa ruota rigidamente (spostamento entro piano) attorno all’asse del centro di taglio. A questo va aggiunto un secondo movimento (fuori piano), rappresentato da ingobbimenti della sezione. Questi ci obbligano ad utilizzare funzioni più complesse (come ad esempio l’analogia della membrana).
Problema: I punti della trave incernierati alla struttura non hanno la possibilità di movimento fuori piano. Allora la teoria in questione non è esatta. Più ci avviciniamo all’incastro e più la trave è corta, e meno la teoria è utilizzabile.
Come per il taglio, anche la torsione varia al variare del tipo della sezione, che può essere aperta o chiusa.
Torsione: sezione sottile APERTA
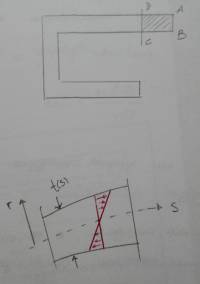
Si consideri una sezione sottile aperta, di spessore $ t(s) $ variabile (in ipotesi comunque di piccole variazioni). Si definiscono inoltre l’ascissa curvilinea $ s $ e la sua ortogonale sulla sezione, $ r $ .
Le tensioni variano linearmente a media nulla, con andamento a farfalla. Le $ \tau $ sono contemporaneamente parallele sia alle superfici esterne che al piano medio della sezione, e questo è garantito dalla PICCOLA variazione dello spessore. La possibilità di una quota media non nulla è esclusa per via degli equilibri. Infatti, se ci fosse anche un’eventuale quota media non nulla, si vede come nelle vicinanze dello spigolo $ AB $ per avere l’equilibrio, dovrà esserci una uguale tensione tagliante sulla faccia $ ABEH $. Ma questa faccia è esterna e il corpo non è caricato dall’esterno. Quindi tutte le tensioni sulla faccia $ ABEH $ sono nulle. Allora di conseguenza anche le tensioni sulla faccia $ ABCD $ saranno nulle. Quindi quota media nulla. Questo è vero per tutte le facce esterne. L’unica che potrebbe avere sollecitazione è la faccia sulla quale è stato effettuato il taglio ( $ DCFG $ ). Ma se ci fosse questa $ \tau_{m} $ , questa sarebbe l’unica. Allora si perde l’equilibrio. Quindi, si può dire con certezza che NON può esserci nessuna quota media non nulla.
In ogni caso, l’andamento disegnato (a farfalla) non è quello della tensione, ma quello della deformazione $ \gamma_{sz}(r,s) $ . Se il materiale è uniforme, il modulo di taglio è uguale su tutta la sezione e allora a quel punto si può dire che $ \tau_{sz}(r,s) $ è lineare. $ \gamma $ varia linearmente con pendenza costante lungo lo spessore.
$$ \frac{\partial \gamma_{sz}(r,s)}{\partial r} =cost $$
Tratti con spessore maggiore, subiscono deformazione maggiore. Se il corpo è omogeneo, si può dire che questo inizia a snervare da i punti a sezione maggiore. A questo punto, definito l’andamento della $ \tau $ si può calcolare il momento risultante tramite l’equilibrio alle rotazioni (rispetto un qualsiasi punto), che dovrà coincidere con il momento torcente a meno di una costante. Definito allora il momento risultante e noto $ M_{t} $ si potrà calcolare questa costante.
$$ K_{t} \simeq \frac{1}{3}\int_{0}^{l}t^{3}(s)ds $$
Per spessore costante a tratti
$$ K_{t} \simeq \frac{1}{3}\sum _{i}t^{3}_{i}l_{i} $$
Riprendendo la trave precedente, la rotazione relativa $ \psi $ è tale che
$$ \psi = \frac{M_{t}L}{K_{t}G} $$
Le tensioni massime sono situate in punti a massimo spessore (al netto di intagli e spigoli)
$$ \tau_{max} =\frac{M_{t}t_{max}}{K_{t}} $$
La formula è comunque non esatta. Nel particolare nelle vicinanze degli estremi della sezione. Nel tratto centrale le tensioni variano con andamento a farfalla (come dovrebbero). Questo vale sempre, tranne che nelle vicinanze degli estremi. In questa zona le $ \tau $ risulterebbero perpendicolari alla superficie esterna. Non è possibile. Dovranno essere parallele. Allora tutti i calcoli fatti finora cadono nell’estreme vicinanze dei terminali. La formula quindi è sempre più esatta man mano che $ b\gg t $ .
In generale comunque, calcolando il momento risultante dalla distribuzione, si ottiene solo metà del momento torcente. Le $ F $ sono grandi ma con braccio minimo. Le $ T $ sono piccole ma con molto braccio. Dovrà risultare:
$$ F \frac{t}{2} = T \frac{l}{2} $$
Si può vedere anche in un modo differente. Data la linearità della deformazione (e quindi della tensione con materiale uniforme) lungo lo spessore, si avrà che (osservando la figura) l’area dei due triangoli rossi deve coincidere con quella dei triangoli blu. Proprio per questo, man mano che aumenta $ b $ rispetto $ t $ la teoria diventa esatta.
Per $ \frac{b}{t}\simeq 10 $ l’errore è circa del $ 7 \% $.
Torsione: sezione sottile CHIUSA
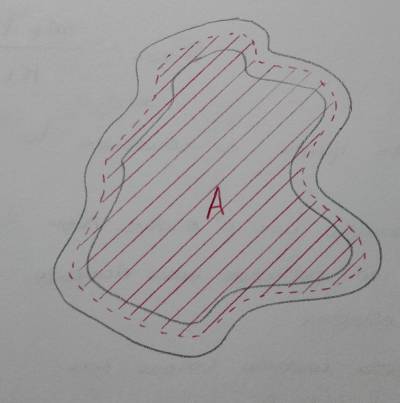
Questo studio avviene tramite la FORMULA DI BREDT. Presa la sezione sottile, se ne identifica la superficie media. Intersecando questa con ogni sezione del corpo, si ottiene una superficie di area $ A $ . La rigidezza torsionale della sezione in parete sottile chiusa è pari a quattro volte il contributo quadratico della superficie racchiusa dalla linea media, diviso l’integrale (su l ) dell’inverso dello spessore.
$$ K_{t}=\frac{4 A^{2}}{\oint \frac{1}{t}dl}\neq J_{p} $$
Se t è uniforme l’integrale non è altro che il perimetro diviso lo spessore ( $ \frac{2p}{t} $ ). Quindi:
$$ K_{t}=\frac{4 A^{2}t}{2p} $$
La rigidezza torsionale in sezione chiusa sottile, cresce linearmente con lo spessore. Per raddoppiare la rigidezza basta raddoppiare lo spessore. Nelle sezioni aperte invece variava con la terza potenza dello spessore. Questo fa capire che la rigidezza torsionale cresce faticosamente nelle sezioni sottile chiuse rispetto alle sezioni sottili aperte, ma parte da un valore iniziale nettamente maggiore ( $ K_{t_{sc}}\gg K_{t_{sa}} $ ). Si assume che le $ \tau $ siano costanti lungo lo la parete. Non c’è l’andamento a farfalla, ma solo la $ \tau $ costante lungo lo spessore. In realtà l’andamento a farfalla non è nullo, ma molto piccolo, quindi trascurabile. A livello di tensioni:
$$ \tau_{max} = \frac{M_t}{2t_{min}A} $$
Lo spessore minimo è il punto dove le $ \tau $ sono maggiori, poiché
$$ \tau t = cost $$
Nel caso di spigoli con raccordo, si considera un fattore
$$ \alpha_k = \frac{\frac{t}{r}}{ln[1,1 (1+ \frac{t}{r})]} $$
Dove si vede che per $ r \rightarrow 0 $ , $ \alpha_k \rightarrow \infty $