RICHIAMI DELLA TEORIA DELLA TRAVE: SFORZO NORMALE E MOMENTO FLETTENTE
a cura di Matteo Montagnani, Edoardo Maletti, Francesco Casini e Maria Giordano
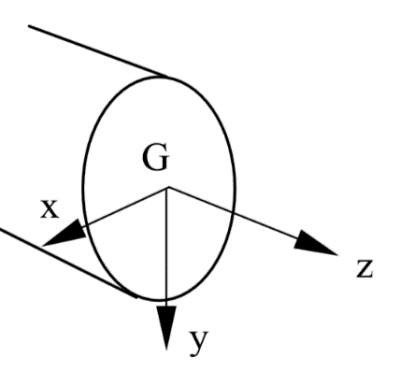
Si considerino note le caratteristiche di un corpo deformabile assimilabile a una trave come il suo asse baricentrico e le sezioni ad esso ortogonali; si stabilisce un orientamento sull’asse cosicché, per ogni concio di trave, sia possibile individuare il versore k dell’asse z il cui orientamento è concorde su ognuna delle due facce del concio preso in esame.
Si consideri un sistema di riferimento baricentrico arbitrario (x,y,z) imponendo la direzione z positiva come definito sopra; con l’ausilio di un vettore v̅ qualsiasi, quindi per definizione non parallelo all’asse baricentrico, posso andare a definire un sistema destrorso di coordinate sulla faccia di concio facendo coincidere verso e direzione della componente ortogonale alla linea baricentrica del vettore v̅ con il versore i dell’asse x e successivamente andando a definire il versore j dell’asse y ad esso perpendicolare.
Sulla faccia opposta del concio a quella considerata conviene costruire un sistema di riferimento controrientato a quello precedentemente, ovvero un sistema sinistrorso.
Supponiamo ora di caricare con un certo sistema di forze genericamente definito la trave che conseguentemente, in virtù della sua elasticità, si deforma; la deformazione avviene grazie alla trasmissione delle sollecitazioni tra una sezione e l’altra allora, ponendo F̅ il vettore forza generico agente sulla sezione considerata, possiamo pensare di considerare la forza infinitesima che agisce su di un’area infinitesima di sezione, ovvero la quantità vettoriale (dF̅)/dA che è un vettore a tre componenti finite; componenti che definiscono gli sforzi, o tensioni, e che dimensionalmente sono delle pressioni.
Chiamo allora:
- σzz o σz la componente di tensione agente sulla faccia z in direzione z
- τzx la componente di tensione agente sulla faccia normale a z in direzione x
- τzy la componente di tensione agente sulla faccia normale a z in direzione y
Per garantire l’equilibrio alla traslazione in direzione orizzontale (z) occorre che le σ delle due facce opposte siano uguali in modulo ma di verso opposto.
Per garantire l’equilibrio alla traslazione in direzione verticale (x se si osserva il cubetto sul piano (x,z), y se si osserva dal piano (y,z)) occorre che le τ delle due facce opposte siano uguali in modulo ma di verso opposto.
A questo punto occorre imporre delle τ sulla faccia superiore e su quella inferiore tali che permettano di rispettare l’equilibrio alla rotazione, tali τ saranno di modulo uguali a quelle che agiscono sulla faccia z ma tali da produrre una rotazione nel verso contrario; si noti che queste τ agiscono sulle facce x e y in direzione z, si può perciò dedurre che τzx=τxz e che τzy=τyz
Per la trave le tre tensioni σz,τxz,τyz sono definite “out of plane stress components” o componenti tensionali di interfaccia in quanto si trasmettono da una sezione a quella successiva; sono perciò identiche su due sezioni adiacenti. Le componenti σx, σy e τxy sono definite “in plane stress components”, rimangono confinate al piano della sezione e, in linea puramente teorica, potrebbero variare da una sezione alla successiva senza perciò essere trasmesse tra un concio di trave e quello adiacente (ciò avviene se non è garantita la continuità degli spostamenti da un concio al successivo); per questo motivo nello studio delle sollecitazioni saranno prese in considerazione solamente le prime.
Supponiamo di calcolare un sistema di forze equivalente a quello che agisce sulla sezione considerata esprimendolo tramite le tensioni precedentemente definite.
Posso allora andare a definire una sollecitazione di sforzo normale (N) e due sollecitazioni di taglio (Sx, Sy).
\[N = \int\int _{A} \sigma_{z}\cdot dA\]
\[S_{x} = \int\int _{A} \tau _{zx}\cdot dA\]
\[S_{y} = \int\int _{A} \tau _{zy}\cdot dA\]
Di queste solo lo sforzo normale è applicato al baricentro mentre le due sollecitazioni di taglio sono applicate al centro di taglio il che assicura l’equilibrio torsionale della trave.
Tramite le tensioni applicate alla sezione posso andare a definire anche tre momenti, presi positivi se orientati nello stesso verso degli assi della terna di riferimento, ovvero un momento torcente (Mt), avente come polo il centro di taglio C, e due momenti flettenti (Mx, My), aventi come polo il baricentro G.
\[M_{x} = \int\int _{A} \sigma _{z}\cdot y \cdot dA\]
\[M_{y} = \int\int _{A} -\sigma _{z}\cdot x \cdot dA\]
\[M_{t} =M_{z} = \int\int _{A} \left [ \tau _{zy} \cdot \left ( x-x_{c} \right )- \tau _{zx} \cdot \left ( y-y_{c} \right ) \right ] \cdot dA\]
Dove (xc; yc) sono le coordinate del centro di taglio C.
Dopo aver definito le caratteristiche di sollecitazione che vanno a sollecitare la trave occorre definire lo stato tensionale indotto da queste, se il corpo è costituito da un materiale deformabile, elastico e lineare allora è applicabile la teoria dell’elasticità, teoria che permette di ottenere delle soluzioni esatte per numerosi corpi e caricamenti.
La teoria dell’elasticità esprime gli stati tensionali e deformativi di numerosi corpi tuttavia le formule risolutive non sono sempre calcolabili con facilità o, nel caso peggiore, non presentano una soluzione univoca; per ovviare a queste problematiche sono disponibili delle formule semplificate, tali formule sono valide per le sollecitazioni di sforzo normale e di momento flettente purché il corpo sia assimilabile a una trave e siano rispettati i seguenti punti:
- La trave deve essere a sezione costante.
- La trave deve avere un asse indeformato strettamente rettilineo.
- Il caricamento della trave non deve includere dei carichi concentrati altrimenti nel punto di applicazione del carico, che solitamente è il punto più critico, la teoria non è accurata.
- Si è in assenza di sollecitazioni di taglio ovvero si è in presenza di un Mf costante. (se le sollecitazioni di taglio sono presenti allora dovrà essere sovrapposta alla soluzione flesso-estensionale una soluzione esatta capace di valutare gli effetti prodotti da una sollecitazione di taglio; solitamente, tranne che per poche sezioni, la formula risolutiva esatta per i problemi di taglio è ignota).
- Il materiale della trave deve essere omogeneo e isotropo (metalli e plastiche sono materiali omogenei e isotropi, i materiali compositi a fibra lunga no) o almeno deve essere ortotropo e il suo asse deve essere allineato secondo una direzione principale di ortotropia (un materiale è definito ortotropo se esistono tre direzione, dette direzioni principali di ortotropia, secondo le quali se il materiale è sottoposto a sforzo normale allora viene mantenuta l’ortogonalità delle superfici ovvero non si producono tensioni taglianti all’interno dell’elemento).
- I coefficienti di Poisson sono costanti lungo la sezione (in generale Ei∙νij=Ej∙νji e νij≠νji) ovvero se sul cubetto infinitesimo viene applicato una tensione trattiva questa produrrà una strizione entropiana lungo le altre due direzioni di uguale intensità.
Si noti che l’ultimo punto non rappresenta un problema per le travi costituite di materiale omogeneo ma può esserlo per quelle costituite di materiale ortotropo o per quelle costituite da più materiali (es. tubolare riempito di schiuma).
Nella realtà non si lavorerà mai con dei corpi che rispettino completamente queste ipotesi tuttavia si utilizza questa teoria semplificata per ricavare delle soluzioni esatte al netto di un errore che sarà tanto maggiore in base a quante approssimazioni sono state impiegate nello studio del corpo.
Se la teoria dell’elasticità è applicabile posso ricavare una soluzione flesso-estensionale per cui le tensioni σx, σy, τxy, τxz, τyz sono nulle e quindi la trave è sottoposta a uno stato tensionale monoassiale dove σz≠0.
In queste condizioni la deformazione assiale εz varia linearmente lungo la sezione della trave con le coordinate x e y, per cui vale la seguente:
\[\epsilon_{z}=\epsilon_{z}\left ( x;y \right )=a+b\cdot x+c\cdot y\]
In cui εz(z) = costante.
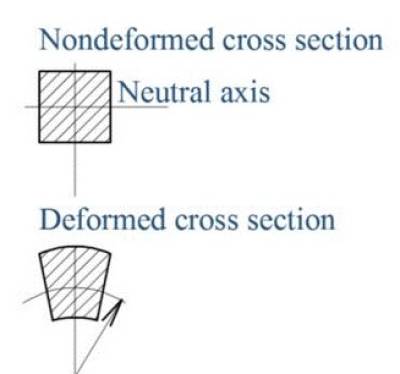
Da questa formula ricavandosi ΔL, tramite l’integrazione di εz sulla lunghezza della trave, si ottiene come risultato che le sezioni della trave rimangono piane durante la deformazione; sono quindi moti ammissibili le rototraslazioni e la strizione per effetto Poisson, mentre non lo sono quelli che provocherebbero l’ingobbimento della superficie.
I coefficienti a, b, c della formula precedente hanno un significato fisico, in particolar modo:
- - a è l’allungamento della fibra baricentrica ε̅ che coincide anche con l’allungamento medio integrale lungo la sezione.
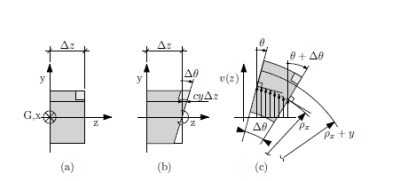
- - Per valutare c si consideri un concio di trave sul pano (y,z) di lunghezza Δz (figura a) e si prenda in esame la generica fibra alla quota y.
Sfruttando il principio della sovrapposizione degli effetti, se si considerano complessivamente le σz agenti sulla trave queste saranno equivalenti ad un caricamento che prevede una σz costante e un momento flettente orientato secondo l’asse positivo della x, in particolar modo il momento flettente produrrà una distribuzione delle σz a farfalla.
La deformata espressa nell’immagine b non è verosimile in quanto, per la teoria dell’elasticità, non possono essere applicate al concio sollecitazione di taglio che provocherebbero delle tensioni taglianti, tuttavia, queste tensioni sono presenti nella deformata (come si può vedere dalla distorsione del quadratino di colore grigio chiaro che diventa un romboide nella deformata) e, per questo motivo, si dice che è presente una sollecitazione di taglio fittizia e priva di senso fisico detta taglio spurio.
La trave, alla luce di quanto detto sopra, si deforma ingobbendo le facce superiori e inferiori (ma per ipotesi non quelle trasversali) come rappresentato dalla figura c; la quale evidenzia il mantenimento degli angoli retti del cubetto rappresentato in alto a destra nella stessa, il che implica l’assenza di distorsioni del cubetto rispettando quindi l’ipotesi di assenza delle tensioni taglianti.
Supponiamo di considerare la trave rigidamente ruotata nel piano (y,z) con una rotazione positiva dell’angolo θ. Sia poi, al contempo, deformata dalla variazione della inclinazione (rotazione differenziale) delle sezioni rappresentato da ∆θ anch’essa positiva.
Siccome siamo, per ipotesi, in linearità è lecito suppore che l’allungamento di una generica fibra sia uguale all’arco generato dal ∆θ.
Note la lunghezza iniziale del concio di trave indeformato ∆z, la rotazione relativa delle sezioni (al netto della rotazione rigida) ∆θ e detto poi Q centro di curvatura del concio di trave si può ricavare il raggio di curvatura della linea baricentrica ρx (attorno quindi all’asse x) allora risulta che ρx ∆θ=∆z.
Si nota che il raggio di curvatura della linea baricentrica ρx ha pedice x perché il concio di trave ruota attorno all’asse x.
Da queste considerazioni preliminari possiamo trovare un significato fisico per la costante b usata nella formula di εz.
Se ρx è il raggio di curvatura della linea baricentrica allora i raggi di curvatura delle altre fibre saranno ρx+y=ρ(y); si può dunque calcolare l’allungamento della fibra y-esima che vale:
\[\Delta L=l_{f}-l_{i}=\left (\rho _{x} +y\right )\cdot \Delta \Theta -\rho _{x}\cdot \Delta \Theta =y\cdot \Delta \Theta\]
La εz vale per definizione:
\[\varepsilon _{z}=\frac{\Delta L}{L_{i}}=\frac{y\cdot \Delta \Theta }{\rho _{i}\cdot \Delta \Theta }=\frac{y}{\rho _{x}}\]
Tuttavia, abbiamo ipotizzato che la componente variabile con y della forma lineare di εz sia c∙y dunque, eguagliando le 2 espressioni trovate, si ha
\[\frac{y}{\rho _{x}}= c\cdot y\]
da cui derivo
\[c=\frac{1}{\rho _{x}}\]
Detto v(z) lo spostamento (o freccia) della sezione in direzione y (ed in particolar modo del suo baricentro), posso considerare un concio di trave ora di spessore infinitesimo dz e supporre che in seguito alla rotazione rigida θ in verso orario nel piano (y,z) l’angolo θ sia approssimabile con la sua tangente, pertanto
\[tg\left ( -\Theta \right )=\frac{sin\left ( -\Theta \right )}{cos\left ( -\Theta \right )}=\frac{dv}{dz}\cong -\Theta\]
Da cui, con un errore del primo ordine affermo che
\[\frac{dv}{dz}= -\Theta\]
Ricordando poi che (passando a quantità infinitesime rispetto alla trattazione sopra) si ha
\[\frac{d\Theta }{dz}= \frac{1}{\rho_{x} }\]
Sostituendo si ottiene
\[\frac{d^{2}v }{dz^{2}}= \frac{d\left (-\Theta \right ) }{dz}=-\frac{1}{\rho_{x} }\]
Questa equazione lega lo spostamento della trave in direzione y con la conseguente curvatura che esso determina al variare della posizione z nel concio (e di conseguenza nella trave).
- In maniera analoga a c si può calcolare b osservando la deformata della trave sul piano (x,z) tenendo conto del fatto che ora la rotazione della sezione deve essere antioraria affinché sia diretta come le y positive del sistema di riferimento.
Da ciò si ricava che b=-1/ρy> in cui il segno meno è dovuto alla rotazione antioraria, ma comunque positiva, attorno all’asse y (∆l=-x∙∆Φ).
Quindi
\[\varepsilon _{z}=\bar{\varepsilon }-\frac{1}{\rho _{y}}\cdot x+\frac{1}{\rho _{z}}\cdot y\]
Si consideri ora la faccia frontale della trave ovvero quella appartenente al piano (x,y), essa si deformerà per effetto Poisson ed in particolar modo se il materiale di cui è composta la trave è omogeneo avremo che εx=εy=-ν∙εz; questa formula evidenzia appunto il comportamento dei materiali di reagire mediante una strizione ad un allungamento in direzione assiale.
Consideriamo per semplicità una trave soggetta solo a momento flettente in direzione x negativo; questo caricamento prevede la formazione di una farfalla di σ che saranno trattive per i punti in cui y < 0 mentre saranno compressive per y > 0.
In queste condizioni avremo che la εy è praticamente trascurabile in quanto sulla fibra verticale la disposizione a farfalla annulla la sigma media, si provocano cioè solo allungamenti (dove vi è compressione) o accorciamenti (dove vi è trazione) locali.
($ \sigma $ in che direzione?, $\sigma_z$, l'unica non nulla. È forse più semplice dire che le deformazioni entro piano sono derivate per effetto Poisson, es. $\epsilon_x=\epsilon_y=-\nu\epsilon_z$, come scritto sopra, e lasciare al lettore il giudicarle trascurabili o meno; non sono in effetti termini infinitesimi di ordine superiore alle $\epsilon_z$, ma dello stesso ordine. NdEB.)
Per quel che concerne εx avremo un allungamento delle fibre orizzontali sopra all’asse neutro (in compressione) mentre quelle in trazione si accorceranno.
Al fine di mantenere gli angoli durante la deformazione, in quanto si è in assenza di tensioni taglianti, la trave assumerà la forma a doppia sella rappresentata in figura; la deformazione assunta prende il nome di rotazione anticlastica.
Noto εz, dalla legge di Hooke uniassiale si ricava l’andamento delle σz nella sezione:
\[\sigma _{z}=E_{z}\cdot \varepsilon _{z}=E_{z}\cdot \left ( \bar{\varepsilon }-\frac{1}{\rho _{y}}\cdot x+\frac{1}{\rho _{z}}\cdot y\ \right )\]
Che è veritiero solo se Ez è costante lungo la sezione ovvero se la trave non è composta da più materiali.
Dalla formula della σz si ottengono le sollecitazioni di sforzo normale e di momento flettente con le definizioni precedenti:
\[N = \int\int _{A} \sigma_{z}\cdot dA=\bar{EA}\cdot \bar{\varepsilon }\]
\[M_{x} = \int\int _{A} \sigma _{z}\cdot y \cdot dA= \bar{EJ_{xx}}\cdot\frac{1}{\rho _{x}} -\bar{EJ_{xy}}\cdot\frac{1}{\rho _{y}}\]
\[M_{y} = \int\int _{A} -\sigma _{z}\cdot x \cdot dA= \bar{EJ_{yy}}\cdot\frac{1}{\rho _{y}} -\bar{EJ_{xy}}\cdot\frac{1}{\rho _{x}}\]
In cui:
\[\bar{EA} = \int\int _{A} E _{z}\left (x;y \right ) \cdot dA\]
\[\bar{EJ_{xx}} = \int\int _{A} E _{z}\left (x;y \right )\cdot y^{2} \cdot dA\]
\[\bar{EJ_{yy}} = \int\int _{A} E _{z}\left (x;y \right )\cdot x^{2} \cdot dA\]
\[\bar{EJ_{xy}} = \int\int _{A} E _{z}\left (x;y \right )\cdot x\cdot y \cdot dA\]
La presenza del termine contenente Jxy è dovuto al fatto che non è detto che gli assi x e y siano principali d’inerzia (si noti che se uno dei due assi appartiene a un piano di simmetria della sezione della trave allora i due assi sono principali d’inerzia e quindi Jxy=0).
Le due componenti (-(EJxy)∙1/ρx) e (-(EJxy)∙1/ρy) delle equazioni dei momenti flettenti rappresentano il prodotto tra la curvatura della sezione e i momenti misti (detti centrifughi o di deviazione); questi termini sono responsabili di un’incurvatura dell’asse neutro. Per esempio, applicando un Mx ad una trave per la cui sezione gli assi x ed y non risultano principali di inerzia, questa si fletterà sul piano (y,z) e si incurverà sul piano (x,z).
Solitamente le sollecitazioni applicate alla trave sono note a priori, perché ricavabili dal caricamento della struttura, mentre sono incognite le rotazioni della trave allora mettendo a sistema le formule dei momenti flettenti posso ricavarmi 1/ρx e 1/ρy.
Ottengo allora il sistema lineare 2×2
\[\left\{\begin{matrix} M_{x}= \bar{EJ_{xx}}\cdot\frac{1}{\rho _{x}} -\bar{EJ_{xy}}\cdot\frac{1}{\rho _{y}}\\ M_{y}= \bar{EJ_{yy}}\cdot\frac{1}{\rho _{y}} -\bar{EJ_{xy}}\cdot\frac{1}{\rho _{x}} \end{matrix}\right.\]
Equivalente, in forma matriciale a
\[\begin{bmatrix} M_{x}\\ M_{y} \end{bmatrix} = \begin{bmatrix} \bar{EJ_{xx}} & -\bar{EJ_{xy}} \\ -\bar{EJ_{xy}} & \bar{EJ_{yy}} \end{bmatrix} \cdot \begin{bmatrix} \frac{1}{\rho_{x}}\\ \frac{1}{\rho_{y}} \end{bmatrix}\]
La matrice è non singolare essendo quelle quantità momenti di inerzia moltiplicati per modulo di Young, dunque posso invertirla e scrivere
\[\begin{bmatrix} \frac{1}{\rho_{x}}\\ \frac{1}{\rho_{y}} \end{bmatrix} = \begin{bmatrix} \bar{EJ_{xx}} & -\bar{EJ_{xy}} \\ -\bar{EJ_{xy}} & \bar{EJ_{yy}} \end{bmatrix}^{-1} \cdot \begin{bmatrix} M_{x}\\ M_{y} \end{bmatrix}\]
\[\begin{bmatrix} \frac{1}{\rho_{x}}\\ \frac{1}{\rho_{y}} \end{bmatrix} = \frac{1}{\bar{EJ_{xx}}\cdot\bar{EJ_{yy}}- \bar{EJ_{xy}}^{2} } \begin{bmatrix} \bar{EJ_{xx}} & \bar{EJ_{xy}} \\ \bar{EJ_{xy}} & \bar{EJ_{yy}} \end{bmatrix} \cdot \begin{bmatrix} M_{x}\\ M_{y} \end{bmatrix}\]
da cui è immediato ricavare i valori delle 2 curvature, direttamente sostituibili nella espressione della εz
\[\frac{1}{\rho_{x}} = \frac{M_{x}\cdot\overline{EJ}_{yy}+M_{y}\cdot\overline{EJ}_{xy} }{\overline{EJ}_{xx}\cdot\overline{EJ}_{yy}- \overline{EJ}_{xy}^{2} }\]
\[\frac{1}{\rho_{y}} = \frac{M_{x}\cdot\overline{EJ}_{xy}+M_{y}\cdot\overline{EJ}_{xx} }{\overline{EJ}_{xx}\cdot\overline{EJ}_{yy}- \overline{EJ}_{xy}^{2} }\]
Se x e y sono assi principali d’inerzia, allora:
\[\frac{1}{\rho_{x}} = \frac{M_{x} }{\overline{EJ_{xx}} }\]
\[\frac{1}{\rho_{y}} = \frac{M_{y} }{\overline{EJ_{yy}} }\]
Se il modulo di Young è costante su tutta la sezione, si possono riscrivere le formule delle rotazioni come:
\[\frac{1}{\rho_{x}} = \frac{M_{x}\cdot J_{yy} + M_{y}\cdot J_{xy} } {E\cdot \left (J_{xx}\cdot J_{yy}- J_{xy}^{2} \right )}\]
\[\frac{1}{\rho_{y}} = \frac{M_{x}\cdot J_{xy} + M_{y}\cdot J_{yy} } {E\cdot \left (J_{xx}\cdot J_{yy}- J_{xy}^{2} \right )}\]
Se entrambe le condizioni sono vere, allora:
\[\frac{1}{\rho_{x}} = \frac{M_{x}} {E\cdot J_{xx}}\]
\[\frac{1}{\rho_{y}} = \frac{M_{y}} {E\cdot J_{yy}}\]
Ricavate le curvature si può quindi andare a definire lo stato tensionale della sezione in funzione dei momenti e delle caratteristiche del materiale (E) e della sezione (J)
\[\sigma _{z}=E_{z}\cdot \left ( \bar{\varepsilon }-\frac{M_{x}\cdot\bar{EJ_{xy}}+M_{y}\cdot\bar{EJ_{xx}} }{\bar{EJ_{xx}}\cdot\bar{EJ_{yy}}- \bar{EJ_{xy}}^{2} }\cdot x+\frac{M_{x}\cdot\bar{EJ_{yy}}+M_{y}\cdot\bar{EJ_{xy}} }{\bar{EJ_{xx}}\cdot\bar{EJ_{yy}}- \bar{EJ_{xy}}^{2} }\cdot y \right )\]
Si noti che se il materiale è omogeneo il punto a stato tensionale più critico è anche quello a stato deformativo più critico ovvero quel punto che nella sezione si trova alla distanza massima dall’asse neutro.
Se ε̅ =0 allora l’asse neutro passa per il baricentro; in queste condizioni, considerando un materiale omogeneo isotropo (E = costante) e avendo preso x e y principali di inerzia si ottiene
\[\sigma _{z}=\frac{M_{x} }{EJ_{xx}}\cdot y-\frac{M_{y} }{EJ_{yy}}\cdot x\]
Appunti in PDF