Indice
Riferimenti: The Finite Element Method da Boresi Schmidt, 5a edizione.
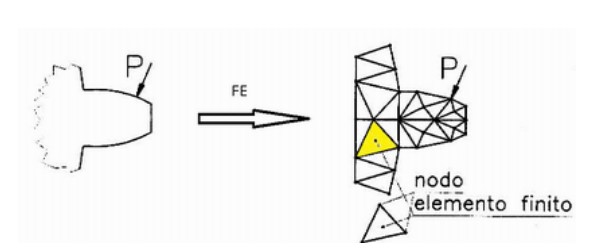
ELEMENTO TRIANGOLARE A TRE NODI
Prendiamo in esame la nostra struttura, ovvero il dente di una ruota dentata. Il problema prevede un incastro applicato alla base del dente, per isolare lo stesso dal resto della ruota dentata, una forza di contatto che è risultante delle pressioni di contatto dente-dente e infine abbiamo definito lo stato tensionale e deformativo di un volumetto di materiale localizzato sul raccordo del dente.
Tramite l'approccio agli elementi finiti siamo in grado di ricavare dagli spostamenti le deformazioni e dalle deformazioni le tensioni, quindi gli spostamenti sono le nostre incognite principali. Esiste una formulazione duale alle tensioni, la quale parte dall’equazione di equilibrio sulle tensioni, per ricavare tramite legame elastico le deformazioni e infine tramite equazioni di congruenza, gli spostamenti. Quindi nella teoria dell’elasticità l’approccio tipico è quello alle tensioni, mentre nella teoria agli elementi finiti l’approccio è agli spostamenti.
FEM – DISCRETIZZAZIONE DEL DOMINIO CONTINUO
Il problema si riduce a conoscere gli spostamenti di ogni punto della struttura. Definiamo un sistema di riferimento (x,y) che ci aiuterà nel piano a definire i punti di interesse, e per ogni punto P della struttura il nostro problema agli spostamenti si riconduce a conoscerne:
- u che abbiamo chiamato spostamento in direzione x;
- v che abbiamo chiamato spostamento in direzione y;
- w che abbiamo chiamato spostamento in direzione z.
Questi spostamenti sono funzione di x,y ed eventualmente di z.
Quindi in nostro problema si riconduce a ricavare gli spostamenti dei punti del dominio, ma i punti del dominio sono infiniti, per cui abbiamo infinite incognite, quindi non riusciamo a trattarlo con un calcolatore, poiché il calcolatore possiede una memoria finita.
Per ovviare si procede suddividendo il nostro dominio in una serie di sottodomini di forma triangolare, infatti è possibile suddividere una qualunque figura piana poligonale in composizioni di triangoli. Tuttavia la nostra struttura in esame non è poligonale, quindi si accetta un “errore di discretizzazione del contorno” dovuto al fatto che si approssimano tratti curvi con segmenti rettilinei.
Questi sottodomini determinano una “Partizione” e presentano le seguenti proprietà:
- l’unione dei sottodomini restituisce il dominio originale di partenza;
- i sottodomini hanno intersezione nulla l’uno con l’altro, cioè non si sovrappongono.
Per cui nel far ciò accettiamo che il contorno del dominio originale sia rappresentato solo in forma approssimata; ciò, come già detto, dà luogo ad un ”errore di discretizzazione” cioè uno scostamento rispetto alla soluzione effettiva legato alla rappresentazione del contorno (boundary).
Tale errore di discretizzazione si riduce se invece di partizionare degli elementi in una dimensione caratteristica che posso chiamare h (lato dell’elemento triangolare), utilizzo come dimensione caratteristica una dimensione molto più piccola (h/10, h/100) oppure utilizzando elementi con lati curvilinei.
Dopodiché continuando con la nostra triangolazione del dominio ci accorgiamo di aver definito una specie di struttura reticolare: un tentativo potrebbe essere quello di supporre che il dente si comporti come una struttura ad aste. Tuttavia la discretizzazione di tipo reticolare non si dimostra adatta a descrivere un componente continuo infatti, il materiale esistente tra le maglie irrigidisce molto la struttura e ciò non è stimabile con un approccio ad aste. Allora si utilizzano i FEM in cui si discretizza il dominio attraverso elementi finiti 2D, dove l’effetto irrigidente del materiale interno viene considerato tramite un approccio energetico.
Però della struttura reticolare manteniamo il concetto di nodi di collegamento tra elemento ed elemento, ossia supponiamo che ognuno degli elementi triangolari si connetta agli altri per collegamento dei vertici: gli elementi interagiscono solamente tramite forze sui vertici, ossia non c’è alcuna interazione diretta tra lati contigui.
CALCOLO DEGLI SPOSTAMENTI NODALI
I nodi hanno il vantaggio rispetto a tutti gli altri punti del dominio:
- di essere in numero finito;
- di essere numerosi a piacere, così il metodo risulta essere molto flessibile rispetto alle esigenze di avere calcolo.
Occupiamoci del problema piano, definendo come incognite le due funzioni spostamento
$u= u\left ( x,y \right )$
$v= v\left ( x,y \right )$
Considerando un sistema con N nodi, le nostre incognite saranno $u_{i}$ e $v_{i}$, spostamenti del nodo i-esimo con $i= 1,...,N$ .
Con questa formulazione ogni elemento avrà $6$ g.d.l , ognuno dei quali rappresenta un’incognita del problema. Tuttavia esistono casi specifici in cui agli spostamenti nodali devo aggiungere altre quantità.
Per esempio gli “Herman-Elements”, hanno $2$ g.d.l. per ogni nodo nel piano e 3 nello spazio, ed in più hanno un g.d.l di pressione idrostatica campionata al centroide di ogni elemento.
SPOSTAMENTO DEGLI ELEMENTI – INTERPOLAZIONE LINEARE
A questo punto è necessario definire delle regole per ricavare dagli spostamento nodali lo spostamento di tutti i punti interni ad ogni sottodominio triangolare .
Consideriamo allora un elemento triangolare i cui nodi vengono denominati $i,j,k$ ed un generico punto $P$ all’interno di esso.
Lo spostamento in direzione $x$ del punto interno $P$ si definisce come interpolazione lineare, nel piano $(x,y)$, dei valori di spostamento lungo $x$ dei nodi $i,j,k$.
Quindi $u_{p}$ è definito come interpolazione lineare degli spostamenti $u_{i}$, $u_{j}$, $u_{k}$.
Analogamente $v_{p}$ è definito come interpolazione lineare degli spostamenti $v_{i}$, $v_{j}$, $v_{k}$.
Se lo spostamento interno è definito per interpolazione lineare, allora è una funzione lineare definita nella forma:
$u(x,y) = \alpha _{1} +\alpha _{2}x + \alpha _{3}y$
$v(x,y) = \alpha _{4} + \alpha _{5}x + \alpha _{6}y$
Affinché la funzione sia lineare, tali coefficienti debbono essere costanti in $x,y$: quindi devono valere per ogni punto dell’elemento e dunque in particolare anche ai nodi.
Scriviamo le funzioni sui nodi $i,j,k$.
Lo spostamento lungo x del nodo i sarà:
$u_{i}(x,y) = \alpha _{1} +\alpha _{2}x_{i} + \alpha _{3}y_{i}= u_{i}$
Analogamente per gli spostamento lungo $x$ dei nodi $j,k$
$u_{j}(x,y) = \alpha _{1} +\alpha _{2}x_{j} + \alpha _{3}y_{j}= u_{j}$
$u_{k}(x,y) = \alpha _{1} +\alpha _{2}x_{k} + \alpha _{3}y_{k}= u_{k}$
Quindi ottengo un sistema di $3$ equazioni nelle $3$ incognite $\alpha _{1}$, $\alpha _{2}$,$\alpha _{3}$ :
$$ \begin{cases} & u_{i} = \alpha_{1}+\alpha_{2}x_i+\alpha_{3}y_i\\ &u_{j} = \alpha_{1}+\alpha_{2}x_j+\alpha_{3}y_j\\ &u_{k} = \alpha_{1}+\alpha_{2}x_k+\alpha_{3}y_k\\ &\end{cases} $$
Scriviamo tale sistema in forma matriciale, evidenziando la matrice $3x3$ dei coefficienti, il vettore delle incognite $α$ e il termine noto $u$ :
$$\begin{bmatrix} 1 &x_i &y_i \\ 1&x_j &y_j \\ 1&x_k &y_k \end{bmatrix}\cdot \begin{bmatrix} \alpha _1\\ \alpha _2\\ \alpha _3 \end{bmatrix}= \begin{bmatrix} u_i\\ u_j\\ u_k \end{bmatrix}$$
NB. La matrice di sistema è strettamente legata all’area dell’elemento, in quanto prendendo un triangolo di nodi $i, j, k$ le cui coordinate sono $(x_{i},y_{i})$, $(x_{j},y_{j})$, $(x_{k},y_{k})$ l’area del triangolo (Simplesso 2D), può essere ricavata come:
$$ a=\begin{vmatrix} 1 &1 &1 \\ x_{i} & x_{j} &x_{k} \\ y_{i} & y _{j} &y _{k} \end{vmatrix}\frac{1}{2!} $$
Osserviamo che c’è una similitudine tra la matrice di sistema e $(*)$; in particolare la matrice di sistema è la trasposta di $(*)$.
$$\begin{bmatrix} 1 &x_i &y_i \\ 1&x_j &y_j \\ 1&x_k &y_k \end{bmatrix}= \begin{bmatrix} 1 &1 &1 \\ x_i& x_j&x_k \\ y_i& y_j &y_k \end{bmatrix}\left ( \ast \right )$$
Per cui se il determinante $(*)$ è uguale a zero significa che anche il determinante della matrice di sistema è nullo; Quindi stiamo bene attenti a creare un triangolo di area non nulla, cosicché il determinante della matrice di sistema sarà non nullo, per cui il sistema avrà una e una sola soluzione. Osservazione: considerando invece un tetraedro (Simplesso $3D$) con $4$ nodi $i, j, k, l$, esso avrà volume:
$$ V=\begin{vmatrix} 1 & 1 &1 &1 \\ x_{i }& x_{j} & x_{k} &x_{h} \\ y_{i} & y_{j} & y_{k} &y_{h} \\ z_{i} & z_{j} &z_{k} & z_{h} \end{vmatrix}\frac{1}{3!} $$
Tale volume è positivo, se ponendoci come osservatori sul quarto nodo $l$, osserviamo la base enumerata come $i, j, k$ in senso antiorario; cambiando la numerazione varierà l’ordine di tali colonne, cosicché il determinante può cambiare segno.
Grazie ad un software d calcolo, è possibile determinare i coefficenti $alpha$:
$\alpha _{1}=\alpha _{1}\left ( u_{i},u_{j},u_{k},v_{i},v_{j},v_{k} \right )$
$\alpha _{2}=\alpha _{2}\left ( u_{i},u_{j},u_{k},v_{i},v_{j},v_{k} \right )$
$\alpha _{3}=\alpha _{3}\left ( u_{i},u_{j},u_{k},v_{i},v_{j},v_{k} \right )$
ottenendo l’interpolazione lineare desiderata.
FORMULA GEOMETRICA DI INTERPOLAZIONE LINEARE
E’ una forma più semplice per definire l’interpolazione lineare, per impostare e risolvere il sistema, in maniera geometrico-grafica.
Supponiamo di avere il nostro triangolo di nodi $i, j, k$ e di avere una funzione qualunque definita nei suoi valori nodali $i, j, k$, rispettivamente come $F_{i},F_{j},F_{k}$.
Dato il punto interno $P$, il nostro obiettivo è determinare $F$, cioè il valore interpolato della funzione nel punto $P$ , noti i valori sui nodi.
La costruzione geometrica è la seguente:
costruisco tre sotto triangoli interni al triangolo originario tirando dei segmenti dai vertici al punto $P$, nominando i sotto-elementi sulla base del nodo che non contengono. Ad esempio battezzo l’area $a_{i}$ quella che contiene i nodi $k$ e $j$ ma non $i$. Allo stesso modo battezzo le aree $a_{j}$ relativo al nodo $j$ e $a_{k}$ relativo al nodo $k$.
Inoltre l’area di tali triangoli abbiamo visto che è abbastanza facile da ricavare: ad esempio:
$$ a=\begin{vmatrix} 1 &1 &1 \\ x_{i} & x_{j} &x_{k} \\ y_{i} & y _{j} &y _{k} \end{vmatrix}\frac{1}{2!} $$
A questo punto posso dire che l’area originaria a del triangolo, senza alcun pedice, è uguale a:
$a=a_{i}+a_{j}+a_{k}$
Di seguito due relazioni che ci consentono di verificare se il punto P è interno o esterno all’elemento:
- Se $\left | a \right |= \left | a_{i} \right |+\left | a_{j} \right |+\left | a_{k} \right |$ allora P è un punto interno al triangolo;
- Se $\left | a \right |< \left | a_{i} \right |+\left | a_{j} \right |+\left | a_{k} \right |$ allora P è un punto esterno al triangolo.
Una volta isolate tale aree possiamo verificare che il valore della funzione al punto $P$ sarà una media pesata del valore della funzione nei diversi nodi $i, j, k$ con pesi corrispondenti all’area dei sotto triangoli:
$F_{p}= f_{i}\cdot\frac{a_{i}\left ( x,y \right ) }{a}+f_{j}\cdot\frac{a_{j}\left ( x,y \right ) }{a}+f_{k}\cdot\frac{a_{k}\left ( x,y \right ) }{a}$
$F_{p}$ è la funzione di interpolazione lineare (di estrapolazione), possiamo usare tale espressione sia per punti interni (esterni) al triangolo.
Ora per vedere se funziona prendiamo un punto $P$ che si avvicina di molto al nodo $i$, il triangolo associato al nodo P ha un’area che è quasi uguale all’area del triangolo totale, in particolare se il punto P viene a coincidere con il nodo $i$, tale area relativa al nodo $i$ sarà coincidente con l’area totale $a_{i}(x,y)=a$ e le aree degli altri triangoli si annullano.
Quindi la $F_{p}$ nel caso in cui il punto $P$ è molto vicino al nodo $i$ sarà:
$F_{p} \simeq F_{i}$
Cosicché è garantita la continuità: la funzione di interpolazione campionata su di un punto in prossimità del nodo è prossima al valore al nodo.
Definiamo le funzioni peso:
$N_{i}(x,y)=\frac{a_{i}(x,y)}{a}$
$N_{j}(x,y)=\frac{a_{j}(x,y}{a}$
$N_{k}(x,y)=\frac{a_{k}(x,y)}{a}$
Ad esempio,utilizzando la regola di Sarrus:
$$ N_i = \frac{ \begin{vmatrix} 1 & 1 & 1\\ x & x_j & x_k \\ y & y_j & y_k \end{vmatrix} }{ \begin{vmatrix} 1 & 1 & 1\\ x_i & x_j & x_k \\ y_j & y_j & y_k \end{vmatrix} }=\frac {x_j y_k+x_k y +x y_j -y x_j -y_j x_k -y_k x} {x_j y_k+x_k y_i +x_i y_j -y_i x_j -y_j x_k -y_k x_i} $$
Si noti come $i$ termini $x$ ed $y$ al denominatore e al numeratore appaiano sempre alla prima potenza , motivo per cui tali peso associato al nodo $i$ così come quelli associati ai nodi $j$ e $k$ sono forme lineari.
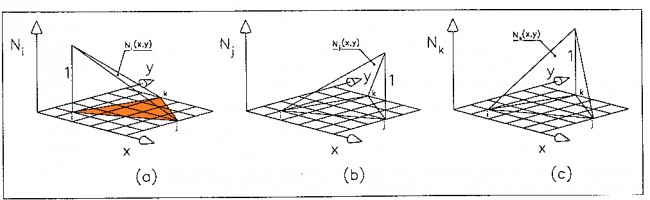
La funzione di forma (base nodo1) ) dell’elemento $N_{i}$ è tale per cui:
- se la campiono sul nodo $i-esimo$ vale $1$
- se la campiono sugli altri due nodi $j$ e $k$ vale $0$
Allo stesso modo la funzione $N_{j}$, peso associato al nodo $j$:
- se la campiono sul nodo $j-esimo$ vale $1$
- se la campiono sugli altri due nodi $i$ e $k$ vale $0$
Si noti dall’immagine che le funzioni di forma sono delle porzione di piano inclinato.
In generale le funzioni di forma hanno tali caratteristiche:
- la somma delle $3$ su ogni punto vale sempre $1$;
- se abbiamo i $3$ valori della funzione ai $3$ vertici del triangolo, l’interpolazione lineare di quei $3$ valori al baricentro vale $1/3$ per ciascuno valore della funzione ai vertici.
CALCOLO DEGLI SPOSTAMENTI
Anziché considerare l’interpolazione di una funzione generica, consideriamo il problema agli spostamenti all’interno del triangolo:
$u(x,y)=N_{i}(x,y)u_{i}+N_{j}(x,y)u_{j}+N_{k}(x,y)u_{k}$
$v(x,y)=N_{i}(x,y)v_{i}+N_{j}(x,y)v_{j}+N_{k}(x,y)v_{k}$
Si può estendere il risultato trovato per elementi con un numero maggiore di nodi:
$U(x,y)=\sum_{l=1}^{M}N_{l}(x,y)u_{l}(x,y)$
Considerando che le funzioni $u(x,y)$ e $v(x,y)$ sono lineari, esse possono essere viste come un vettore $δ$ premoltiplicato per una matrice $N(x,y)$,che possiamo scrivere in questo modo: dimensionalmente abbiamo tante righe quanto questo termine $u(x,y)$ e tante colonne quanto quest’altro elemento $δ$, quindi è una $2$ righe e $6$ colonne.
$$\begin{bmatrix} U(x,y)\\ V(x,y) \end{bmatrix}= \begin{bmatrix} N_i(x,y) &0 &N_j(x,y) &0 &N_k(x,y) &0 \\ 0& N_i(x,y)& 0& N_j(x,y)& 0& N_k(x,y) \end{bmatrix}\cdot \begin{bmatrix} u_i\\ v_i\\ u_j\\ v_j\\ u_k\\ v_k \end{bmatrix}$$
In forma compatta :
$$U(x,y)=N(x,y)\delta$$
Osservazione: $U(x,y)$ non ha nessun pedice, poiché non è associato a nessun nodo, ma è relativo ad un punto generico dell’elemento. Il vettore $δ$ raccoglie tutti i g.d.l dell’elemento. In questo modo abbiamo definito gli spostamenti dei punti di ogni punto della struttura $u(x,y)$ in funzione degli spostamenti nodali. Quindi dalle funzioni di forma dell’elemento è possibile ricavare facilmente delle funzioni di forma di struttura. Le funzioni di forma di struttura di un dato nodo hanno sempre le caratteristiche:
- valgono 1 sul nodo a cui sono associate;
- valgono 0 su tutti gli altri nodi.
Sulla struttura però tali funzioni non sono più lineari, ma sono definite lineari a tratti, oppure lineari su di un sottodominio. Quindi le funzioni di forma definite lineari sull’elemento, danno luogo a funzioni di forma sulla struttura lineari a tratti. Da qui notiamo che lo spostamento di ogni punto della struttura è definito come funzione di forma della struttura per gli spostamenti del nodo a cui sono associate:
Dato un generico nodo $l$ della struttura, si può ricavare l’espressione dello spostamento di un generico punto della struttura come :
$$U(x,y)=\sum_{l=1}^{M}N_{l}(x,y)u_{l}(x,y)$$
per cui la stessa cosa che abbiamo fatto all’elemento possiamo estenderla alla struttura considerando le funzioni di forma di struttura derivate dalle funzioni di forma dell’elemento. In particolare, la funzione di forma della struttura sarà lineare a tratti se l'elemento è lineare, o quadratica se l'elemento è curvo. Lo spostamento di un generico punto $(x,y)$ della struttura viene modulato tramite dei pesi, che sono gli spostamenti nodali.
Ovviamente risulterà che questo spostamento sarà pure una funzione lineare a tratti.
Possiamo riassumere i passaggi svolti in questo modo:
- isolo dei sottodomini triangolari;
- definisco come incognite rilevanti lo spostamento dei nodi di tali sottodomini triangolari,all’interno dei sottodomini uso delle interpolazioni lineari che sulla struttura diventano lineari a tratti determino che gli spostamenti che posso rappresentare, sono tutti della famigli lineari a tratti.
Si nota che la forma lineare a tratti è un grosso vincolo, nel senso che nessuno degli elementi potrà mai incurvarsi, poiché se procedo per interpolazione lineare la deformata del triangolo dovuta agli spostamenti nodali rimarrà in configurazione rettilinea.
Quindi tutti i moti che non rispettino tale forma di linearità sono vietati, ciò porta ad un inevitabile irrigidimento della struttura. Di conseguenza i risultati tenderanno a sottostimare l’energia di deformazione nonché la rigidezza a carico imposto.
A questo punto le nostre funzioni di forma inseriscono un secondo tipo di errore che viene chiamato $$”formulation error”$$ tipicamente il più grande che c’è nella trattazione. Esso può essere ridotto con le stesse metodologie di riduzione usate per l’errore di discretizzazione. Ovviamente l’errore sarebbe zero, solo se avessimo infiniti nodi, cioè infiniti g.d.l. A questo, si aggiunge l’errore numerico dovuto alla precisione di calcolo implementata al calcolatore.
CALCOLO DELLE DEFORMAZIONI
Considero la relazione:
$U(x,y)=N(x,y)\delta$
avendo solo spostamenti entro il piano, introduciamo le ipotesi semplificative di tensione e deformazione piana:
DEFORMAZIONE PIANA
$\varepsilon _{x},\varepsilon _{y},\gamma _{xy}$
$\varepsilon _{z}=\gamma _{xz}=\gamma _{zy}=0$ (ipotesi semplificativa)
TENSIONE PIANA
Il competitor di tale ipotesi semplificativa è un’altra ipotesi semplificativa che dice che:
$\varepsilon _{z}=-\nu (\varepsilon _{x}+\varepsilon _{y})$ associata all’ipotesi che $\sigma _{z}=0$
$\gamma _{xz}=\gamma _{yz}=0$ associata all’ipotesi che $\tau _{zx}=\tau _{zy}=0$
Possiamo ricavare le componenti di deformazione εx, εy, γxy dagli spostamenti utilizzando un operatore matriciale differenziale:
$$\begin{bmatrix} \varepsilon _x\\ \varepsilon _y\ \\ \gamma _{xy} \end{bmatrix}= \begin{bmatrix} \frac{\partial }{\partial x}&0 \\ 0&\frac{\partial }{\partial y} \\ \frac{\partial }{\partial y}&\frac{\partial }{\partial x} \end{bmatrix}\cdot \begin{bmatrix} U(x,y)\\ V(x,y) \end{bmatrix}= L\cdot N(x,y )\cdot \delta $$
$L$ è una matrice $3X2$, nonchè operatore differenziale che contiene gli operatori di derivazione. Tale operatore differenziale posso applicarlo direttamente alle funzioni di forma, ottenendo una matrice $B$, che lega le deformazioni agli spostamenti.
$$B=\begin{bmatrix} \frac{\partial }{\partial x}&0 \\ 0&\frac{\partial }{\partial y} \\ \frac{\partial }{\partial y}&\frac{\partial }{\partial x} \end{bmatrix}\cdot \begin{bmatrix} N_i(x,y) &0 &N_j(x,y) &0 &N_k(x,y) &0 \\ 0& N_i(x,y)& 0& N_j(x,y)& 0& N_k(x,y) \end{bmatrix}= \begin{bmatrix} \frac{\partial N_i}{\partial x} &0 &\frac{\partial N_j}{\partial x} &0 &\frac{\partial N_k}{\partial x} &0 \\ 0& \frac{\partial N_i}{\partial y}& 0& \frac{\partial N_j}{\partial y}& 0& \frac{\partial N_k}{\partial y}\\ \frac{\partial N_i}{\partial y}& \frac{\partial N_i}{\partial x}& \frac{\partial N_j}{\partial y}& \frac{\partial N_j}{\partial x}& \frac{\partial N_k}{\partial y}& \frac{\partial N_k}{\partial x}\end{bmatrix}$$
La matrice $B$ è una $3x6$ i quali elementi sono costanti in quanto le funzioni di forma sono lineari in $x$ e $y$, per cui la loro derivate sono costanti.
Se la matrice $B$ non è funzione di $(x,y)$ il vettore delle deformazioni $ε$ è uguale ad una matrice costante per il vettore degli spostamenti ai nodi, il quale è costante all’interno dei triangoli, per cui le deformazioni sull’elemento sono anch’esse costanti.
L’elemento triangolare ha un nome codificato internazionale che è $CST$ (Constant strain triangle).
Infine le tensioni, essendo funzioni lineari delle deformazioni, sono anch’esse costanti sul triangolo, quindi in tali elementi triangolari lo stato tensionale è uniforme.
Autori, note e ringraziamenti
Autori
Fabrizio Fiore, mat. 97210, Giovanni Gianforcaro, mat. 104387, Francesco Russo, mat. 219199 , Remo Piccolo, mat. .
Tabella di monitoraggio carico orario
PATTUME
Spostare qui il materiale caricato dal docente non utilizzato a lezione o non inerente alla trattazione.




Discussione
REVISORE 1 Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste. Vi sono delle imprecisioni:
relativa matrice calcolata dal punto di inizio P interno al triangolo;
maiuscolo e precisare che sono calcolate come media pesata;
è stato utilizzato il metodo del Sarrus;
che N è funzione di forma della struttura, lineare a tratti se elemento è lineare, o quadratica se elemento è curvo;
Il testo proposto è coerente con gli appunti personali del revisore?
SI il testo è coerente con i miei appunti
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Sarebbe utile una foto di una trave retta e successivamente incurvata, per esprimere il grosso vincolo che rappresenta la forma lineare a tratti
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
Si
Ore dedicate a questa revisione
2 ore