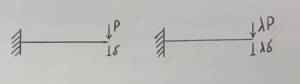Nella precedente lezione è stata definita la matrice N, costituita dalle tre funzioni di forma N₁, N₂ e N₃, con la quale è stato possibile legare lo spostamento lungo X ed Y di un generico punto interno all’elemento triangolare agli spostamenti nodali dello stesso.

$$ \begin{bmatrix} u(x,y))\\ v(x,y)) \end{bmatrix} = \begin{bmatrix} N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) & 0 \\ 0 & N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) \end{bmatrix} \begin{bmatrix} u_1\\ v_1 \\ u_2 \\ v_2 \\ u_3 \\ v_3 \end{bmatrix} $$

Che nel caso tridimensionale diventa:

$$ \begin{bmatrix} u(x,y))\\ v(x,y))\\ w(x,y) \end{bmatrix} = \begin{bmatrix} N_1(x,y) & 0 & 0 & N_2(x,y) & 0 & 0 & N_3(x,y) & 0 & 0 \\ 0 & N_1(x,y) & 0 & 0 & N_2(x,y) & 0 & 0 & N_3(x,y)& 0 \\ 0 & 0 & N_1(x,y)& 0 & 0 & N_2(x,y)& 0 & 0 & N_3(x,y) \\ \end{bmatrix} \begin{bmatrix} u_1 \\ v_1 \\ w_1 \\ u_2 \\ v_2 \\ w_2 \\ u_3 \\ v_3 \\ w_3 \end{bmatrix} $$

Con ω spostamento lungo l’asse Z.

Nota: è possibile considerare ulteriori gradi di libertà oltre agli spostamenti nodali, inserendo righe nel vettore δ e lo stesso numero di colonne nella matrice N.
$$ \begin{bmatrix} u(x,y))\\ v(x,y)) \end{bmatrix} = \begin{bmatrix} N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) & 0 & U_3\\ 0 & N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) & V_3 \end{bmatrix} \begin{bmatrix} u_1\\ v_1 \\ u_2 \\ v_2 \\ u_3 \\ v_3 \\ \xi \end{bmatrix} $$

Consideriamo ancora l’equilibrio dell’elemento triangolare tre nodi:



L’elemento triangolare può essere soggetto a carichi di diversa natura:

• Carico distribuito di superficie (S_x, S_y);
  
• Carico distribuito di volume (q_x, q_y);
  
• Carico distribuito di spigolo ( solitamente non considerato);
  
• Carico concentrato nodale (P_x, P_y) che nel caso bidimensionale coincide con i carichi di spigolo;
  
  

Ipotizziamo che il nostro sistema abbia comportamento lineare, ossia valgano le seguenti condizioni:

• Scalabilità degli effetti: l’uscita (output) del nostro sistema, sarà direttamente proporzionale all’ingresso applicato (input).
  
  

• Componibilità degli effetti: in presenza di più sollecitazioni la risposta complessiva del sistema può essere vista come somma delle risposte alle varie sollecitazioni prese singolarmente;
  

$ \delta = \delta P + \delta Q $

Sotto queste ipotesi è possibile applicare il Teorema dei Lavori Virtuali. Definiamo un vettore degli spostamenti virtuali δ_u con $$ \delta _\underline{u} = \begin{bmatrix} \delta u_1 \\ \delta v_1 \\ \delta u_2 \\ \delta v_2 \\ \delta u_3 \\ \delta v_3 \end{bmatrix} $$
Se il sistema è in equilibrio, per ogni δ_u, la somma dell’energia potenziale dovuta ai carichi e dell’energia potenziale elastica del sistema è nulla.

$ \delta U_f + \delta U_e = 0 $

Oppure, considerando al posto dell’energia potenziale il lavoro svolto dai carichi:

$ \delta W_f = -\delta U_f $

Nel caso tridimensionale l’energia potenziale elastica assume la seguente forma:

$$ U = \frac{1}{2} \int_{V} \begin{bmatrix} \sigma_x & \sigma_y & \sigma_z & \tau_{xy} & \tau_{xz} & \tau_{yz} \end{bmatrix}\begin{bmatrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \gamma_{xy} \\ \gamma_{xz} \\ \gamma_{yz} \end{bmatrix} dV $$

Che può essere ridotta, nel caso bidimensionale di Tensione Piana e Deformazione Piana, alla forma seguente:

$$ U = \frac{1}{2} \int_{V} \begin{bmatrix} \sigma_x & \sigma_y & \tau_{xy} \end{bmatrix}\begin{bmatrix} \varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{bmatrix} dV $$

La relazione esistente tra spostamenti virtuali e deformazioni virtuali, da essi indotte, può essere scritta come:

$ \delta \underline{u} \rightarrow \delta \underline{\varepsilon} = \underline{\underline{B}} \ \delta \underline{u} $

Dove $ \underline{\underline{L}} \ \underline{\underline{N}} = \underline{\underline{B}} $

e $$ \underline{\underline{L}} = \begin{bmatrix} \frac{\partial }{\partial x} & 0 \\ 0 & \frac{\partial }{\partial y} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} \end{bmatrix} $$

Possiamo dunque definire la variazione di energia potenziale elastica:

$ \delta U = \int_{V} \underline{\sigma}^T \delta \underline{\varepsilon} \ dV $

Con $$ \underline{\sigma}^T = \begin{bmatrix} \sigma_x & \sigma_y & \sigma_z & \tau_{xy} & \tau_{xz} & \tau_{yz} \end{bmatrix} $$ e $$ \delta \underline{\varepsilon} = \begin{bmatrix} \delta \varepsilon_x \\ \delta \varepsilon_y \\ \delta \varepsilon_z \\ \delta \gamma_{xy} \\ \delta \gamma_{xz} \\ \delta \gamma_{yz} \end{bmatrix} $$

• Lavoro concentrato ai nodi:
  
  

$ \delta W_p = P_{x1} \delta u_1 + P_{y1} \delta v_1 + P_{x2} \delta u_2 + P_{y2} \delta v_2 + P_{x3} \delta u_3 + P_{y3}\delta v_3 = \underline{P}^T \delta\underline{u} $

con $$ \underline{P}^T = \begin{bmatrix} P_{x1} & P_{y1} & P_{x2} & P_{y2} & P_{x3} & P_{y3} \end{bmatrix} $$

Dove P_x e P_y sono le componenti dei carichi nodali e δ_u e δ_v gli spostamenti virtuali nodali.

• Lavoro delle forze di superficie:
  
  

$ \delta W_s = \int_{sup} (S_x \delta u(x,y) + S_y\delta v(x,y))dS $=
$$ =\ \int_{sup} \begin{bmatrix} S_x(x,y) & S_y(x,y) \end{bmatrix}\begin{bmatrix} \delta u(x,y)\\ \delta v(x,y) \end{bmatrix} dS $$ = $ \ \int_{sup} \underline{S}^T(x,y) \underline{\underline{N}}(x,y)\delta\underline{u}dS $=$ \delta W_s = \delta\underline{u}\int_{sup} \underline{S}^T(x,y) \underline{\underline{N}}(x,y)dS $=$ \delta W_s = \underline{F}^T_s \delta\underline{u} $

In cui F_s^T sta ad indicare un vettore di forze ai nodi “energeticamente” equivalenti alle forze di superficie agenti sull’elemento. Tramite questo espediente, infatti, si è riuscito a “tradurre” dei carichi superficiali in carichi/forze ai nodi, rendendo il tutto di più facile lettura e facilitando così le successive operazioni.
Per chiarire le idee, supponiamo di avere un lato (lato 23) del nostro elemento triangolare soggetto ad un carico distribuito (di superficie) costante che scomponiamo nelle due componenti S_x ed S_y lungo gli assi. Il lato ha lunghezza l e l’elemento ha spessore t. Si può notare, andando a graficare l’andamento delle funzioni di forma N₁, N₂ e N₃ esclusivamente per il suddetto lato, che, come noto, N₂ cresce linearmente dal vertice 3 al vertice 2: essa infatti è nulla in 3 ed unitaria in 2; lo stesso per N₃: in 2 assume valore nullo mentre in 3 ha valore pari ad uno. Notare inoltre che N₁ è identicamente nulla per ogni punto del lato 23 ( N ha comportamento rettilineo lineare ed essendo N₁ nulla sia in 2 che in 3, deve per forza essere nulla anche nei punti compresi).



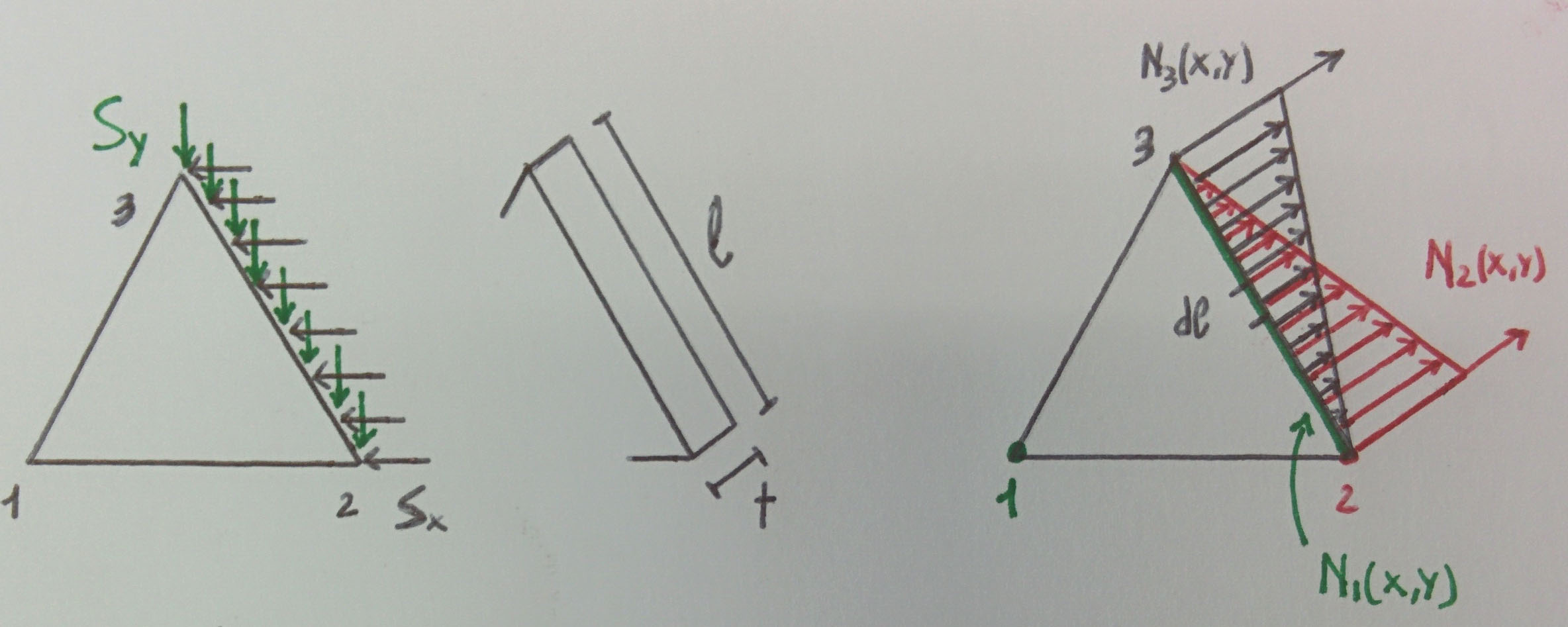
Andiamo ora a determinare il vettore F_s^T nella pratica:

$$ \underline{F}_s = \int_{sup.\bar{23}} \begin{bmatrix} S_x(x,y) & S_y(x,y) \end{bmatrix}\begin{bmatrix} N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) & 0 \\ 0 & N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) \end{bmatrix}dS_\bar{23} $$

Si può immediatamente notare che si tratta di un vettore di sei elementi, dato che deriva dal prodotto matriciale tra S^T che è una 1×2 ed N che è una 2×6: il primo elemento rappresenta la componente del carico al nodo 1 equivalente (al carico di superficie), in direzione X; il secondo la componente del carico al nodo 1 equivalente, in direzione Y; il terzo la componente del carico al nodo 2 equivalente, in direzione X e così via per gli altri tre elementi di F_s^T, fino al nodo 3. Il tutto si può facilmente osservare andando a determinare analiticamente, elemento per elemento, il vettore F_s^T.

Elemento 1: $ \underline{F}_s = \int_{sup.\bar{23}} (S_xN_1 + S_y0)dS_\bar{23} $

Elemento 2: $ \underline{F}_s = \int_{sup.\bar{23}} (S_x0 + S_yN_1)dS_\bar{23} $

Elemento 3: $ \underline{F}_s = \int_{sup.\bar{23}} (S_xN_2 + S_y0)dS_\bar{23} $ cioè $\underline{F}_s = S_x \int_{sup.\bar{23}} N_2 dS_\bar{23}$

Andando a sostituire l’integrale di N₂ sulla superficie con la media integrale di N₂ sul lato 23 che vale un mezzo e considerando dsup = t·l otteniamo:

$ \underline{F}_s = \frac{l}{2}tS_x $

Seguendo lo stesso procedimento e facendo le stesse ipotesi si ottengono in maniera analoga gli elementi 4, 5 e 6 del vettore F_s^T. In parole povere possiamo dire che un nodo si prende metà del carico distribuito (sotto forma di carico nodale) mentre l’altro si prende l’altra metà del carico, a lui più vicino.







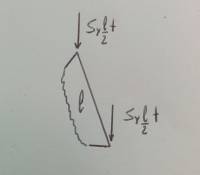
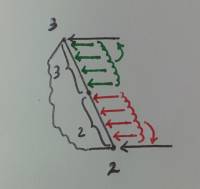
Prendiamo ora come esempio un carico superficiale distribuito in maniera non uniforme (ad esempio una tipica distribuzione a farfalla dovuta a sollecitazione flettente): per note proprietà geometriche le risultanti dei carichi, aventi modulo pari a P·l/2·t·1/2, si troveranno a 2·l/3 dal punto in cui il carico risulta nullo, come può notarsi dalla figura:



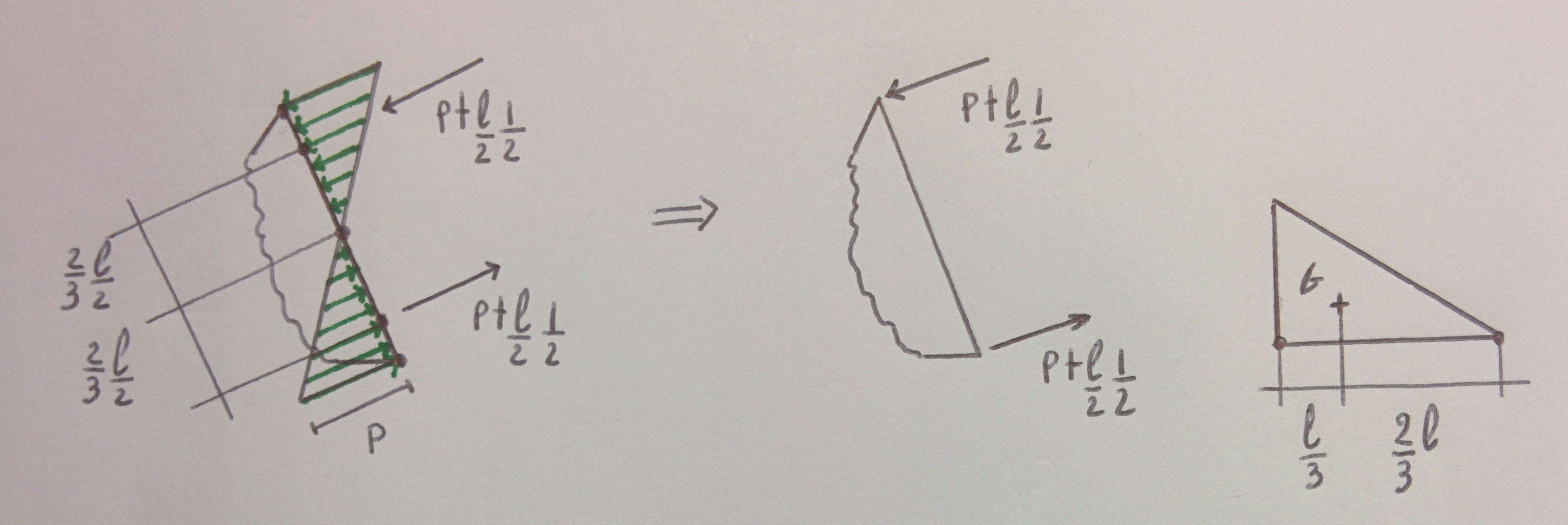
L’equivalenza nodale nel caso di carichi superficiali non uniformi non vale: infatti, osservando la figura, si vede che “traducendo” il carico distribuito in carico nodale, si incorre in una parziale sovrastima dei momenti, andando con questa operazione a variare i bracci delle risultanti.

• Lavoro delle forze di volume:
  
  

$\delta W_{vol} = \int_{Vol.} (q_x(x,y) \delta u(x,y)+q_y(x,y) \delta v(x,y))dV$=
$$\ \int_{Vol.} \begin{bmatrix} q_x(x,y) & q_y(x,y) \end{bmatrix}\begin{bmatrix} \delta u \\ \delta v \end{bmatrix}dV$$

In maniera analoga al caso superficiale precedente, considerando il vettore degli spostamenti infinitesimi come prodotto tra la matrice N ed il vettore δ_u e portando fuori quest’ultimo dall’operatore integrale (essendo un vettore costante), otteniamo rispettivamente:

$$\delta W_{vol} = \int_{Vol.} (\begin{bmatrix} q_x(x,y) & q_y(x,y) \end{bmatrix}\underline{\underline{N}}(x,y) \delta \underline{u})dV$$ = $$\ \delta \underline{u} \int_{Vol.} (\begin{bmatrix} q_x(x,y) & q_y (x,y) \end{bmatrix}\underline{\underline{N}}(x,y) )dV$$

=$ \ \underline{F}^T_v \delta\underline{u} $

Otterremmo dunque un vettore F_vol^T anch’esso di sei elementi.
Per esempio: