Indice
WORK IN PROGRESS
1 - MODI VIBRAZIONALI DI STRUTTURE SIMMETRICHE
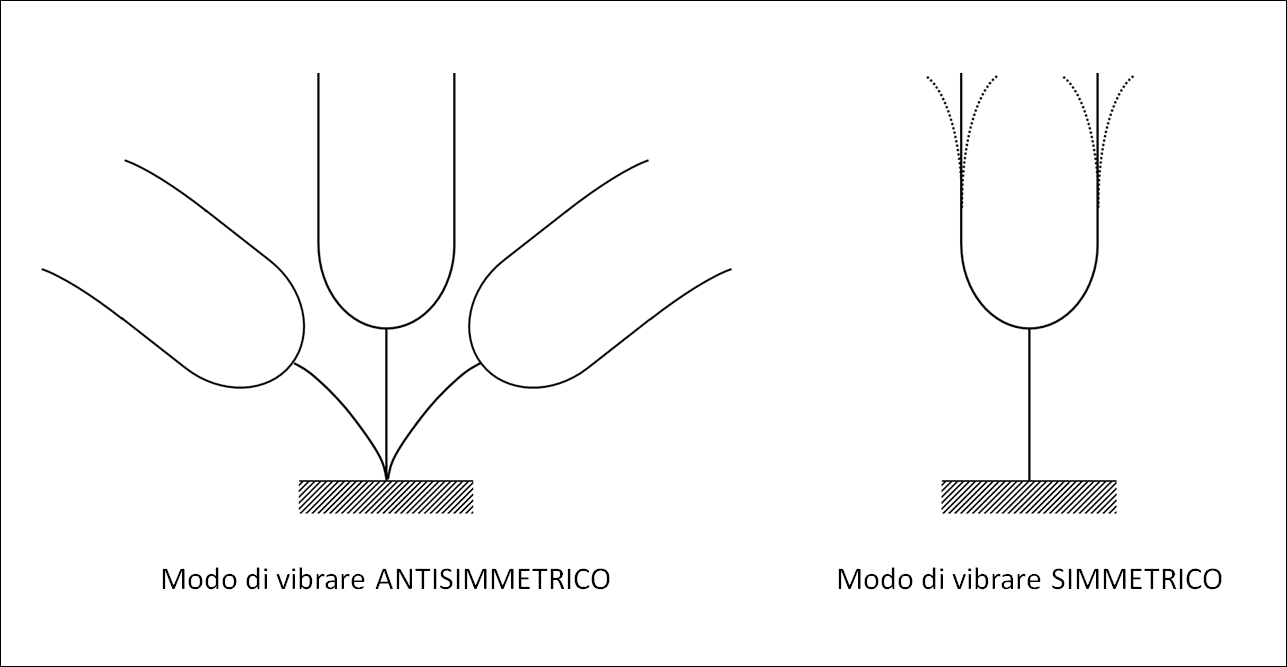
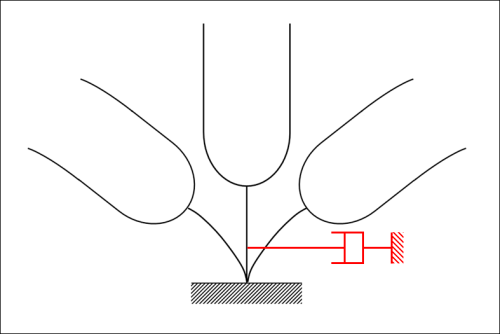
Per una struttura in cui esiste una simmetria geometrica, di massa, di materiale (modulo di Young – E) e di vincolamento, i modi propri di vibrare possono essere esclusivamente simmetrici e antisimmetrici. Considerando l’esempio di una struttura simmetrica a forma di diapason è possibile estrapolare facilmente (come in figura 1) due modi di vibrare: uno simmetrico e uno antisimmetrico
Si considera la struttura del diapason e si modella sfruttando la simmetria geometrica. Nel momento in cui occorre vincolare la struttura si può scegliere tra effettuare un vincolamento simmetrico o antisimmetrico. Tramite un vincolamento simmetrico si otterranno come risposta solamente le forme modali simmetriche, mentre con un vincolamento asimmetrico quelle antisimmetriche. È dunque necessario considerare la totalità delle soluzioni analizzando entrambi i casi con le diverse modalità di vincolamento.
1.1 - IL CASO 2D DEL DIAPASON
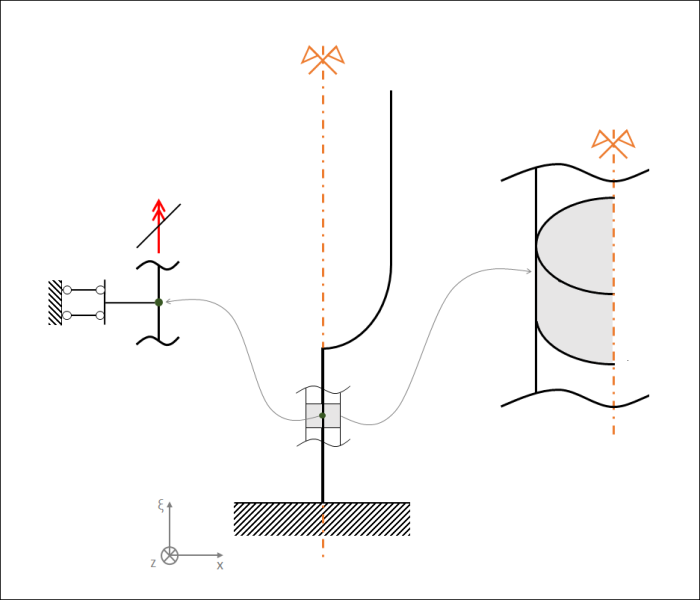
La simmetria semplifica la modellazione del diapason. Tuttavia occorre aggiungere degli opportuni vincoli di simmetria negli elementi che giacciono lungo il piano di simmetria poiché lo stelo (modellato con una fila di elementi cilindri assialsimmetrici) fa insorgere il problema di vincolare tale elemento di tipo trave. Generalmente si vuole posizionare un doppio pendolo 1)). Poiché lo stelo è modellato come elemento trave avente un’unica file di elementi lungo il proprio asse, siamo costretti a dividere in due tali elementi. In questo modo una metà può essere correttamente vincolata ma, inevitabilmente la struttura di mesh si complica.
Affinché la simmetria venga rispettata vengono introdotti negli elementi semi cilindrici i seguenti vincoli ai nodi: rotazione intorno agli assi X, Y e Z nulli e gli spostamenti perpendicolari al piano di simmetria nulli.
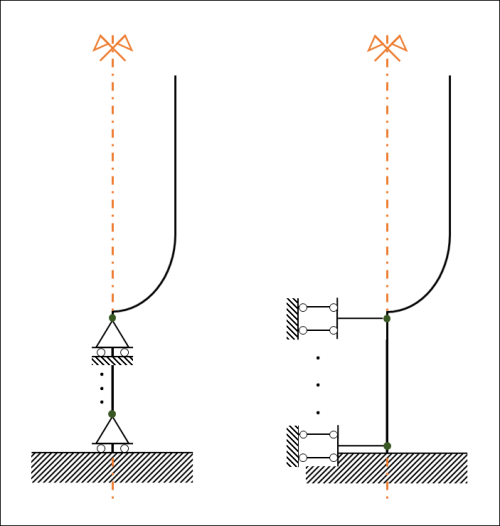
Occorre dire che tale possibilità è limitata a questo caso specifico (diapason) dove i vincoli assorbono le diversità tra il nuovo e il vecchio modello. Si veda, ad esempio, come una forza normale applicata al baricentro dello stelo provoca nel nuovo modello una curvatura sulla sezione dell’elemento dimezzato ma, grazie al vincolamento, tale deformazione viene correttamente negata. Se si lavora in campo elastico si può inoltre ipotizzare un nuovo tipo di modellazione del tutto equivalente (che sfrutta ancora la simmetria della struttura). Si costruisce un elemento cilindrico assialsimmetrico con proprietà di materiale dimezzato (densità ρ e modulo di Young E). in questo modo l’operazione di ricostruzione della geometria permette di riottenere la struttura corretta. Una volta vincolata correttamente la struttura nei due casi (simmetrico e antisimmetrico) è possibile ottenere il numero corretto di soluzioni dall'analisi modale combinando i casi.
N.B. Nel caso in cui la struttura possiede più piani di simmetria è necessario considerare tutte le possibili combinazioni di vincolamento simmetriche (s) e antisimmetriche (a) tra i tre piani. (le combinazioni possibili sono 8: a-a-a, a-s-a, a-a-s, s-a-a, s-s-a, s-a-s, s-s-s, a-s-s).
2 - ANALISI MODALE DI UNA STRUTTURA ECCITATA DA UNA FORZANTE DI PULSAZIONE PROPRIA DEL MOTO LIBERO
Il sistema di equazioni differenziali del moto è:
$\underline{M}\ddot{\overline{x}}+\underline{C}\dot{\overline{x}}+\underline{K}\overline{x}=\overline{F}(t) \qquad(1)$
Se la forzante è del tipo:
$\overline{F}(t)= \overline{f}e^{j\omega _{i}t} \qquad(2)$
Con $\omega _{i}$ pari ad una pulsazione propria del moto libero del sistema non smorzato, allora esistono soluzione del tipo:
$ \overline{x_{i}}(t)=Q_{i}\overline{x_{i}}e^{jw_{i}t} \qquad(3)$
Derivando la (3) si ottiene:
$\dot{x_{i}}(t)=Q_{i}Jw_{i} \overline{x_{i}}e^{jw_{i}t}$ $$\qquad(4)$$ $\ddot{x_{i}}(t)=Q_{i}Jw_{i}^{2} \overline{x_{i}}e^{jw_{i}t}$
E sostituendo nella (1) si ottiene:
$-a_{i}\omega_{i}^{2}e^{j\omega _{i}t} \underline{M}\overline{x_{i}}+a_{i}j\omega _{i}\underline{C}\overline{x_{i}}e^{j\omega _{i}t}+a_{i}\underline{K}\overline{x_{i}}e^{j\omega _{i}t}=\overline{f}e^{j\omega _{i}t}$ $$\qquad(5)$$ $a_{i}(\underline{K}-\omega _{i}^{2}\underline{M})\overline{x_{i}}+a_{i} jw_{i}\underline{C}\overline{x_{i}}=\overline{f}$
Poiché $\omega _{i}$ è una pulsazione propria del sistema non smorzato si ha che:
$(\underline{K}-\omega _{i}^{2}\underline{M})=\overline{0 } \qquad(6)$
e di conseguenza:
$a_{i}j\omega _{i}\underline{C}x_{i}=\overline{f} \qquad(7)$
Ovvero, le forza esterne possono essere bilanciate solo dal contributo dello smorzamento.
Premoltiplicando ambo i membri per un $\overline{x_{i}^{T}}$ è possibile ricavare il coefficiente $a_{i}$:
$\frac{\overline{x_{i}^{t}}\overline{f}}{j\omega _{i}\overline{x_{i}^{T}}\underline{C}\overline{x_{i}}} \qquad(8)$
Si nota come il coefficiente $a_{i}$ sia nullo indipendentemente dallo smorzamento se:
- $\overline{f}$ e $\overline{x_{i}}$ sono del tipo:
$$\overline{f}=\begin{pmatrix} 0\\ 0\\ \vdots \\ f_{j}=0\\ 0\\ \vdots \\ 0 \end{pmatrix} ; \overline{x_{i}}=\begin{pmatrix} \neq 0\\ \neq 0\\ \vdots \\ x_{i,j}=0\\ \neq 0\\ \vdots \\ \neq 0 \end{pmatrix} \qquad(9)$$
- $\overline{f}=\overline{x_{i}}=0\qquad(10)$
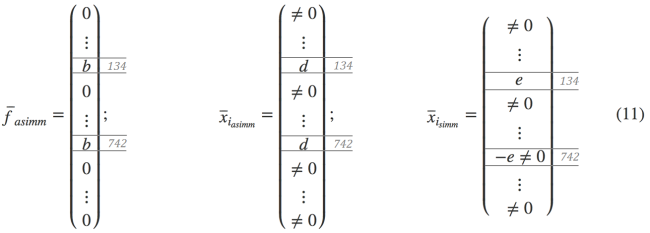
Esempio con
$\overline{f}=\overline{x_{i}}=0$ :
$\overline{f}_{asimm}\cdot \overline{x}_{i_{asimm}}=2bd \qquad(12)$
$\overline{f}_{asimm}\cdot \overline{x}_{i_{simm}}=0 \qquad(13)$
allora si hanno ampiezze nulle per i termini simmetrici di $\overline{\xi }$ e antisimmetrici di $\overline{f} $ o analogamente per:
$\overline{f}_{simm}\cdot \overline{x}_{i_{simm}}=0 \qquad(14)$
Se invece si ha un denominatore $\overline{x}_{i}^{T}\cdot \overline{f}\neq 0 \qquad(15)$
e uno smorzamento molto piccolo o nullo, si possono ottenere forme modali con enormi ampiezze. Ciò generalmente può accadere anche se $\underline{C}$ ha termini molto grandi come nel caso in cui lo smorzatore è applicato su elementi che, secondo il moto considerato, sono immobili.
$$\overline{C}=\begin{pmatrix}& \vdots & \\ \dots & c_{i,j}&\dots \\ & \vdots & \end{pmatrix} ; \overline{x_{i}}=\begin{pmatrix} x_{i1}\\ \vdots \\ x_{ij}=0\\ \vdots \\ x_{in} \end{pmatrix} \qquad(16)$$
3 - ANALISI DI RISPOSTA DIRETTA
L’analisi modale si riduce nel caso generale a risolvere la (17):
$(-\omega _{i}^{2}\underline{M}+j\omega _{i}\underline{C}+\underline{K})\overline{x}=\overline{f} \qquad(17)$
Dove si può porre (non è necessario):
$\underline{C}=\alpha \underline{M}+\beta \underline{K} \qquad(18)$
Il calcolo è effettuato per una determinata omega della forzante $\overline{f}$.
3.1 - ANALISI DI RISPOSTA PER SOVRAPPOSIZIONE MODALE
vedi anche dispensina ebertocchi
Sono valide le condizioni di ortogonalità per le forme modali:
$$\left\{\begin{matrix} \overline{x}_{j}^{T}\underline{M}\overline{x_{i}}=\delta _{ij}\\ \overline{x}_{j}^{T}\underline{K}\overline{x_{i}}=\delta _{ij}\omega _{i}^{2} \end{matrix}\right. \qquad(19)$$
Una struttura con n gdl ha n modi e frequenze proprie; tipicamente non vengono considerate tutte, e in particolare vengono trascurate quelle a frequenza propria maggiore (ndEB).
In base a valutazioni ingegneristiche da discutersi vengono prese in considerazione solo le prime m forme modali (quelle a frequenza propria più prossima alle frequenze di modulazione della forzante, e quindi più significative in quanto potenzialmente risonanti) in modo da esprimere la risposta come combinazione lineare di queste:
$\overline{x}=\overline{x_{1}}\overline{\zeta _{1}}+\overline{x_{2}}\overline{\zeta _{2}}+…+\overline{x_{m}}\overline{\zeta _{m}} \qquad(20) $
Si nota che tali combinazioni non coprono l'intero spazio $R^n$ delle configurazioni deformate possibili con n gdl., ma solo un sottospazio accuratamente selezionato. (ndEB)
Si definisce la matrice modale utilizzando gli autovettori $x_1 \ldots x_m$ come colonne
$ \underline{X}=\left [ \overline{x_{1}},…,\overline{x_{m}} \right ] \qquad(21) $
Si ottiene quindi una forma compatta della combinazione lineare di cui sopra
$\overline{x}=\underline{X}\overline{\xi } \qquad(22) $
Sostituendo tale relazione all'equazione del moto (17), premoltiplicando la stessa per $\underline{X}^{T}$ e riducendo la matrice di smorzamento C alla forma proporzionale di Rayleight si ottiene:
$\underline{X}^{T}(-\omega ^{2}\underline{M}+j\omega (\alpha \underline{M}+\beta \underline{K})+\underline{K})\overline{X\xi }=\overline{X}^{T}\overline{f} \qquad(23) $
Tale formula rappresenta un sistema lineare di $m$ equazioni in $m$ incognite $\overline{\xi}$, con termine noto $\underline{\bar{q}}=\underline{\underline{X}}^{T}\underline{\bar{f}}$
dove la matrice di sistema
$ \underline{\underline{X}}^{T} \left( -\omega^{2}\underline{\underline{M}} +j\omega (\alpha \underline{\underline{M}}+\beta \underline{\underline{K}}) +\underline{\underline{K}} \right) \underline{\underline{X}} \qquad(24) $
è diagonale essendo
$ \underline{\underline{X}}^{T} \underline{\underline{M}} \underline{\underline{X}} = \underline{\underline{I}} \qquad(25) $
con $\underline{\underline{I}}$ matrice identità e
$$ \underline{\underline{X}}^{T} \underline{\underline{K}} \underline{\underline{X}} = \begin{pmatrix} \omega _{1}^{2} & & \\ & \ddots & \\ & & \omega _{m}^{} \end{pmatrix} \qquad(26) $$
in conseguenza delle condizioni di ortogonalità citate ad inizio paragrafo.
Se il sistema lineare ha matrice diagonale le equazioni risultano indipendenti nel senso che ognuna concorre da sola nel definire il valore di una specifica incognita (es. l'equazione 1 definisce $\hat{\xi}_1$, l'equazione 2 definisce $\hat{\xi}_2$ ecc.); le equazioni possono essere trattate quindi separatamente.
Consideriamo l'equazione i-esima che risulta nella forma… 
N.B.: Quanto errore si commette utilizzando una $\underline{C}$ alla Rayleigh?
In strutture complesse prive di elementi smorzanti calibrati $\underline{C}$ è definita solo in forma sommaria e non tipicamente un approccio alla Rayleigh a introdurre la quota più rilevante di approssimazione.
La valutazione dello smorzamento proprio di una struttura si basa, infatti, su pochi valori scalari ottenuti da prove sperimentali su componenti spesso solo similari, o da normative non sempre specifiche per i casi da esaminare.
I dati disponibili sono usualmente insufficienti a definire in forma completa e con precisione la matrice C.
Generalmente da letteratura o da test sperimentali possiamo ricavare una valutazione del coefficiente di smorzamento adimensionale (o frazione del critico) $\zeta _{i}$.
Tale fattore è correlato ai coefficienti $\alpha$ e $\beta$ dello smorzamento secondo Rayleigh dalla forma:
$\zeta _{i}=\frac{1}{2}\left ( \frac{\alpha }{\omega _{i}}+\beta \omega _{i} \right ) \qquad(29) $
Questa espressione tuttavia risulta sottoderminata nel definire tali coefficienti; è infatti possibile ottenere un dato $\zeta_i$ operando solo su $\alpha$, solo su $\beta$, o utilizzando una combinazione dei due.
Valutiamo empiricamente due i due casi limite.
Caso $\alpha=0$, $\beta\neq 0$.
Ho
$$\left\{\begin{matrix} \frac{\alpha }{\omega _{i}}=0\\ \zeta_{i} =\frac{1}{2}\beta \omega _{i} \end{matrix}\right. \qquad(30) $$
In questo caso lo smorzamento sia principalmente riconducibile ad una non perfetta elasticità della struttura - tipico esempio lo smorzamento strutturale. Invertendo la relazione precedente ho
$$\left\{\begin{matrix} \beta \omega _{i}=0\\ \zeta_{i} =\frac{1}{2}\frac{\alpha }{\omega _{i}} \end{matrix}\right. \qquad(31) $$
Essendo $\underline{\underline{C}}= \beta \underline{\underline{K}}$, si osserva che in questa condizione ove nella struttura vi è deformazione elastica, vi è dissipazione per fenomeni viscosi. In particolare non si ha smorzamento associato a moti di corpo rigido o a moti cinematici interni. Gli elementi smorzanti indotti da questa modellazione sono collegati in modo da far ponte tra nodo e nodo della struttura.
Caso $\alpha\neq 0$, $\beta = 0$.
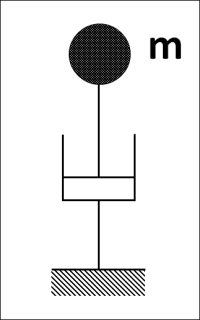
Essendo $\underline{\underline{C}}= \alpha \underline{\underline{M}}$, lo smorzamento è legato all'inerzia della struttura, ossia ove vi è accumulo di energia cinetica, ivi ho dissipazione per fenomeni viscosi. Risulta quindi che vi è dissipazione di energia associata a moti di corpo rigido o a meccanismi interni; tale comportamento è razionalizzabile immaginando degli elementi smorzanti che siano ponte tra gli elementi massivi della struttura ed un riferimento fisso (punti collegati “a terra”).
Un approccio alla Rayleigh è da evitare se sono presenti nel sistema elementi smorzanti calibrati con collegamento punto-punto tra nodi della struttura; tali elementi contribuiscono alla matrice $\underline{C}$ con un numero ridotto di termini non nulli, rispetto ai quali i termini distribuiti legati ad esempio allo smorzamento strutturale risultano trascurabili.
Ad esempio, la matrice di smorzamento relativa ad uno smorzatore concentrato $c$ inserito a ponte tra due gradi di libertà del sistema appare nella forma
$$ \underline{\underline{C}}= \begin{pmatrix} \ddots & & & \cdots & 0 \\ & c & & -c & \vdots\\ & & \ddots & & \\ \vdots & -c & & c & \\ 0 & \cdots & & & \ddots \end{pmatrix} $$
ove i termini non esplicitati risultano nulli.
Tale matrice è rappresentabile solo con grossolana approssimazione come combinazione lineare di due matrici massa e rigidezza i cui termini non nulli (= di valore non trascurabile) risultano distribuiti quantomeno su tutta la diagonale, e comunque sparsi su tutta l'estensione della matrice.



Discussione
REVISORE 1:
Sono presenti passaggi/formule/immagini che non rispettano le regole di composizione? La fruibilità del testo ne risente? Indicare puntualmente le correzioni richieste.
Sembrano rispettate nel complessivo le regole di composizione. Si potrebbe ridimensionare e posizionare meglio la figura 1. Si potrebbero al massimo inserire i sistemi di riferimento nelle seguenti figure : fig 1, fig 2 , fig 4,fig 5 e fig 6. Le formule sono corrette e scritte con la giusta formattazione del wiki.
Il testo proposto è coerente con gli appunti personali del revisore?
Il testo è abbastanza coerente agli appunti presi in aula dal sottoscritto. Inoltre è abbastanza chiaro e lineare. C'è qualche errore di scrittura da correggere ma nel complessivo va bene.
Indicare se l'aggiunta di una o più figure agevolerebbe la fruibilità del testo.
Le figure presenti vanno già bene.
Riuscirebbe uno studente che non ha seguito la lezione a preparare gli argomenti trattati sulla base di questi appunti? Quali modifiche renderebbero gli appunti più fruibili?
La lezione dovrebbe essere comprensibile anche da uno studente non presente a lezione. Infatti i passaggi da una formula all'altra sono descritti bene e la stesura della lezione è chiara.
Segnalare se si ritiene necessario un intervento diretto del docente, ad esempio nel chiarire un qualche passaggio della trattazione.
No non sono necessarie aggiunte.
Varie ed eventuali.
Nessuna
Ore dedicate a questa revisione
1/2 ora.
ndEB
La parte di trattazione ANALISI DI RISPOSTA PER SOVRAPPOSIZIONE MODALE è da integrarsi con la mia dispensa sulla dinamica linkata a inizio pagina.