====== Dinamica delle strutture elastiche discretizzata agli elementi finiti (FEM) ======
Dal punto di vista statico, la struttura è caratterizzata dalla matrice rigidezza, invece, dal punto di vista dinamico è necessario definire delle reazioni inerziali e più implicitamente definire una massa per i vari gradi di libertà che viene rappresentata adeguatamente dalla matrice massa M. Questa matrice di massa M è una matrice quadrata, avente numeri di righe e di colonne pari al numero dei gradi di libertà del sistema. Nel caso in cui avessimo gradi di libertà di traslazione la massa è una massa propriamente detta, nel caso avessimo delle rotazione la massa associata a gradi di libertà di rotazione in realtà è un momento d'inerzia. Possiamo definire la matrice massa partendo dall'energia cinetica, a sua volta definiamo l'energia cinetica prendendo un elemento finito a vari gradi di libertà, in particolare “n” gdl, l'elemento isoparametrico 4 nodi e il piano sono gli 8 spostamenti dei nodi. (Ad esempio per un elemento piastra quadrilatero 4 nodi i gdl sono 24 perchè ci sono anche le rotazioni). Per ognuno di questi gradi di libertà ho una funzione di forma, in questo caso ho “n” funzioni di forma base gdl, (solitamente le funzioni di forma sono associate al nodo più che al grado di libertà del nodo, in questo caso assoceremo le funzioni di forma al gdl). Le funzioni di forma sono definite su sistema locale $(\xi,\eta,\zeta)$, in cui è stata inserita la terza coordinata $\zeta$, poiché la matrice massa può essere definita anche per oggetti tridimensionali. Dalla versione tridimensionale delle funzioni di forma posso passare facilmente alla versione piana. In generale definisco funzione di forma relativo al gdl j-esimo un vettore
$$ \newcommand{\vec}[1]{\smash{\underline{#1}}} \newcommand{\mat}[1]{\smash{\underline{\underline{#1}}}} $$ $$ N_{j} = \begin{bmatrix} N^x_{j}(\xi,\eta,\zeta)\\ N^y_{j}(\xi,\eta,\zeta)\\ N^z_{j}(\xi,\eta,\zeta)\\ \end{bmatrix} $$
Prendo un elemento trave a due nodi, consideriamo il gdl di libertà di rotazione del nodo, con rotazione unitaria di 1rad, quindi sto considerando il gdl $(\theta_1)$.
Una volta definito il gdl $\theta_1$ posso costruire la sua funzione di forma associata in cui $\theta_1$ è il terzo secondo il nostro ordninamento, allora costruisco un vettore di 3 elementi in cui ho gli spostamenti lungo x (u), lungo y (v) e lungo z (w). Lo spostamento di un punto qualunque entro il volume, per la variazione della sola $\theta_1$ , quindi $\theta_1=1$ e tutti gli altri uguali a zero, è uguale alla funzione di forma associata a $\theta_1$ per il valore di $\theta_1$. Voglio costruire funzioni di forma in modo che preso un gdl alla volta, le funzioni di forma associate a quel gdl, devono darmi il moto di tutto il materiale dell'elemento in funzione dell'unico gdl che varia.
$$ \begin{bmatrix} u(\xi,\eta,\zeta)\\ v(\xi,\eta,\zeta)\\ w(\xi,\eta,\zeta)\\ \end{bmatrix} = \begin{bmatrix} N^x_{3}(\xi,\eta,\zeta)\\ N^y_{3}(\xi,\eta,\zeta)\\ N^z_{3}(\xi,\eta,\zeta)\\ \end{bmatrix} * \vartheta_{1} $$
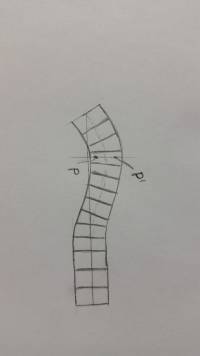
Per esempio possiamo considerare la deformazione data da una rotazione di estremità di una trave (trave 2 nodi alla Eulero, solo flessionale)
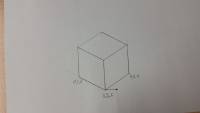
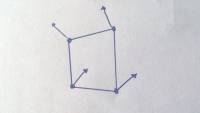
Nel disegno possiamo osservare come si configura il nostro elemento a fronte di una rotazione unitaria di $\theta_1$ . Dalla funzioni di forma e in questo caso anche dai vincoli cinematici riesco a definire come si muove ogni singolo punto della mia trave. La trave è definita su un volume in coordinate (x,y,z), in particolare, se individuo un punto P, tramite la corrispondenza biunivoca, mi posso riferire al punto in $(\xi,\eta,\zeta)$. Il punto P corrisponde ad un univoca forma di $(\xi,\eta,\zeta)$, dopodiché, secondo questa funzione di forma il punto P si va a muovere in una posizione P', muovendosi su una retta normale all'asse della trave. Quindi P diventa P', in questo caso se prendo il vettore PP' $N_3$ è la componente x del vettore PP', la seconda componente è la componente y del vettore PP', la terza componete è supposta nulla in quanto consideriamo il problema piano.Queste sono 3 funzioni che posso ricavare per ogni grado di libertà. Il senso è: la funzione di forma per gdl definisce il campo di spostamenti indotto dalla variazione di un solo grado di libertà, nelle 3 coordinate prese come vettore(in forma vettore risulta comodo tirare fuori l'energia cinetica). Se prendo per esempio un cubo
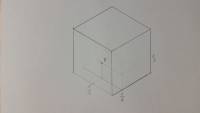
chiamo lo spostamento del nodo 4 in direzione x: $\delta_4$ . Per trovare $N^x_{4},N^y_{4},N^z_{4}$ associate al quarto grado di libertà, considero fermi tutti gli altri gradi di libertà, allora definisco la funzione di forma associata a $\delta_4$ che ha componenti nulle in y e z . Prendo un punto P che si trova come in figura
voglio trovare lo spostamento in direzione x, tramite la regola della leva applicata sui tre lati trovo lo spostamento di P in direzione x il quale vale (delta4) *3/4*2/3*1/2. Ovviamente questa relazione può essere espressa in coordinate $(\xi,\eta,\zeta)$ Se scrivo questa per un punto generico trovo la definizione di $\N^x_{4}$, quindi per ogni elemento è possibile definire come si muove un punto interno in funzione dei nodi per ogni gdl (per ogni gdl ho una funzione di forma, la funzione di forma è un modo di deformarsi del materiale interno all'elemento da scalare per quel grado di libertà, e quel modo di spostarsi lo scrivo come vettore spostamento nelle 3 componenti al posto di scriverlo come scalare indipendente)
$$ N=\frac{1} {2}(1-\xi)\frac{1} {2}(1-\eta)\frac{1} {2}(1-\zeta)=\frac{1} {8}(1-\xi)(1-\eta)(1-\zeta) $$ Che in forma di matrice relativa allo spostamento in x può essere scritta $$ \begin{bmatrix} N^x_{4}(\xi,\eta,\zeta)\\ 0\\ 0\\ \end{bmatrix} $$
Le quantità tra parentesi devono valere 1 se sostituisco il valore del nodo specifico (mi sto riferendo al nodo 4) e 0 per gli altri nodi. La funzione mi definisce la variazione lineare lungo un qualsiasi segmento del cubetto, praticamente è un estensione delle funzioni di forma dell'elemento isoparametrico 4 nodi. C'è la possibilità di definire questo vettore per ognuno dei gradi di libertà, se io considero lo spostamento associato a tutti i gdl insieme, è uguale alla somma dei singoli spostamenti dei gdl presi singolarmente. Per cui posso passare dalla sommatoria ad una notazione matriciale di un prodotto matrice vettore. Questa matrice ha tante colonne quanti sono i gradi di libertà.
$$ \begin{bmatrix} u(\xi,\eta,\zeta)\\ v(\xi,\eta,\zeta)\\ w(\xi,\eta,\zeta)\\ \end{bmatrix} = \begin{bmatrix} N^x_{1}(\xi,\eta,\zeta) N^x_{2}(\xi,\eta,\zeta) ... N^x_{n}(\xi,\eta,\zeta) \\ N^y_{1}(\xi,\eta,\zeta) N^y_{2}(\xi,\eta,\zeta) ... N^y_{n}(\xi,\eta,\zeta) \\ N^z_{1}(\xi,\eta,\zeta) N^z_{2}(\xi,\eta,\zeta) ... N^z_{n}(\xi,\eta,\zeta) \\ \end{bmatrix} \begin{bmatrix} \delta_{1} \\ \delta_{2} \\ . \\ . \\ . \\ \delta_{n} \\ \end{bmatrix} = {\mat{N}}*{\vec{\delta}} $$ Ogni spostamento di ogni punto interno al volume occupato dall'elemento in funzione degli spostamenti nodali, queste funzioni non sono variabili nel tempo percui, se faccio la derivate di esse trovo che le velocità di ogni punto interno al volume sono uguali alla matrice N moltiplicata per la derivata del vettore spostamento delta.
Se io chiamo con V il vettore velocità di tre componenti, a questo punto l'energia cinetica entro l'elemento può essere cosi scritta:
$$ E_{cin}=\int_{\Omega}\frac{1} {2}[(\frac{ \partial u }{ \partial t })^2 + (\frac{ \partial v }{ \partial t })^2 + (\frac{ \partial w }{ \partial t })^2 ]\rho d\Omega =\frac{1} {2} \int_{\Omega}( {\vec{V}^T}{\vec{V}} )\rho d\Omega $$
Essendo $$ {\vec{V}} = \underline{\underline{N}} \frac{d\delta} {dt} $$ posso scrivere:
$$ E_{cin}=\frac{1} {2}\int_{\Omega}\frac{d\delta^T} {dt}\underline{\underline{N^T}}\rho \underline{\underline{N}}\frac{d\delta} {dt} d\Omega= \frac{1} {2}\frac{d\delta^T} {dt} \int_{\Omega}\underline{\underline{N^T}}\rho\underline{\underline{N}} d\Omega\frac{d\delta} {dt}$$
Essendo N una matrice 3*n, allora la sua trasposta risulta essere una matrice n*3 e il prodotto tra di esse una matrice n*n. L'integrazione viene svolta in analogia all'integrazione della matrice rigidezza, quindi:
$$ E_{cin}=\frac{1} {2} \frac{d\delta^T} {dt} \frac{d\delta} {dt}\ [\int_{-1}^{1}\int_{-1}^{1} \int_{-1}^{1}\underline{\underline{N^T}} \rho \underline{\underline{N}} \|\underline{\underline{J(\xi,\eta,\zeta)}}| \ d\xi \ d\eta \ d\zeta] $$
A questo punto il termine compreso fra le parentesi quadre lo chiamo MATRICE MASSA e allora posso esprimere l'energia cinetica nel seguente modo:
$$ E_{cin}=\frac{1} {2} \frac{d\delta^T} {dt} \underline{\underline{M}} \frac{d\delta} {dt} $$
Se i gradi di libertà sono delle rotazioni i $$\frac{d\delta} {dt}$$ sono velocità angolari, mentre se i gdl sono altri tipi di grandezze,come per esempio la pressione idrostatica, allora i $$\frac{d\delta} {dt}$$ rappresentano la variazione nel tempo di quelle grandezze. Quindi sono da considerarsi velocità solo in senso esteso.
La matrice massa cosi ottenuta è per definizione definita positiva, mentre l'energia cinetica è da considerarsi semidefinita positiva, essendo nulla in corrispondenza di moto con velocità nodali nulle. Quindi a differenza della matrice rigidezza, per la quale ci sono moti che danno luogo a energia potenziale elastica nulla ( i moti di corpo rigido ), non esiste nessun moto che dà energia cinetica nulla. La matrice di massa per costruzione è pure simmetrica. Questo è il procedimento che permette di ricavare la matrice massa di un elemento finito qualunque, sia 2D che 3D. Abbiamo cosi trovato il legame tra tale matrice e l'energia cinetica.
Ora proviamo a trovare la relazione tra questa matrice e la legge di Newton. La variazione di energia cinetica (di elemento) nel tempo è uguale alla potenza esercitata dalle forze nodali esterne, cioè:
$$ \frac{dE_{cin}} {dt}= \frac{d\delta^T} {dt} \underline{F} $$
Ora proviamo a scriverla in funzione della matrice massa:
$$ \frac{dE_{cin}} {dt}= \frac{ \partial }{ \partial t } (\frac{1} {2} \frac{d\delta^T} {dt} \underline{\underline{M}} \frac{d\delta} {dt})= \frac{1} {2}\frac{d} {dt}\frac{d\delta^T} {dt}\underline{\underline{M}} \frac{d\delta} {dt} + \frac{d\delta} {dt}\underline{\underline{M}}\frac{d} {dt}\frac{d\delta} {dt} = \frac{1} {2} ([\frac{d} {dt}\frac{d\delta^T} {dt}\underline{\underline{M}}\frac{d\delta} {dt}]^T + \frac{d\delta} {dt}\underline{\underline{M}}\frac{d} {dt}\frac{d\delta} {dt}=\frac{d\delta^T} {dt}\underline{\underline{M}}\frac{d} {dt}\frac{d\delta} {dt}$$
Poichè questa relazione vale per ogni possibile vettore velocità deve essere:
$$ \underline{F} = \underline{\underline{M}} \frac{d^2\delta} {dt^2}$$,
cioè il vettore delle forze da applicare ai nodi per ottenere una data accelerazione deve essere uguale al prodotto della matrice massa per il vettore delle accelerazioni nodali. Questo è l'equivalente della legge di Newton e ci dà un interpretazione fisica di cos'è la matrice massa. Prendiamo il seguente elemento:
Definite delle arbitrarie accelerazioni nodali, tra le funzioni di forma viste prima definisco di conseguenza l'accelerazione di ogni punto interno all'elemento. Allora la matrice di massa è quella matrice che mi trasforma questo arbitrario stato di accelerazione nelle forze da applicare ai nodi per ottenere lo stesso, le quali sono forze uguali contrarie alla reazione inerziale del materiale dell'elemento.
Questa matrice è detta MATRICE DI MASSA CONGRUENTE. Il termine congruente sta a significare che è energeticamente congruente. Per come è costruita non è per forza diagonale. Ci sono alcune applicazioniin cui è comodo averla diagonale: si tratta dei solutori espliciti, in cui la matrice di massa è la matrice del sistema di eq. lineari e quindi averla diagonale significa avere n eq. indipendenti. In questi casi allora si utilizza una definizione di matrice di massa diversa da quella vista: si tratta della MATRICE A MASSE CONCENTRATE, o “lumped mass matrix”. E' costruita in modo leggermente diverso: si prende il volume del nostro elemento, lo si porziona in aree di influenza dei singoli nodi in modo tale che la massa di ogni area di influenza va a definire la massa nodale del relativo nodo.
$$ \underline{\underline{M}}=\begin{bmatrix} m_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & m_{1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & m_{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & m_{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & m_{3} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & m_{3} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & m_{4} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & m_{4} \\ \end{bmatrix} $$
Un difetto di questa matrice è che nei casi più complessi è necessario un algoritmo per determinarla, o comunque non è nota una procedura collaudata. Un problema pratico è che si tende a sovrastimare l'inerzia alla rotazione. Infatti se considerate il momento d'inerzia alla rotazione attorno ad un certo polo O del corpo, voi avete spostato una massa che propriamente andava collocata al baricentro dell'area in estremità all'area stessa. Quindi si aumentano i raggi d'inerzia di tutte queste masse. Per cui si va a sovrastimare l'inerzia alla rotazione. Ovviamente questo difetto è tanto più rilevante quanto la mesh è grossolana e cala al diminuire della taglia della mesh. A traslazione invece questo problema non si verifica. In caso di necessità invertire tale matrice è molto semplice, basta costruire una matrice diagonale con elementi inversi a quelli della matrice di partenza.
A questo punto possiamo scrivere l'equilibrio dinamico della struttura, in particolare di un sistema ad n gdl. Esso è dato dalla seguente equazione:
$$ \underline{\underline{M}} \frac{d^2\delta} {dt^2} + \underline{\underline{C}} \frac{d\delta} {dt} + \underline{\underline{K}} \delta = F_{est}(t) $$
dove
M è la matrice di massa, simmetrica e definita positiva; C è la matrice di smorzamento viscoso, simmetrica e semidefinita positiva; K è la matrice di rigidezza, simmetrica e semidefinita positiva: tale matrice può essere a termini complessi se si include una quota di smorzamento strutturale; F_{est}(t) è il vettore delle forza nodali applicate;
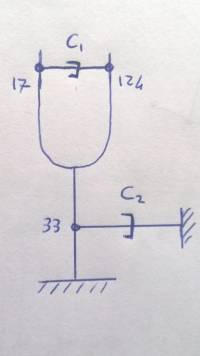
Spendiamo due parole sulla matrice di smorzamento viscoso C. In particolare proviamo a determinarla nel seguente caso:
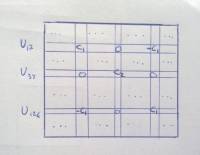
Supponiamo di avere un diapason e inseriamo uno smorzatore C1 con asse orizzontale tra i gdl spostamento lungo x di un ipotetico nodo 124 e spostamento lungo x di un altro nodo 17. Mettiamo un altro smorzatore C2 tra il nodo 33 e un collegamento a terra. In questo caso la matrice di smorzamento viscoso viene costruita assemblando i 2 smorzatori. I gdl rilevanti sono 3 e sono dati dagli spostamenti lungo x dei nodi 17, 33 e 124.
Tornando all'equazione di equilibrio dinamico possiamo notare che le incognite (delta e le sue derivate prima e seconda) sono delle funzioni e quindi non sono delle entità algebriche. Dobbiamo allora ridurre il problema in un problema algebrico sperando rimanga di interesse ingegneristico. La riduzione tipica consiste nel fare l'ipotesi di sistema lineare in modo da avere molte proprietà da sfruttare per rendere algebrico il problema e darlo in pasto ad un calcolatore per ottenere il risultato desiderato. Inoltre ci si mette in condizioni di sollecitazione periodica; è quindi possibile definire un periodo e scomporre la stessa in serie di Fourier. Per cui una volta che si la definisce periodica non è ulteriormente limitante il considerare tale sollecitazione puramente armonica e quindi modulata secondo seno o coseno. Allora scompongo il sistema nei vari contributi secondo Fourier, considero la risposta del sistema ad ogni singola componente e sotto ipotesi di linearità la risposta globale è la composizione delle risposte sulle singole componenti.
Tra le armoniche al posto di un generico $$ \underline{f(t)} $$ posso prendere $$ \underline{f}\cos(wt+φ) $$ dove $$\underline{f} $$ è un vettore perché la modulazione coinvolge forze applicate a gdl diversi. Però è più semplice considerare una sollecitazione armonica nella forma $$ F(t)=\underline{f} e^{jwt} $$ In realtà tale scrittura non è propriamente esatta, rappresenta una simbologia semplificata che fa intendere che ad essere applicata alla struttura è solo la parte reale di quel contributo. A questo punto sfruttando ancora l’ipotesi di linearità posso dire che a fronte di una sollecitazione di tipo armonico, la risposta è anch’essa di tipo armonico ed è data da:
$$ \delta(t) = \underline{x} e^{jwt} $$
In realtà lo spostamento istantaneo è la parte reale di quel contributo. La risposta periodica ad una sollecitazione periodica si può fare solo su sistemi lineari o linea rizzati nell’intorno di una posizione, dove la linearizzazione consiste in un’approssimazione.
La derivata prima nel tempo di $$ \delta(t) $$ è: $$ \frac{d\delta} {dt} = jw \underline{x} e^{jwt} $$
La derivata seconda nel tempo di $$ \delta(t) $$ è: $$ \frac{d} {dt}\frac{d\delta} {dt} = - w^2 \underline{x} e^{jwt} $$
Andando poi a sostituire le espressioni di $$ \delta(t) $$, $$ \frac{d\delta} {dt}$$, $$ \frac{d} {dt}\frac{d\delta} {dt}$$ nell’equazione di equilibrio dinamico si ottiene:
$$ - w^2 \underline{x} \underline{\underline{M}} e^{jwt} + jw \underline{\underline{C}} \underline{x}e^{jwt} + \underline{\underline{K}} \underline{x}e^{jwt} = \underline{f} e^{jwt} $$
Poiché tale equazione deve valere per ogni istante di tempo posso considerare in generale e^jwt diverso da 0 e quindi posso semplificarlo.
$$ (- w^2 \underline{\underline{M}} + jw \underline{\underline{C}} + \underline{\underline{K}}) \underline{x} = \underline{f}$$
La matrice di sistema è definita in maniera dominante dalla matrice K alle basse frequenze di sollecitazione e dalla matrice M alle alte frequenze. L’equazione trovata rappresenta un sistema di n equazioni algebriche in n incognite di tipo complesso che equivale ad un sistema di 2n equazione in 2n incognite reali una volta scorporata ogni equazione nelle sue componenti reali e immaginarie. Allora dati n gdl del sistema ottengo una forma algebrica che viene determinata risolvendo un sistema di 2n equazioni in 2n incognite reali. Quindi il peso computazionale di un calcolo di risposta dinamica periodica a sollecitazione periodica per una singola frequenza di eccitazione è pari alla soluzione statica di un sistema con il doppio dei gdl. Ricapitolando: se si ha una sollecitazione periodica, la scompongo in un numero alto quanto basta di termini in serie di Fourier, risolvo quel sistema per ogni w multiplo di w0 con quest’ultimo che è legato al periodo della sollecitazione e infine compongo i risultati. Se voglio campionare la risposta della struttura ad una sollecitazione periodica che varia di frequenza entro un certo range, allora posso definire in quel range un numero di campionamenti e per ognuno di essi risolvo il sistema. Se le matrici M,C e K o il temine noto variano in funzione della frequenza non si ha un problema aggiuntivo perché tanto per ogni frequenza nuova scrivo un sistema nuovo aggiornando le matrici o il termine noto e semplicemente lo risolvo. Per usare altre parole possiamo dire che tale legame non è un fattore che genera non linearità. Questo tipo di analisi, mediante la quale sotto opportune ipotesi si costruisce IL sistema e lo si risolve, dopodiché una volta trovato x segnato trovo gli spostamenti nel tempo e allora calcolo le tensioni, le deformazioni, le reazioni vincolari e tutte le altre grandezze agli elementi finiti, è detta ANALISI DI RISPOSTA DELLA STRUTTURA A SOLLECITAZIONE ARMONICA ECCITANTE A FREQUENZE VARIABILI.