Indice
Link di forze/momenti risultanti distributi RBE3
Gli RBE sono link, ovvero delle connessioni tra nodi della struttura in esame a nodi particolari, che godono di particolari proprietà.
Gli schemi RBE vengono utilizzati per affrontare lo studio di una struttura connessa ad un’altra senza dover completamente affrontare un’analisi FEM della seconda. Si consideri il seguente esempio. Data una piastra forata, all’interno del quale si trovi una vita o un bullone. Lo schema agli RBE permette di elaborare il modello della piastra, ponendo l'attenzione dell'indagine sulla sollecitazione e le tensioni che questa subisce per effetto dell’applicazione del serraggio della vite stessa, senza che quest’ultima sia fisicamente presente nel modello. Per ipotesi la lastra è considerata di spessore trascurabile e sia la mesh oppurtunamente discretizzata. Vado a creare quindi un nodo di controllo, che sia connesso a tutti i nodi perimetrali; ad esso si decide, ad esempio, di andare ad applicare un momento torcente.
Si propone dunque di indagare sulle leggi che regolano l’applicazione di un carico al nodo di controllo, osservando come i nodi periferici, considerati indipendenti, si comportino in questo tipo di sistema di forze.
Link RBE3
NOTA BENE: nella trattazione sottostante, la terna di assi x,y,z deve essere principale d'inerzia per la distribuzione $P_i$,$q_i$
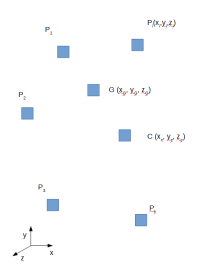
Si considera un nodo dipendete C di coordinate xC,yC, yC ,zC detto nodo di controllo (alle foze.. altrimenti la definizione è impropria) ed una nuvola di n nodi indipendenti Pi di coordinate xi,yi,zi e con peso relativo qi. Si considera applicato al nodo C un sistema di azioni esterne nella forma delle tre componenti di forza UC,VCWC e nelle tre componenti di momento ΩCΦCΨC riunite nel vettore
$\underline{F}_{C}[U_{C} V_{C} W_{C} \Omega_{C} \Phi_{C} \Psi_{C}]^T$
La simbologia utilizzata nello schema è coerente con quella utilizzata nel programma Marc.
 Si definisce un centro di massa G della nuvola di punti, le cui coordinate (riprendendo le formulazioni classiche della meccanica razionale)sono
Si definisce un centro di massa G della nuvola di punti, le cui coordinate (riprendendo le formulazioni classiche della meccanica razionale)sono
$ x_{G}= \frac{\Sigma_{i}q{i}x{i}}{\Sigma_{i}q{i}}$,$ y_{G}= \frac{\Sigma_{i}q{i}y{i}}{\Sigma_{i}q{i}}$,$ z_{G}= \frac{\Sigma_{i}q{i}z{i}}{\Sigma_{i}q{i}}$
Si definisce quindi una prima relazione di dipendenza cinematica, per cui le rototraslazioni
$\underline{\delta}_{C}= [u_{C} v_{C} w_{C} \theta_{C} \phi_{C} \psi_{C}]^T$
di C sui tre assi $x$, $y$,$z$ sono definite in funzione delle rototraslazioni
$\underline{\delta}_{G}= [u_{G} v_{G} w_{G} \theta_{G} \phi_{G} \psi_{G}]^T$
del centro di massa $G$ secondo il vincolo di rototraslazione rigida
$$ \begin{bmatrix} u_{C}\\ v_{C}\\ w_{C}\\ \theta_{C}\\ \phi_{C}\\ \psi_{C} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & +(z_{C}-z{G}) & -(y_{C}-y{G}) \\ 0 & 1 & 0 & -(z_{C}-z{G}) & 0 & +(x_{C}-x{G}) \\ 0 & 0 & 1 & +(y_{C}-y{G}) & -(x_{C}-x{G}) & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_{G}\\ v_{G}\\ w_{G}\\ \theta_{G}\\ \phi_{G}\\ \psi_{G} \end{bmatrix} $$
In questo modo si arriva ad una relazione “triangolare” dove la relazione tra il punto di controllo e i nodi indipendenti $P_{i}$ è mediata dal baricentro che funge da tramite.
Nello schema seguente si illustra la distribuzione dei momenti rispetto al sistema cartesiano e approciando i momenti nella forma “forza per braccio” più congeniale alla trattazione.
Per quanto riguarda le relazioni relative:
All'imposizione di tali relazioni cinematiche è associata una riduzione a nuovo punto di applicazione G delle azioni agenti su $C$, con l'introduzione di opportuni momenti di trasporto (vedi Teorema di Huygens) come da
$\underline{F}_{G}=[\underline{\underline{L}}_{CG}]^{T} \cdot \underline{F}_{C} $, $\underline{F}_{G}=[U_{G} V_{G} W_{G} \Theta_{G} \Phi_{G} \Psi_{G}]^T$
Si definisce quindi una seconda relazione di dipendenza per cui da una parte lo spostamento del nodo $G$ risulti la media pesata degli spostamenti ai nodi $P_{i}$, ovvero $ u_{G}= \frac{\Sigma_{i}q{i}u_{i}}{\Sigma_{i}q_{i}}$,$ v_{G}= \frac{\Sigma_{i}q_{i}v_{i}}{\Sigma_{i}q_{i}}$,$ w_{G}= \frac{\Sigma_{i}q_{i}w_{i}}{\Sigma_{i}q_{i}}$,
e dall'altra le forze applicate in $C$ e ridotte a $G$ si distribuiscano ai nodi $P_{i}$ secondo i pesi dati, ossia $ U'_{i}=U_{C} \frac{q_{i}}{\Sigma_{i}q_{i}}$,$ V'_{i}= V_{C}\frac{q_{i}}{\Sigma_{i}q{i}}$,$ W'_{i}= W_{C}\frac{q_{i}}{\Sigma_{i}q_{i}}$,
Per quanto riguarda la distribuzione dei momenti ridotti a $G$ sui nodi $P_{i}$, si preferisce operare in termini di una seconda quota di forze nodali $U''_{i}$,$V''_{i}$,$W''_{i}$ piuttosto che in termini di una quota di momenti ${\Theta}'_{i}$,${\Phi}'_{i}$,${\Psi}'_{i}$. Riferendosi alla figura precedente si considerano le componenti di momento $\Theta_{G}$,$\Phi_{G}$,$\Psi_{G}$ singolarmente nella riduzione a sistemi di forze equivalenti. Preso l'esempio particolare della componente $z$di momento $\Psi_{G}$, ad essa viene sostiutuito un sistema equivalente di forze ${\underline{F}}_{\Psi,i}$ distribuite ai punti $P_{i}$ in sole componenti $x$, $y$ tali da avere
- Retta d'azione sul piano $x$, $y$, normale alla congiungente $G-P_{i}$ qui proiettata
- verso coerente con il momento stesso
- modulo proporzionale alla distanza proiettata
$r_{z,i}=\sqrt{\Delta {x^2}_{i}+\Delta {y^2}_{i}}$, $\Delta{x}_{i}= x_{i}-x_{G}$, $\Delta{y}_{i}=y_{i}-y_{G}$ e al peso $q_{i}$ del nodo.
- momento risultante della distribuzione pari a $\Psi_{G}\widehat{k}$
In particolare risulta
$\underline{F}_{\Psi,i}=\frac{\Psi_{G}q_{i}}{\Sigma_{j}q_{j}{r^2}_{z,j}}(-\Delta{y}_{i}\widehat{\underline{i}}+\Delta{x}_{i}\widehat{\underline{j}})$
e,una volta definiti
$r_{x,i}=\sqrt{\Delta {y^2}_{i}+\Delta {z^2}_{i}}$ , $r_{y,i}=\sqrt{\Delta {z^2}_{i}+\Delta {x^2}_{i}}$, $\Delta{z}_{i}= z_{i}-z_{G}$
si hanno per le altre componanti di momento le forme
$\underline{F}_{\Theta,i}=\frac{\Theta_{G}q_{i}}{\Sigma_{j}q_{j}{r^2}_{x,j}}(-\Delta{z}_{i}\widehat{\underline{j}}+\Delta{y}_{i}\widehat{\underline{k}})$
$\underline{F}_{\Phi,i}=\frac{\Phi_{G}q_{i}}{\Sigma_{j}q_{j}{r^2}_{y,j}}(-\Delta{x}_{i}\widehat{\underline{k}}+\Delta{z}_{i}\widehat{\underline{i}})$
le quali, raccolte per componenti e in notazione più compatta, danno
$${U''}_{i}{\widehat{i}}+{V''}_{j}{\widehat{j}}+{W''}_k{\widehat{k}}=q_{i}\begin{bmatrix} \widehat{i}&\widehat{j}&\widehat{k}\\ \frac{\Theta_{G}}{\Sigma_{j}q_{j}{r^2}_{x,j}}&\frac{\Phi_{G}}{\Sigma_{j}q_{j}{r^2}_{y,j}}&\frac{\Psi_{G}}{\Sigma_{j}q_{j}{r^2}_{z,j}}\\ \Delta{x}_{i}&\Delta{y}_{i}&\Delta{z}_{i} \end{bmatrix} $$
I termini in quest'ultima equazione andranno poi sommati i contributi delle forze applicate in $C$ e ridotte a $G$ distribuite sull'i-esimo nodo $P_{i}$ . Per cui la forza distribuita dal link RBE3 sull' i-esimo nodo risulterà
$\underline{F_{i}}={U}_{i}{\widehat{i}}+{V}_{j}{\widehat{j}}+{W}_k{\widehat{k}}=({U'}_{i}+{U''}_{i}){\widehat{i}}+({V'}_{i}+{V''}_{i}){\widehat{j}}+({W'}_{i}+{W''}_{i}){\widehat{k}}$
o in forma algebrica
$$ \begin{bmatrix} U_{i}\\ V_{i}\\ W_{i}\\ \Theta_{i}\\ \Phi_{i}\\ \Psi_{i} \end{bmatrix} =q_{i} \begin{bmatrix} \frac{1}{\Sigma_{j}q_{j}} & 0 & 0 & 0 & +\frac{\Delta{z}_{i}}{\Sigma_{j}q_{j}{r^2}_{y,j}} & -\frac{\Delta{y}_{i}}{\Sigma_{j}q_{j}{r^2}_{z,j}} \\ 0 & \frac{1}{\Sigma_{j}q_{j}} & 0 & -\frac{\Delta{z}_{i}}{\Sigma_{j}q_{j}{r^2}_{x,j}} & 0 & +\frac{\Delta{x}_{i}}{\Sigma_{j}q_{j}{r^2}_{z,j}} \\ 0 & 0 & \frac{1}{\Sigma_{j}q_{j}} & +\frac{\Delta{y}_{i}}{\Sigma_{j}q_{j}{r^2}_{x,j}} & -\frac{\Delta{x}_{i}}{\Sigma_{j}q_{j}{r^2}_{y,j}} & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} U_{G}\\ V_{G}\\ W_{G}\\ \Theta_{G}\\ \Phi_{G}\\ \Psi_{G} \end{bmatrix} $$
Tale relazione è definita in forma specifica per ogni nodo $P_{i}$.
Alla distribuzione di forza appena descritta è associata la forma agli spostamenti risulta
$${\underline{\delta}}_{G}=[{\underline{\underline{L}}}_{GP,1} \cdots {\underline{\underline{L}}}_{GP,i} \cdots {\underline{\underline{L}}}_{GP,n} ] {\begin{bmatrix} {\underline{\delta}}_{1}\\ \vdots\\ {\underline{\delta}}_{i}\\ \vdots\\ {\underline{\delta}}_{n}\\ \end{bmatrix}}^{T} $$
ove ${\underline{\underline{L}}}_{GP}$ e ${\underline{\delta}}_{\forall{i}}$ sono definiti per blocchi. Ricordando la condizione cinematica per il link RBE3 si può scrivere
${\underline{\delta}}_{C} = {\underline{\underline{L}}}_{CG} \cdot {\underline{\underline{L}}}_{GP} \cdot {\underline{\delta}}_{\forall{i}}$
ed una caratteristica di distribuzione delle forze ai nodi $P_{i}$
${\underline{F}}_{i}={\underline{\underline{L}}}_{GP,i}^{T}$ $ \cdot{\underline{\underline{L}}}_{CG}^{T}$ $\cdot{\underline{L}}_{C}, i=1\dots{n}$.
Esempio
Considerare la struttura discretizzata in cui un carico $P$ allineato con uno spigolo del profilo è applicato al nodo reference di un link di carico o momento distribuito RBE3 a cui sono connessi i nodi da1 a 4 della struttura con pesi unitari Nota la modalità di distribuzione di momenti/carichi proprie dell’RBE3 definire le forze nodali che trasmette il link alla struttura.
Il primo step è la determinazione del baricentro G di coordinate ($\frac{a}{2}$;$\frac{a}{2}$). Il carico verrà distribuito su ciascun nodo equamente (P/4) .Determino i momenti di trasporto. Analizzo ogni piano ortogonale al momento di trasporto nelle 3 componenti e si otterrà:
- Nodo 1 : $\frac{P}{4}+\frac{P}{4}+\frac{P}{4}=\frac{3}{4}P$
- Nodo 2 : $\frac{P}{4}+\frac{P}{4}-\frac{P}{4}=\frac{P}{4}$
- Nodo 3 : $\frac{P}{4}-\frac{P}{4}-\frac{P}{4}=-\frac{P}{4}$
- Nodo 4 : $\frac{P}{4}-\frac{P}{4}+\frac{P}{4}=\frac{P}{4}$
immagine cinematica RBE3. 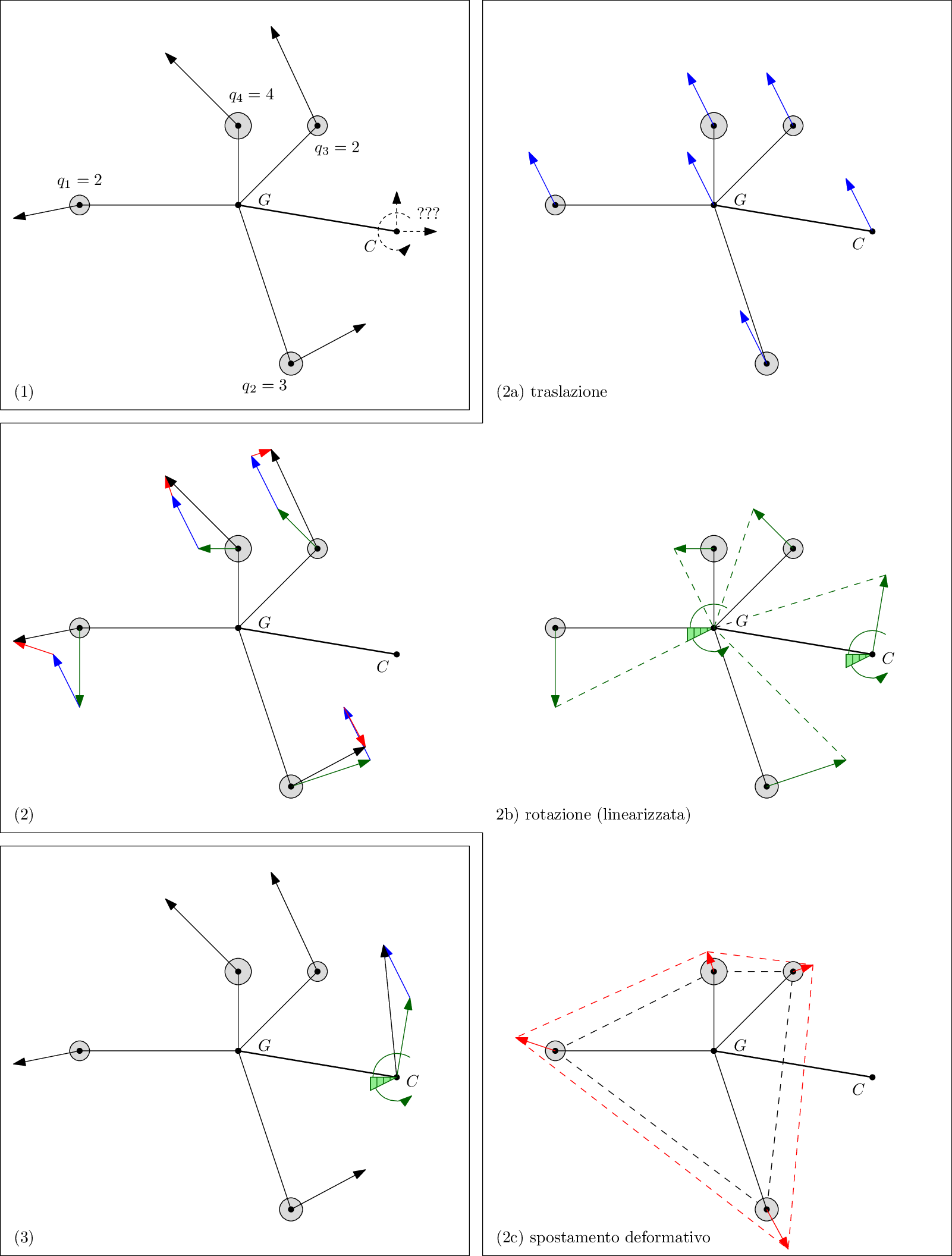 sorgente ipe
sorgente ipe
Approfondimento: analisi cinematica RBE3
Si definiscono per il sistema di punti 6 moti elementari ed i relativi versori:
- traslazione $\hat{u}$ in direzione $x$
- traslazione $\hat{v}$ in direzione $y$
- traslazione $\hat{w}$ in direzione $z$
- rotazione $\hat{\theta}$ attorno ad asse baricentrico parallelo a $x$
- rotazione $\hat{\phi}$ attorno ad asse baricentrico parallelo a $y$
- rotazione $\hat{\psi}$ attorno ad asse baricentrico parallelo a $z$
Tali versori risulteranno ortogonali. Dato quindi un generico vettore $$ \vec{\delta}=\begin{pmatrix} u_1 & v_1 & w_1 & u_2 & v_2 & w_2 & \ldots & u_i & v_i & w_i & \ldots & u_j & v_j & w_j & \ldots & u_n & v_n & w_n \end{pmatrix}^{T} $$
ottenuto accodando i vettori spostamento $\vec{\delta}_i$ dei vari nodi della distribuzione (qui $i$ e $j$ sono generici indici interi che scorrono da 1 a $n$ sui nodi), le componenti di spostamento e rotazione del baricentro saranno ottenute per proiezione di $\vec{\delta}$ sui versori associati ai moti elementari. In particolare
$u_G = \left<\vec{\delta},\hat{u}\right>_q$, $v_G = \left<\vec{\delta},\hat{v}\right>_q$, $w_G = \left<\vec{\delta},\hat{w}\right>_q$, $\theta_G= \left<\vec{\delta},\hat{\theta}\right>_q$, $\phi_G = \left<\vec{\delta},\hat{\phi}\right>_q$, $\psi_G = \left<\vec{\delta},\hat{\psi}\right>_q$
ove
$$ \left<\xi,\eta\right>_q=\sum_i q_i \xi_i \eta_i $$ indica un prodotto scalare pesato con pesi $q_i$.
Costruzione dei versori associati alle traslazioni
Consideriamo a titolo di esempio una traslazione unitaria in direzione x, nella forma $$ \vec{t}=\begin{pmatrix} \cdots & 1 & 0 & 0 & \cdots & 1 & 0 & 0 & \cdots \end{pmatrix} $$ ove sono evidenziati i contributi di due generici nodi $P_i$ e $P_j$.
Il versore $\hat{u}$ associato è costruito parallelo a $\vec{t}$, ossia
$$ \hat{u} = \lambda \vec{t} $$
con $\lambda$ tale che
$$ u_G = \left< \vec{t} , \hat{u} \right>_q = \left< \vec{t} , \lambda\vec{t} \right>_q = 1 $$
Si ottiene
$$ \lambda = \frac{1}{\left< \vec{t} , \vec{t} \right>_q} = \frac{1}{\sum_i q_i} $$
da cui
$$ \hat{u} = \frac{1}{\sum_i q_i}\begin{pmatrix} \cdots & 1 & 0 & 0 & \cdots & 1 & 0 & 0 & \cdots \end{pmatrix} $$
e, in via analoga,
$$ \hat{v} = \frac{1}{\sum_i q_i}\begin{pmatrix} \cdots & 0 & 1 & 0 & \cdots & 0 & 1 & 0 & \cdots \end{pmatrix} $$
$$ \hat{w} = \frac{1}{\sum_i q_i}\begin{pmatrix} \cdots & 0 & 0 & 1 & \cdots & 0 & 0 & 1 & \cdots \end{pmatrix} $$
Costruzione dei versori associati alle rotazioni
Si considera, in analogia con il paragrafo precedente, un moto di rotazione dei punti $P_i$ attorno all'asse baricentrico $z$ di entità pari ad un radiante.
Per semplice costruzione grafica
$$ \vec{s}=\begin{pmatrix} \cdots & -\Delta y_i & +\Delta x_i & 0 & \cdots & -\Delta y_j & +\Delta x_j & 0 & \cdots \end{pmatrix} $$ ove sono evidenziati i contributi di due generici nodi $P_i$ e $P_j$.
Il versore $\hat{\psi}$ associato è costruito parallelo a $\vec{s}$, ossia
$$ \hat{\psi} = \lambda \vec{s} $$ con $\lambda$ $$ \lambda = \frac{1}{\left< \vec{s} , \vec{s} \right>_q} = \frac{1}{\sum_i q_i \left( \Delta y_i^2 + \Delta x_i^2 + 0^2 \right)} = \frac{1}{\sum_i q_i r_{z,i}^2} $$
da cui
$$ \hat{\psi} = \frac{1}{\sum_i q_i r_{z,i}^2} \begin{pmatrix} \cdots & -\Delta y_i & +\Delta x_i & 0 & \cdots & -\Delta y_j & +\Delta x_j & 0 & \cdots \end{pmatrix} $$
e, in via analoga,
$$ \hat{\theta} = \frac{1}{\sum_i q_i r_{x,i}^2} \begin{pmatrix} \cdots & 0 & -\Delta z_i & +\Delta y_i & \cdots & 0 & -\Delta z_j & +\Delta y_j & \cdots \end{pmatrix} $$
$$ \hat{\phi} = \frac{1}{\sum_i q_i r_{y,i}^2} \begin{pmatrix} \cdots & +\Delta z_i & 0 & -\Delta x_i & \cdots & +\Delta z_j & 0 & -\Delta x_j & \cdots \end{pmatrix} $$