Le tracce B,C,D sono variate rispetto alla A per i dati numerici, per la denominazione di alcune quote simboliche (es. $l$ vs. $l/2$ vs. $l/3$) e per i versi dei carichi esterni; la procedura di soluzione proposta per la traccia A è quindi immediatamente adattabile alle altre.
Esercizio 1
Il problema delle tre forze si presenta nella sospensione motociclistica di figura prendendo in esame l'equilibrio del corpo definito dall'unione di ruota e “bielletta”.
Si nota innanzitutto che il componente “bielletta” è, come può accadere nella pratica ingegneristica e come discusso a lezione (fig. 2.40 p. 41), impropriamente denominato tale. Tale componente presenta infatti due coppie rotoidali alle estremità, ma anche un vistoso terzo punto di caricamento mediano, sul quale si inserisce la molla.
Tale corpo unione di ruota e “bielletta” riceve
- dal contatto col terreno una forza $F$ nota in retta d'azione, modulo e verso,
- dalla molla una forza nota in retta d'azione,
- dal telaio una forza nota solamente in punto di passaggio della retta d'azione.
Una volta individuati i costituenti del problema delle tre forze, si procede con la soluzione grafica indicata al par. 2.9, pag. 22; in particolare
- si ricerca il punto intersezione delle rette di azione di (1) e (2);
- per soddisfare l'equilibrio alla rotazione rispetto a tale polo, anche (3) deve avere rispetto ad esso braccio nullo; si traccia quindi la retta d'azione della forza (3) congiungendo tale punto intersezione di (1) e (2) con il punto di applicazione noto di (3).
- a parte, si ridisegna in scala a piacere il vettore forza nota (1), rispettandone orientazione e verso;
- si tracciano quindi le parallela alle rette d'azione di (2) e (3) passanti rispettivamente per la testa e per la coda (o viceversa) del vettore forza nota ridisegnato; tali parallele a (2) e (3) si incontreranno in un punto definendo un triangolo delle forze analogo a quello di fig. 2.13 a p. 22.
Esercizio 2 
NB. la cerniera mediana non interrompe la continuità della trave.
Esercizio 3
Esercizio 4
Vedasi paragrafo 2.4 p 12, con coppia C associata alle due forze 2 e 3. La risultante è una forza verticale di modulo, direzione e verso pari a quelli della forza 1, con retta d'azione scostata a destra rispetto alla forza 1 di (20N·50mm)/(100N)=10mm.
Esercizio 5
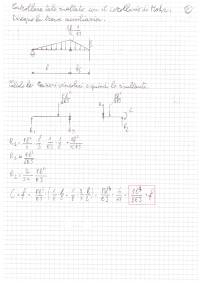
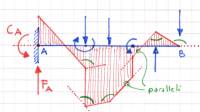
La regola del filo è trattata al par. 10.3, p.519 e sgg.. Il momento flettente si traccia a partire da B, punto in cui è nullo (estremità di trave non caricata da coppia concentrata), rispettando i cambi di pendenza e i salti propri delle azioni esterne puntualmente applicate.
Nel caso generale, taglio e momento flettente risultano in A non nulli, in quanto in generale è non nulla la risultante delle forze trasverse applicate, e non autocompensanti le azioni momento; il diagramma di $M_\mathrm{f}$ dovrebbe quindi arrivare in A con un tratto non orizzontale (ciò comporterebbe taglio nullo) e con valore in A non nullo.
Un esempio di soluzione è riportato in figura; le reazioni vincolari in A sono riportate in coerenza con l'andamento locale del momento flettente, come richiesto dal testo.
Esercizio 6
Analogo a esercizio svolto 3.9.3 a p. 100 di FCdM. Il disegno del cubetto è da svolgersi in analogia a fig. 3.41 (e).
Esercizio 7
Composizione con eventuale riorientamento delle figure 4.23(b) a p.144, 4.27(b) a p. 150 e 4.34(a) a p. 160 di FCdM.
Esercizio 8
Ci si riferisce al sistema di riferimento Oxy di figura, privo di proprietà particolari e avente l'unico pregio di non sovrapporsi ad assi e punti notevoli della sezione.
Si rammenta che il baricentro della sezione circolare forata eccentrica non coincide con il baricentro della circonferenza esterna.
Tale sezione può essere interpretata come la composizione di due figure elementari, una con contributi positivi all'area (pieno), e una con contributi negativi all'area (vuoto). Quest'ultima è caratterizzata da termini area e momento d'inerzia negativi.
Pieno (1):
$A_\mathrm{1}=\pi R^2$,
$J_\mathrm{1xx}=J_\mathrm{1yy}=\frac{\pi R^4}{4}$, con assi $1xx$ e $1yy$ baricentrici rispetto a (1),
$x_\mathrm{G1}=R$,$y_\mathrm{G1}=R$ rispetto al sistema Oxy di figura;
Vuoto (2):
$A_\mathrm{2}= -\pi r^2 < 0$,
$J_\mathrm{2xx}=J_\mathrm{2yy}= -\frac{\pi r^4}{4} < 0$, con assi $2xx$ e $2yy$ baricentrici rispetto a (2),
$x_\mathrm{G2}=R$,$y_\mathrm{G2}=R+e$ rispetto al sistema Oxy di figura.
Il baricentro della figura combinata è calcolabile come
$x_\mathrm{G}=\frac{x_\mathrm{G1} A_\mathrm{1}+x_\mathrm{G2} A_\mathrm{2}}{A_\mathrm{1}+A_\mathrm{2}}$; $y_\mathrm{G}=\frac{y_\mathrm{G1} A_\mathrm{1}+y_\mathrm{G2} A_\mathrm{2}}{A_\mathrm{1}+A_\mathrm{2}}$
I momenti d'inerzia delle due figure rispetto al baricentro della figura combinata sono
$J_\mathrm{1,Gxx}=J_\mathrm{1xx} + A_\mathrm{1} \cdot \left( y_\mathrm{G1} - y_\mathrm{G} \right)^2$;
$J_\mathrm{1,Gyy}=J_\mathrm{1yy} + A_\mathrm{1} \cdot \left( x_\mathrm{G1} - x_\mathrm{G} \right)^2$;
$J_\mathrm{2,Gxx}=J_\mathrm{2xx} + A_\mathrm{2} \cdot \left( y_\mathrm{G2} - y_\mathrm{G} \right)^2 < 0$;
$J_\mathrm{2,Gyy}=J_\mathrm{2yy} + A_\mathrm{2} \cdot \left( x_\mathrm{G2} - x_\mathrm{G} \right)^2 < 0$;
Il momento d'inerzia cumulativo si trova per somma (con segno) dei due contributi
$J_\mathrm{Gxx}=J_\mathrm{1,Gxx}+J_\mathrm{2,Gxx}$;
$J_\mathrm{Gyy}=J_\mathrm{1,Gyy}+J_\mathrm{2,Gyy}$;
Il testo non chiede di valutare i moduli di resistenza $W_\mathrm{xx}$ e $W_\mathrm{yy}$; questi sono tuttavia ricavabili dividendo i momenti d'inerzia per le massime distanze di un punto della sezione dai relativi assi neutri.
Esercizio 9
Analogo a caso di Fig. 4.42 p. 173 di FCdM, ivi risolto con formule parametriche. Essendo richiesta una tensione tangenziale nominale, non è da applicarsi il fattore di concentrazione delle tensioni di Eq. (4.80). La massima tensione tangenziale nominale appare alle pareti a spessore minore, nello specifico le verticali; il momento torcente si ricava dalla formula (4.77), con τ=70 MPa, a=10 mm, b=12 mm, t=1 mm, v=1.5 mm.
Esercizio 10
Eq. (4.20) p. 145 riporta la relazione tra momento flettente $M_f$, rigidezza flessionale $EJ$ e curvatura $\frac{1}{R}=\eta^{\prime\prime}$. Il momento d'inerzia $J$ per la sezione circolare è riportato in formula (4.17), p. 143.
Si ottiene $$ \eta^{\prime\prime} = \frac{M_f}{EJ} = \frac{64 M_f}{E \pi D^4} ; \quad D=\sqrt[4]{\frac{64 M_f}{\pi E \eta^{\prime\prime}}} $$
da cui per sostituzione numerica (E=210000 MPa, $\eta^{\prime\prime}$=0.06 $\mathrm{mm}^{-1}$) otteniamo la relazione parametrica D=0.200523$\sqrt[4]{M_f}$.
Esercizio 11
Esercizio 12
Trattazione analoga ad es. 11.3.2 a pag. 547, una volta invertito il verso della forza P e sdoppiata la stessa in due azioni P/2 e P/2 simmetricamente scostate dalla mezzeria; le considerazioni qualitative ivi discusse valgono nel caso in esame, con grafico di Mf (fig. 11.10 (i)) leggermente variato.