Es. 1
Chiamiamo O la sezione di calettamento della mola; in corrispondenza di tale sezione la mola trasmette all'albero una forza R di modulo $R=\sqrt{F^2+P^2}$, e una coppia resistente1) pari a $C_{r,O}=F \cdot r$, ove $r$ è il raggio esterno della mola. Tale coppia può essere interpretata come coppia di trasporto generata dallo spostamento della retta d'azione delle forze di taglio dall'originale posizione periferica alla mola al centro della sezione O dell'albero.
Chiamiamo $\gamma$ il piano definito da $R$ e dall'asse dell'albero.
Chiamiamo U l'estremità dell'albero accoppiata all'utilizzatore; anche in corrispondenza di tale sezione viene applicato all'albero un momento resistente $C_{r,U}$ di entità data.
Detta M l'estremità dell'albero accoppiata al motore, in corrispondenza di questa viene applicata all'albero una coppia motrice $C_{M}$ da definirsi. Risulta tuttavia che, per equilibrio alla rotazione dell'albero rispetto al suo asse (o per bilancio tra potenza entrante e uscente), $$+C_{M}-C_{r,O}-C_{r,U}=0.$$
In corrispondenza delle sezioni A e B i supporti trasmetteranno all'albero delle forze trasversali $R_A$ e $R_B$ che risulteranno allineate2) alla direzione della forza R. Il valore di tali reazioni viene valutato in $$R_A=\frac{l-a}{l}R,\quad R_B=\frac{a}{l}R$$
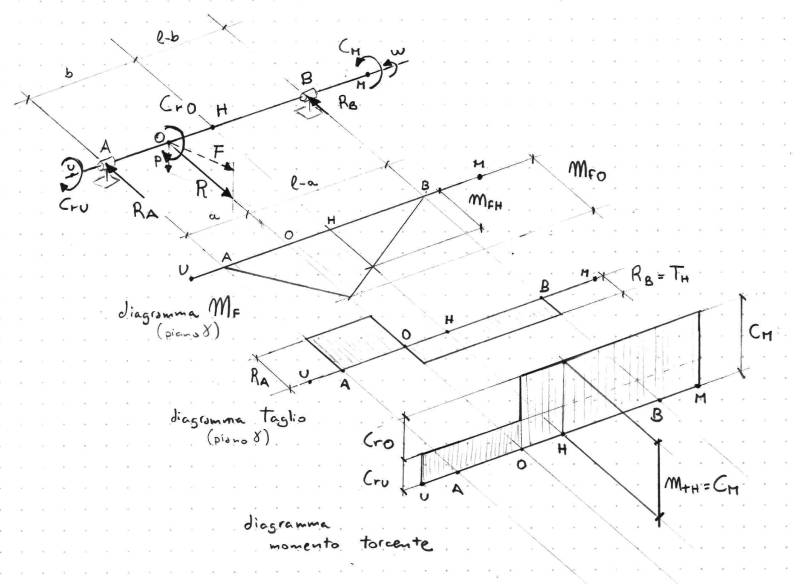
Note le azioni sull'albero, si possono derivare le caratteristiche di sollecitazione rappresentate in figura
In particolare, alla sezione H di interesse il momento flettente vale $M_{f,H}=R_B\cdot\left(l-b\right)$, il taglio vale $T_H=R_B$, e il momento torcente vale $M_{t,H}=C_M$.
Si nota in particolare che – per l'equilibrio alla rotazione rispetto all'asse del concio di albero che si estende dall'estremo U alla sezione – il momento torcente
- vale $C_{r,U}$ sui tratti UA e AO;
- è discontinuo in corrispondenza della sezione O, con un salto pari al valore $C_{r,O}$ del momento resistente applicato in corrispondenza di tale sezione;
- vale $C_{M}=C_{r,O}+C_{r,U}$ sui tratti OH, HB e BM, e sulla sezione H in particolare.
La potenza richiesta al motore è valutabile come prodotto tra coppia motrice fornita $C_{M}$ e velocità di rotazione $\omega$.
Es. 2
Oggetto dell'esercizio è il forzamento di un mozzo su di un albero pieno localmente ringrossato a creare una mazzetta, come discusso nel paragrafo 6.2.2 p. 374 e nel paragrafo 13, pp. 701-703 (cfr. Fig. 13.3 (d) p. 703).
L'interazione albero-mozzo avviene quindi su un raggio di accoppiamento $r_m=22.75$ mm pari a metà del diametro esterno della mazzetta; il raggio interno dell'albero $r_i$ è da assumersi nullo in quanto l'albero è pieno. L'estensione assiale della maschetta coincide con l'estensione assiale del contatto $l=48$ mm.
La pressione di forzamento $p_f$ necessaria a trasmettere la coppia data si ricava mediante la Eq. (11.15) p. 696; tale pressione agisce sulla superficie interna del mozzo.
La tensione ammissibile per il mozzo $\sigma_\mathrm{amm}=430\cdot 50\%=215$ MPa è valutata a partire dalla tensione di snervamento a flessione (più pertinente di quella a sforzo normale vista la presenza di un significativo gradiente tensionale al bordo interno del mozzo), reperibile a p. 250 dal diagramma di Goodman.
Posti $\Delta p = p_f$ (il mozzo non è esternamente pressurizzato) e $\sigma_\mathrm{id}=\sigma_\mathrm{amm}$ entro la (5.4) p. 673, si ottiene da questa $$r_e=r_i\sqrt{\frac{\sigma_\mathrm{amm}}{\sigma_\mathrm{amm}-2 \cdot p_f}}$$
L'interferenza diamentrale $I=2\Delta r$ è ricavabile a partire dalla (11.13) p. 694.
Le componenti radiali di tensione all'interfaccia (al raggio interno del mozzo, e al raggio esterno dell'albero) valgono $-p_f$ per continuità con la pressione di contatto.
La componente circonferenziale al raggio interno del mozzo è valutabile mediante la (3.7) p. 666, mentre nell'albero eguaglia la componente radiale, essendo un cilindro pieno soggetto ad una pressione esterna caratterizzato da uno stato tensionale idrostatico piano (vedasi Tabella 3.1 p. 668, caso $r_i=0$).
La tensione ideale nel mozzo sarebbe valutabile mediante la (5.4) p. 673, ma è per ipotesi pari alla $\sigma_\mathrm{amm}$ imposta.
La tensione ideale nell'albero viene valutata in $p_f$ applicando il criterio di Tresca ad uno stato tensionale con componenti principali $\sigma_r=\sigma_\theta=-p_f$, $\sigma_a=0$.
Es. 3
La verifica del ramo di forcella a taglio può essere svolta valutando la tensione tagliante alla sezione resistente mediante la (3.7) p. 532; la tensione tagliante critica per cicli all'origine è reperibile dal diagramma di Goodman a p. 248, e coincide con la $\tau_s$ di snervamento a torsione 3).
Le tensioni nominali per i punti A e B sono valutabili dalle Eqq. (5.2.3) p. 330 e (5.2.2) p. 329, rispettivamente, mentre i fattori di forma sono ricavabili entrando con $\frac{r_i}{r_e}=\frac{d}{w}=0.4$ in Fig. 5.2.8 p.329.
In ipotesi di $\eta\approx 1$, le tensioni teoriche coincidono con le tensioni effettive, e possono essere direttamente comparate con la tensione critica all'origine a flessione (siamo in presenza di intaglio, e quindi con gradiente tensionale significativo) per il materiale; dal sopracitato diagramma di Goodman tale tensione critica coincide con la tensione di snervamento a flessione.
La tensione tagliante sullo spinotto in corrispondenza del passaggio di portata è valutata tramite la (3.15) p. 539, mentre la pressione media di contatto (rapporto tra carico e area diametrale) coincide per la forcella con la tensione nominale propria del punto B.
Es. 4
La tensione critica a sforzo normale per carichi statici del materiale coincide con il carico di snervamento, ed valutabile in 850 MPa dal diagramma di Goodman a p. 253.
In condizioni di avviamento il fusto è sollecitato a compressione da un carico pari a quello dei gas, e dalla formula $$ P_\mathrm{scoppio} = A \cdot \frac{R_\mathrm{s}}{n} $$ con $n$ coefficiente di sicurezza, si ricava l'area resistente della sezione. Nota tale area, si ricava il valore della profondità di tasca $g$ mediante la relazione $A(g)=bh-2eg$.
L'azione dei gas è stata trattata come statica su esplicita richiesta del testo dell'esercizio; a questo primo dimensionamento segue una verifica a fatica che considererà il consueto ciclo combinato tra avviamento e regime.
Si considera quindi il ciclo di fatica con estremo trattivo pari alle forze inerziali al pms.i. ed estremo compressivo dato dalle sole azioni del gas al pms.c. in avviamento; tale ciclo viene quindi ribaltato in segno in modo da ottenerne uno equivalente a carico medio positivo; si calcola quindi il fattore $K$ per tale ciclo secondo la formula (6.1) p. 244 ottenendo $$K=\frac{1+\frac{-F_\mathrm{pms,i}}{P_\mathrm{gas}}}{2}= 0.34$$ a cui corrisponde sul diagramma di Goodman per lo sforzo normale del materiale una tensione critica di circa $\sigma_\mathrm{crit,a.a.}\approx 650 \mathrm{MPa}$.
Si procede quindi al calcolo del coeff. di sicurezza utilizzando la formula $$n=\frac{A \sigma_\mathrm{crit,a.a.}}{P_\mathrm{gas}}$$