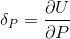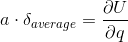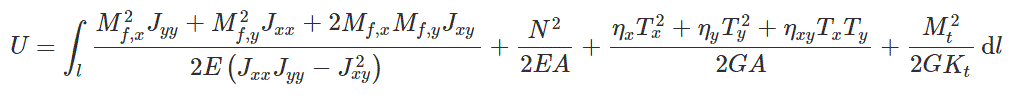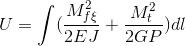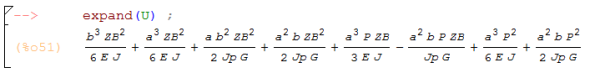STUDIO DI UN TELAIETTO CARICATO CON AUSILIO DI MAXIMA

versione cattedra, fine lezione

Maxima è un Computer Algebra System (CAS) in grado di eseguire calcoli numerici, simbolici, grafici e altre operazioni correlate. Questo software ci servirà per risolvere i sistemi di equazioni legati alle varie strutture di nostro interesse.

Aprendo l’applicazione, l’interfaccia ci appare come in figura seguente:

Il primo comando che utilizziamo all’avvio del programma è “kill(all)”, che serve a pulire la memoria cancellando i dati salvati precedentemente in altre operazioni. Dopo aver pulito la memoria, possiamo procedere con l’elencare alcune funzioni principali dell’applicazione, e la loro relativa sintassi. Innanzitutto Maxima apre automaticamente in background all’avvio un programma di calcolo con relativi dati salvati. Qualora dovessimo avere un crash dell’applicazione, possiamo dunque riavviare semplicemente questo programma in background, andando sul menù Maxima → Restart Maxima.

A questo punto possiamo inserire una cella di lavoro. Esistono due tipi di celle di lavoro: celle d’ingresso (input cells) e celle di testo (text cells). Le prime sono le celle che il programma valuta, e le utilizziamo per espressioni, equazioni, funzioni, ecc; le seconde le utilizziamo per commenti o didascalie. Possiamo inserirle dal menù Cells → Insert Input Cell / Insert Text Cell.

Tutti i nostri comandi principali, e le nostre operazioni, andranno dunque inseriti all’interno delle Input Cells. Ogni comando inserito, va confermato con Shift + Enter. Utilizzando il simbolo “;” alla fine del comando, il programma ci restituirà come risposta una soluzione, o un’impostazione particolare del problema da noi impostato. Utilizzando invece il simbolo “$” alla fine della nostra stringa, il programma eseguirà comunque il nostro comando, ma senza mostrarci il risultato svolto, utile soprattutto quando la soluzione che stiamo cercando è particolarmente lunga e va quindi ad occupare parecchie righe.

Per eseguire l’intero foglio di lavoro, con tutti i comandi impostati, possiamo usare il comando Cell → Evaluate All Visible Cells, o semplicemente premere Ctrl + R. Il programma eseguirà nuovamente tutti gli input già eseguiti in precedenza, e anche quelli ancora da eseguire, ove presenti.

Per riferirci ad un input definito nella riga precedente, invece di scriverne il nome o il numero della riga, possiamo usare il simbolo “%”

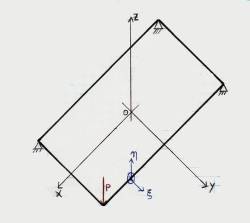
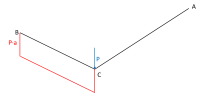
Supponiamo di avere un telaietto rettangolare, vincolato con 3 vertici appoggiati, ed il quarto caricato con una forza P agente perpendicolarmente al piano del telaietto stesso, verso il basso.

Prendiamo un sistema di assi cartesiani, centrato sul baricentro del sistema, in modo che il lato minore del telaietto sia parallelo all’asse y e quello maggiore lo sia all’asse x. Supponiamo inoltre che la nostra struttura sia costituita da tubi. Siano gli assi principali di inerzia della sezione del tubo ξ e η, consideriamo i tre momenti di inerzia $J_{ξξ}$, $J_{ηη}$, $J_{ξη}$. Nel nostro caso possiamo affermare che il terzo di questi tre termini sarà nullo, e che i primi due saranno entrambi uguali ad un certo valore J. Inoltre, definita $K_T$ la rigidezza torsionale della trave, possiamo affermare che nel caso in esame (sezione circolare cava) questa sarà uguale al momento di inerzia polare $J_P$.

Per calcolare la deformabilità normale ci servirà l’area della sezione, che ipotizziamo costante lungo ognuna delle 4 travi; per calcolare invece la deformabilità al taglio avremo bisogno anche di tre coefficienti correttivi $η_ξ$, $η_η$, $η_{ξη}$.

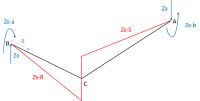
Schematizziamo il telaietto vincolato come una struttura geometricamente simile, con i quattro vertici caricati da altrettante forze verticali P, che generano un sistema di forze antisimmetrico. La struttura risulta essere 3 volte geometricamente simmetrica, ed il piano x,z è un piano di antisimmetria.

Definiamo il vincolo di simmetria come un vincolo che permette due scorrimenti lungo due assi perpendicolari, ed una rotazione intorno ad un terzo asse della terna destrorsa. Questo vincolo è cinematicamente identico ad un corpo che scorre su un piano senza staccarsi da esso. Il vincolo di antisimmetria invece permette due rotazioni attorno a due assi della terna. Questo vincolo è cinematicamente identico ad un vincolo “sfera con nasello entro cava cilindrica”.

Poiché la struttura è antisimmetrica, possiamo analizzarne solo una porzione, utilizzando questi vincoli appena descritti nei punti A e B e calcolando le reazioni vincolari.

Il nostro obiettivo è quello di calcolare, a partire dalle nostre reazioni vincolari, il cedimento $δ_C$ della struttura sotto il carico P e di confrontare questo cedimento con quello dell’intera struttura.

Impostiamo il sistema di equazioni di equilibrio (alla traslazione ed alla rotazione intorno ad O) su Maxima per ricavare le reazioni vincolari.

Per dare un nome a un’equazione o una funzione, come si nota in figura, scriviamo nella cella di input il suo nome, seguito da i due punti e dalla formula stessa (es: eqtx : XB=0, da ora in poi scrivendo “eqtx” intenderemo XB=0). Se proviamo a scrivere eqtx+1, il programma ci restituirà XB+1=0+1.

Ci troviamo davanti ad un sistema a 6 equazioni in 6 incognite, una delle quali è però nulla. Ciò comporta che il sistema è labile perché nulla impedisce la rotazione intorno all’asse z. Eliminiamo la sesta equazione, scrivendo dunque un sistema di 5 equazioni in 6 incognite, una delle quali, ZB, diventerà un parametro in funzione della quale risolveremo il suddetto sistema.

Per impostare un sistema di equazioni su Maxima, inseriamo tutte le equazioni che vogliamo dentro il sistema, separate da virgole, all’interno di due parentesi quadre (es. eqns : [eqtx, eqty, eqtz, eqrxO, eqryO] ); allo stesso modo andiamo a definire la lista delle nostre incognite (es. unks : [XB,CB,YA,ZA,CA] ).

Per risolvere un sistema di equazioni lineari utilizziamo il comando linsolve, inserendo tra parentesi le equazioni del sistema e le incognite dello stesso: linsolve(eqns,unks). Questo comando tuttavia non assegna le soluzioni trovate alle nostre incognite “unks”. Per ovviare al problema, al comando “linsolve” affianchiamo “globalsolve=true”.

Adesso possiamo procedere con l’inserimento delle funzioni “momento flettente” e “momento torcente” ricavate sulla struttura.

ATTENZIONE: nell'immagine i termini di Mf_AC sono errati in segno relativo, in particolare i contributi di P e ZB devono risultare opposti in segno, vedi lezione gruppo A

Applichiamo ora il Teorema di Castigliano per il calcolo dell’energia potenziale elastica. Tale teorema si compone di due ipotesi:

1. La struttura deve avere un comportamento lineare, ovvero deve valere la sovrapposizione degli effetti;
2. L’energia potenziale elastica è funzione delle condizioni di carico del sistema.

Consideriamo un piccolo esempio:

Analizziamo una trave incastrata, caricata con una forza F comunque orientata, con una coppia C nell’estremo libero, con un carico di punta P e con un carico q distribuito su una lunghezza a.

Lo spostamento del punto di applicazione di P (ovvero l’estremo libero della trave) sarà pari alla derivata parziale dell’energia potenziale elastica rispetto alla forza P

Analogamente ricaviamo la rotazione $θ_C$ come derivata parziale di U rispetto alla coppia C e lo spostamento del punto di applicazione del carico distribuito come derivata parziale di U rispetto a q.

L’energia potenziale elastica di una data struttura sarà data dalla formula

Consideriamo nuovamente la nostra porzione di telaietto analizzata in precedenza.

Vogliamo applicare il Teorema di Castigliano, con i momenti flettenti e torcenti ricavati su Maxima.

Per applicare i momenti ricavati al Teorema di Castigliano dobbiamo introdurre la funzione “integrate” su Maxima. Essa calcola l’integrale di una funzione integranda, con una determinata variabile, in un intervallo da noi scelto: integrate ( funzione integranda , x , a,b ).

Nel nostro caso, la U sarà somma di due contributi UBC e UAC.

Per ridurre a denominatore comune, utilizziamo la funzione fullratsimp(U).

Infine per scrivere la nostra equazione in forma monomiale utilizziamo la funzione expand(U).

Ricavato U, possiamo ora applicare Castigliano per ricavare lo spostamento del punto B in direzione z. Per applicare la formula di Castigliano dovremo inserire la funzione di derivazione diff ( U , ZB , 1 ), con l’ordine di derivazione messo come ultimo termine della parentesi. Risolviamo l’equazione col comando “linsolve” imponendo lo spostamento nullo.

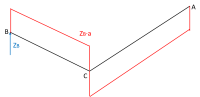
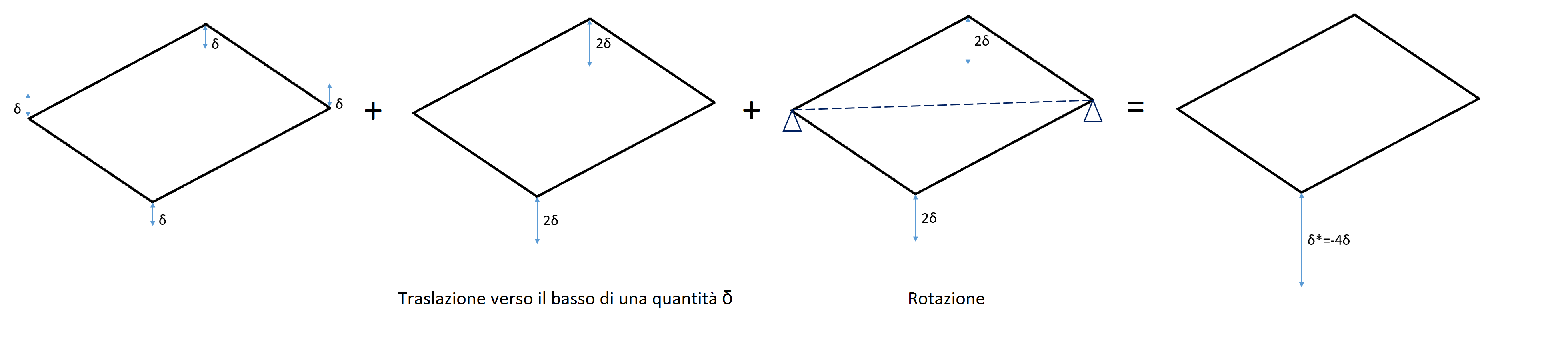
Cerchiamo la relazione tra lo spostamento $δ_C$ della nostra porzione di telaietto e quello dell'intera struttura. Le due strutture sono equivalenti dal punto di vista delle reazioni vincolari, grazie al vincolo di antisimmetria; tuttavia la stessa equivalenza non vale per gli spostamenti. La differenza tra l'intera struttura con i 4 spostamenti e quella reale potrà essere solo un moto di corpo rigido. I vertici in cui avevamo collocato i 3 appoggi (DEF) devono avere spostamento nullo, quindi, per annullare gli spostamenti di D ed F, facciamo traslare la struttura verso il basso di una quantità pari a $δ$. Non abbiamo ancora trovato la soluzione finale, in quanto anche il punto E deve rimanere fermo. Possiamo dunque far ruotare il telaietto, facendo perno sui punti D ed F, di una quantità sufficiente ad annullare lo spostamento di $2δ$. In conclusione, lo spostamento dell'intero telaietto, risulta pari a 4 volte il $δ_C$ della porzione che avevo precedentemente analizzato.

Ore-uomo richieste per la compilazione della pagina.