Approccio ai fenomeni non lineari nel calcolo strutturale:

La realtà è non lineare quindi ci servirà un codice non lineare come il Marc o analoghi per simularla; in realtà la cosa non è strettamente vera, nel senso che i fenomeni non lineari vengono sostanzialmente linearizzati molto volentieri, perché una volta linearizzati si risolvono molto più semplicemente.

Noi siamo abituati a fenomeni per cui valgono le due caratteristiche che ne definiscono la linearità:

1)Scalabilità degli effetti;

2)Componibilità degli effetti.

Un problema è lineare se presenta queste 2 caratteristiche. Prendiamo un esempio di problema lineare: Una trave incastrata caricata da un carico di estremità P; chiamiamo il carico P la sollecitazione, ed andiamo ad analizzare cosa determina l’applicazione di quel carico su quella trave; consideriamo come effetto di nostro interesse la freccia δ nel punto di applicazione del carico P. Abbiamo che δ è un effetto dell’applicazione di questo carico.

La scalabilità degli effetti indica che una volta calcolata la freccia δ sotto il carico P, sappiamo che applicando un carico ad esempio di entità λP la freccia sarà λδ. Con λ scalare non ristretto in segno (positivo/negativo), di qualunque entità.

Ad esempio il fatto che λ non sia limitato in entità ci dice subito che probabilmente la linearità del problema ad un certo punto la perdiamo perché, se consideriamo un carico che è in sicurezza per quel tipo di struttura, e lo moltiplichiamo per 1 milione di volte, quella struttura non si deformerà elasticamente di 1 milione di volte in più, ma si spaccherà con un tipo di evoluzione che non è proporzionale; dal deformarsi elasticamente allo spezzarsi in due non c’è quindi un’evoluzione continua. Quindi immaginiamo che nei sistemi elastici strutturali la scalabilità degli effetti vale entro certi limiti, ossia i carichi devono essere tali da mantenere la struttura (in particolare i materiali della struttura) entro i limiti di stato tensionale accettabile; in generale per carichi sufficientemente piccoli e per λ sufficientemente piccoli (che sono quelli che studiamo nella scienza delle costruzioni standard, in cui tutto si è supposto lineare) questo principio vale.

La componibilità degli effetti può essere vista in questa maniera: Considero la stessa struttura caricata però da una coppia di estremità C; a fronte di questa coppia l’estremità si abbassa di una quantità δ’.

La componibilità degli effetti garantisce che una struttura in cui sono applicate contemporaneamente forza P e coppia C, ha lo spostamento che è la somma dello spostamento dovuto alla coppia C e lo spostamento dovuto alla forza P, quindi è uguale a δ + δ’.

Qui abbiamo un tipico problema: Se la forza da sola porta la struttura quasi al suo limite elastico e la coppia da sola porta la struttura quasi al suo limite elastico, se le applico tutte e due insieme la struttura non è più elastica. Quando per un qualunque motivo queste 2 ipotesi non sussistono, occorre studiare la stessa struttura considerando la sua natura non lineare, ossia il fatto che queste due proprietà non valgano più. Guardiamo un esempio di non linearità:

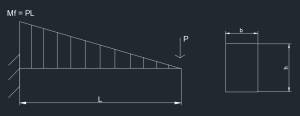
Qui abbiamo il carico P, applicato ad una trave di lunghezza L; questo carico P genera un momento flettente Mf che è massimo all’incastro e vale PL. Sappiamo che questo momento flettente genera uno stato tensionale sulla sezione terminale. Caratterizziamo la sezione terminale con il suo modulo di resistenza alla flessione W, che nel caso di sezione rettangolare di larghezza b e spessore in piano h è (b*h^2)/6 (la sezione rettangolare è un concio troncato). Il materiale ha un certo valore della tensione di snervamento Ys; sappiamo che Ys del nostro materiale moltiplicato il modulo di resistenza a flessione ((b*h^2)/6) definisce un momento flettente, che è quello oltre il quale il materiale della sezione all’incastro, comincia a plasticizzare; se il materiale comincia a plasticizzare, sappiamo che il comportamento non è più elastico ma ho una quota di plasticità; la legge di tensione-deformazione elastoplastica devia dalla linearità ed in particolare tutta la struttura devierà dalla linearità. Se questa quantità Ys*(b*h^2)/6 è maggiore del momento flettente in estremità PL il sistema non è elastico; se eccedo perdo la caratteristica di risposta elastica. Quindi la prima fonte di perdita della caratteristica elastica è il fatto che il materiale oltre certi livelli di deformazione non si comporta più elasticamente. Ovviamente possiamo calcolare lo stato della struttura ad incipiente plasticizzazione, perché ad incipiente plasticizzazione si comporta in continuità con l’ultimo stato elastico e quindi tale condizione (di incipiente plasticizzazione) della struttura può essere calcolata senza ricorrere al calcolo non lineare (perché sappiamo che l’incipiente plasticizzazione è uguale all’ultimo istante di condizione elastica che si calcola elasticamente).

Prima fonte di non linearità: il materiale si comporta linearmente solo entro un certo range di deformazione, oltre il quale il materiale non è più lineare. Questa viene chiamata non linearità legata al materiale. Il materiale si comporta non linearmente o perché ad un certo punto plasticizza (questo è tipico dei metalli) oppure perché intrinsecamente il materiale si comporta in maniera non lineare (tipico delle gomme, le gomme hanno un comportamento che non è mai lineare in nessuno dei tratti del diagramma σ-ε). Un tipico diagramma σ-ε di un materiale elastomerico è il seguente:

Si definisce un comportamento sublineare, un comportamento che devia (calando), in cui la risposta è minore della risposta linearizzata nell’intorno di un punto di riferimento. Il sistema si dice softening, quando aumenta cedevolezza con il carico; nel senso che, essendo la rigidezza di una struttura la pendenza della retta sul grafico σ-ε, se perdo pendenza all’aumentare dello stato di sollecitazione il sistema acquisisce cedevolezza e quindi diventa più morbido; viceversa se il sistema acquisisce rigidezza con la deformazione abbiamo un sistema di tipo stiffening: il sistema si irrigidisce con la sollecitazione. In realtà è interessante sapere in che caso siamo semplicemente per sapere se la nostra stima linearizzata è in eccesso o in difetto di sicurezza su una quantità. Riassumendo la non linearità può essere data dal materiale o per sua caratteristica intrinseca come gli elastomeri o perché ad un certo punto non ce la fa più e snerva.

Un'atra forma di non linearità è quella da contatto. Si suppone di analizzare la stessa trave del caso precedente caricata dallo stesso carico P, ma con la presenza di un appoggio intermedio di una certa sezione che viene toccato dalla trave dopo una certa quantità di abbas-samento libero. Questo è un fenomeno di contatto monolatero. Nel punto della trave in corrispondenza dell'appoggio può essere applicata una reazione vincolare R esercitata dall'appoggio nel caso che i due oggetti vadano in battuta. Si definisce un gioco “g” che è la distanza iniziale tra il punto più basso della trave ed i punto più alto dell'appoggio.

Le caratteristiche del contatto monolatero sono:

1) una volta definiti in maniera corretta i segni delle reazioni vincolari, R deve essere per forza tale da allontanare le superfici a contatto e quindi R≥0 secondo la convenzione di segno imposta, per cui il contatto non può attrarre i due oggetti

2) il gioco deve essere g≥0 ossia i corpi non possono compenetrarsi L'esistenza di queste due diseguaglianze viene sottolineato che il contatto è monolatero

3) il gioco e la reazione vincolare sono mutualmente esclusivi ossia g∙R =0, quindi se g≠0 allora R=0 ed i corpi non si toccano mentre se g=0 allora R≠0 e i corpi sono per forza in contatto.

Possono essere entrambi nulli solo se la trave sfiora l'appoggio ma non viene trasmessa la reazione e questa condizione è da ritenersi fisicamente ammissibile, mentre il caso di gioco e reazione entrambi diversi da zero non è ammissibile.

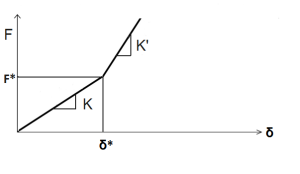
Queste tre condizioni sono storicamente chiamate Condizioni di Signorini. Come detto il contatto monolatero è non lineare e si vuole vedere il motivo della non linearità. Si considera come risposta lo spostamento δ di estremità della trave. Nell'intorno della condizione di scarico esiste un gioco macroscopico g per cui esiste un intorno della condizione di scarico per cui i corpi non si toccano e la trave si comporta come la trave senza appoggi intermedi, per cui il legame spostamento-forza è lineare ed il coefficiente di proporzionalità è il fattore K che è legato alle travi a sbalzo per cui essendo δ=Pl^2/3EJ si ha che P/δ=3EJ/l^2 che è la pendenza della curva della rigidezza della struttura pari a K. Il fattore K ha quindi un valore specifico calcolabile che sussiste finché, abbassandosi, non avviene il contatto con l'appoggio. Esisterà quindi uno spostamento δ* e un carico F* che definiscono un punto del diagramma critico oltre il quale la struttura arriva ad appoggiare. Dopo il contatto la trave si comporta con una legge carico-spostamento che è analoga al caso della stessa trave con appoggio intermedio in corrispondenza dei punti di contatto, in questo caso si aggiunge un vincolo e la struttura in particolare si comporterà in maniera più rigida.

Quindi se questa evoluzione continuasse in ipotesi lineare dopo aver rag-giunto il punto critico in cui il vincolo entra in azione la rigidezza cresce ed avrà un valore K' che è dato dal legame abbassamento-carico del caso. Il contatto monolatero causa una non linearità nella risposta del sistema perché si vede che l'evoluzione è continua ma non a derivata continua che presenta una discontinuità dopo il contatto tra trave ed appoggio. Il contatto può dar luogo anche ad un fenomeno di softening se la struttura è definita come segue:

Si ha quindi una trave su due appoggi che vengono considerati monolateri nonostante il caso di trave su due appoggi di cui uno carrello consideri quest'ultimo come vincolo bilatero, quindi per evitare di incorrere in problemi di definizione si rappresenta la trave su due appoggi monolateri. Si suppone che la trave debba sostenere un carico P in estremità, ma per evitare che la trave si distacchi dall'appoggio di sinistra bisogna applicare una forza F di precarico tra i due appoggi assimilabile ad un bullone che fa si che i due appoggi reagiscano con due reazioni vincolari pari a F/2. La trave in assenza di carico P risulta quindi precaricata e reagisce come se fosse appoggiata su due carrelli. Applicando il carico P in estremità se si va a vedere come si comporta il sistema per il solo carico P si trova che l'equilibrio si ottiene con una reazione P sull'appoggio sinistro ed una reazione 2P sull'appoggio destro. L'applicazione di P aumenta la reazione vincolare di contatto sul primo appoggio infatti il primo appoggio reagisce con più forza di repulsione, viceversa il secondo appoggio tende a scaricarsi ossia P si compone con F/2. Il sistema è lineare finché la condizione di contatto dei due appoggi è mantenuta, mentre appena cambia la con-dizione di contatto di uno dei due appoggi non si ha più la linearità. quando si trova che la reazione totale del vincolo pari a F/2-P>0 l'appoggio non è più in grado di reagire.

Si ha un grafico di questo tipo:

L'evoluzione lineare tipica della trave a sbalzo su due appoggi si ha fino a che P non raggiunge il valore F/2, dopo di che l'appoggio di sinistra perde il contatto con la trave. La struttura non potrà sostenere carichi superiori a F/2 poiché, una volta perso l'appoggio, non è più in grado di trovare un suo equilibrio. Una volta avvenuto il distacco, per il meccanismo su un solo appoggio così ottenuto qualunque spostamento δ è ammissibile. L'assunzione che abbiamo fatto è che il bullone eserciti forza costante; nella realtà quella forza aumenterà con l'allungamento, quindi il grafico devierà un po'. Ad ogni modo, osservando l'evoluzione lineare iniziale e la successiva evoluzione non lineare, siamo di fronte a un fenomeno di tipo softening. In questo caso il fenomeno softening è legato alla perdita del contatto in un qualche punto del sistema.

In definitiva, il contatto può dar luogo a fenomeni di tipo stiffening qualora si creino nuovi punti di contatto, di tipo softening qualora si perdano dei punti di contatto.

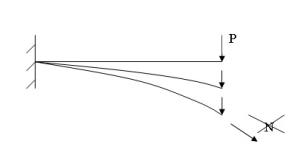
- Altro caso di non linearità è quella di natura geometrica. Una trave a sbalzo, per piccoli carichi si comporta in maniera flessionale, e la sua rigidezza è legata alla flessione della struttura, come visto in prece-denza. Quando il carico aumenta, la deflessione linearizzata prevede che ogni nodo si sposti sulla verticale; ma per deflessioni rilevanti si capisce bene che lo spostamento lungo la verticale di ogni singolo punto genera una deformata più lunga della trave di partenza. Tale allungamento può avvenire solo con l'intervento della caratteristica di sforzo normale, che ponga in trazione le fibre. Ma non essendoci questo sforzo normale, questo allungamento non può avvenire.

Nella realtà la soluzione flessionale è valida solo per piccoli spostamenti. Per spostamenti grandi, non si muove più solo sulla verticale, ma prende componente di spostamento anche orizzontale. Così il sistema evolve fino alla configurazione mostrata nella figura sotto, allorché la forza P diventa effettivamente uno sforzo normale.

Nella configurazione iniziale il comportamento della struttura è legato alla rigidezza flessionale, mentre nella configurazione finale è la rigidezza di sforzo normale che diventa preponderante nel legame tra carichi e spostamenti in quanto, come mostrato nella figura, il momento flettente nel-la configurazione deformata risulta molto più piccolo, per la diminuzione del braccio. La struttura evolve da un comportamento di tipo flessionale a un comportamento di tipo trattivo, e le travi snelle sono molto più rigide a sforzo normale che non a flessione. Per questa ragione il diagramma carico-spostamento è di tipo stiffening, come mostrato nella figura sotto.

Per piccoli carichi segue una legge dettata dalla rigidezza flessionale Kf, dopo di che evolve gradualmente fino a rigidezza KN associata a sforzo normale. È un'evoluzione continua, non esiste transizione netta da uno all'altro comportamento. Nel caso visto il materiale rimane elastico e non ci sono contatti; il fenomeno riscontrato è la non linearità dovuta a grandi spostamenti. In questo caso le caratteristiche di sollecitazione sforzo normale e mo-mento flettente calcolate sull'indeformata non sono rappresentative di quello che succede sulla deformata.

- Per motivi analoghi si può anche avere invece un fenomeno di tipo softening: consideriamo una struttura costituita da due barre rigide collegate da una cerniera; un'altra cerniera è a telaio e una terza va su un carrello agganciato a una molla. Si applica la forza F come in figura e si valuta lo spostamento δ. Con la barra inclinata di 45°, lo spostamento verticale coincide con quello orizzontale, cosicché ad abbassamento δ corrisponde schiacciamento della molla pari a 2δ.

La compressione della molla darà una certa inclinazione nel grafico F- δ, valida per un tratto lineare iniziale. Poi si arriverà alla condizione raffigurata in cui le due barre sono orizzontali, per abbassamento δ=b: questo sistema è labile, la rigidezza diventa nulla. Per piccoli spostamenti attorno a quella configurazione non ho al-cuna reazione vincolare, non si ha reazione elastica. Il grafico parte da 0 linearmente con una certa pendenza, poi tornerà a 0 con uno degli andamenti rappresentati (che andrebbe studiato con la trigonometria del problema) perché la configurazione finale per δ=b è in equilibrio per carico nullo: osservo andamento “sottolineare”, con comportamento di tipo softening, dovuto ancora una volta ai grandi sposta-menti.

Questo comportamento è tipico delle strutture instabili.

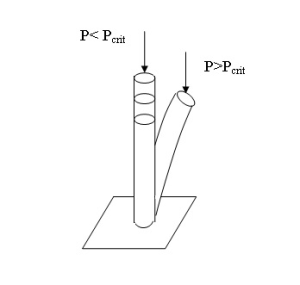
- Consideriamo una trave incastrata a un'estremità con carico di punta, che genera sforzo normale compressivo. Esiste un carico P critico per il quale si innesca l'instabilità euleriana; una volta superato Pcrit la trave evolve secondo una legge flessionale, mentre sotto Pcrit la barra subisce compressione.

Se il sistema fosse lineare, applicando un piccolo carico e valutando lo stato compressivo, per la scalabilità degli effetti, potrei riscontrare stati compressivi arbitrariamente elevati per carichi crescenti, cosicché in con-dizioni ideali questa barra dovrebbe contrarsi fino a raggiungere lunghezza nulla e in seguito anche lunghezza negativa. Con l'intervento dell'instabilità euleriana, in questo fenomeno si riscontra una non linearità di tipo geometrico, e la barra passa da una forma compressiva a una forma flessionale. Questo comportamento non si può riscontrare in ipotesi di linearità in quanto scalando la forma compressiva iniziale non si troverà mai la forma flessionale per cui la struttura arriva a rottura. Abbiamo visto la transizione tocca/non tocca che genera non linearità. Anche la presenza dell'attrito coulombiano, che dà luogo a transizione scorre/non scorre, dà fenomeni non lineari.

Considero un rotore (come in figura) avente due appoggi che ruota con una velocità angolare Ω, una massa m in un punto non esattamente sull’asse con eccentricità δ data ad esempio da tolleranze di lavorazione.

Agisce una forza centrifuga F = m Ω² δ e a causa dell’azione di tale forza il corpo si deforma (vedi figura), all’eccentricità si somma uno spostamento elastico. La forza centrifuga varia in quanto è funzione della deformata

Attraverso il seguente grafico metto in relazione la forza applicata F(u) e la reazione elastica del sistema R(u) :

nr-1d.pdf

Per u=0 si ha F = m Ω² δ. Quando R(u)= F(u) il rotore smette di deformarsi e si ha equilibrio in u* . In altri termini si ha equilibrio nel momento in cui la forza è uguale e contraria alla reazione elastica del sistema. Il problema è trovare u* ; considero la differenza fra le due funzioni in un punto u generico ed ottengo: R(u)-F(u)=r(u) dove r(u) è il residuo e rappresenta il “disequilibrio” della struttura. Tale problema è risolvibile con vari metodi numerici fra qui il metodo di bisezione e il metodo di Newton-Raphson che verrà trattato di seguito.

trattazione N-R e link RBE3 da dispensa https://cdm.ing.unimo.it/files/progettazione_assistita/dispensa_progettazione_assistita_v2.pdf

wiki N-R prog. ass. (work in progress) Algoritmo Newton-Raphson per sistemi di equazioni non lineari : Iterazione base

wiki RBE3 prog. ass. (work in progress) Link di forze/momenti risultanti distributi RBE3

slide ing. Mantovani: link_di_forze_rev05x.pdf lezione_piastre_rev01x.pdf