Indice
Elemento isoparametrico 4 nodi
Quadrilatero 4 nodi
Nell' analisi FEM il quadrilatero 4 nodi, insieme al triangolare 3 nodi, è l’elemento basilare su cui costruire un modello e appare più vantaggioso dell’altro rapportandone l’accuratezza dei risultati con la finezza della mesh.
Come già visto negli elementi triangolari il campo degli spostamenti di ciascun lato è definito per interpolazione degli spostamenti nodali.
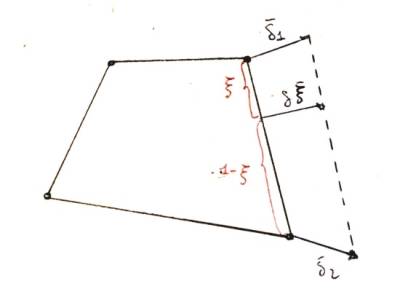
Per i quadrilateri 4 nodi l’interpolazione è lineare, come si vede in Fig.1:
$\overline{\delta }_{\xi }= \left ( 1-\xi \right )\overline{\delta }_{1}+\xi \overline{\delta _{2}}$
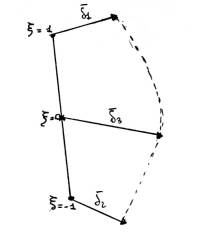
Altrimenti, introducendo nodi ai centri lato, l’interpolazione è al più parabolica e l’elemento in questione prende il nome di quadrilatero 8 nodi:
$\bar{{\delta }_{\xi }}={N}_{1}\left(\xi \right)\bar{{\delta }_{1}}+{N}_{2}\left(\xi \right)\bar{{\delta }_{2}}+{N}_{3}\left(\xi \right)\bar{{\delta }_{3}}$
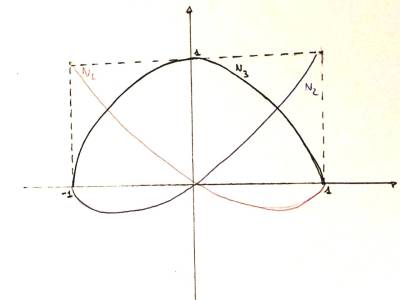
Considero funzioni di forma quadratiche; ${N}_{1}\left(\xi \right)$ è una parabola che assume valore 1 in -1 e 0 negli altri 2 punti:
${N}_{1}\left(\xi \right)=\left(\xi - 0 \right)\left(\xi - 1 \right)\alpha $ , con α tale che ${N}_{1}\left(\ -1 \right)=1$
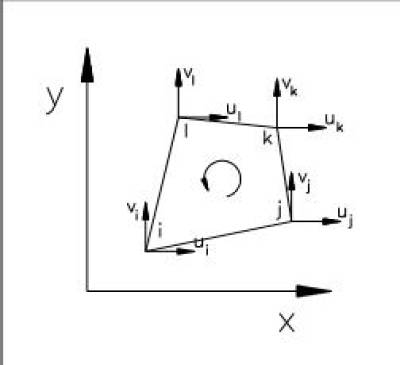
Si consideri ora nel piano XY un quadrilatero a 4 nodi arbitrariamente distorto:
L’elemento possiede 2 gradi di libertà per ogni nodo, pertanto le funzioni di interpolazione saranno definite in funzione di 8 coefficienti incogniti:
$u=a+bx+cy+dxy$
$v=e+fx+gy+hxy$
Rispetto al triangolare 3 nodi i due coefficienti aggiuntivi descrivono un contributo quadratico “dxy”; denominato “bilineare”.
Il nome è dovuto al fatto che la sua variazione lungo la direzione di un asse di riferimento, tenuto costante l’altro, darà sempre contributo lineare.
Mentre invece risulterà quadratico seguendo ogni altra direzione.
Continuità degli spostamenti
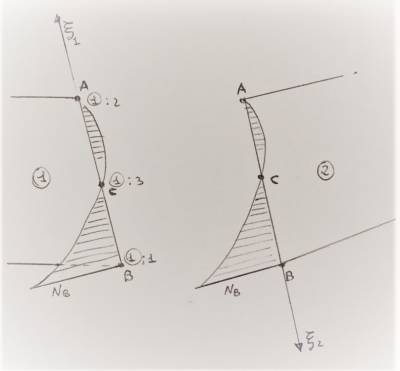
In elementi quadrilateri 4 nodi arbitrariamente distorti tuttavia il contributo bilineare comporta l’insorgere di problemi legati alla continuità degli spostamenti.
Si consideri l’esempio in figura con 2 quadrilateri adiacenti.
Tutti i nodi dell’elemento 1 sono incernierati, dunque il campo degli spostamenti è identicamente nullo e il corrispondente sistema è omogeneo.
$u\left({x}_{1},{y}_{1} \right)= {U}_{1}=0$
$v\left({x}_{1},{y}_{1} \right)= {V}_{1}=0$
$u\left({x}_{2},{y}_{2} \right)= {U}_{2}=0$
$v\left({x}_{2},{y}_{2} \right)= {V}_{2}=0$
$u\left({x}_{3},{y}_{3} \right)= {U}_{3}=0$
$v\left({x}_{3},{y}_{3} \right)= {V}_{3}=0$
$u\left({x}_{4},{y}_{4} \right)= {U}_{4}=0$
$v\left({x}_{4},{y}_{4} \right)= {V}_{4}=0$
L’elemento 2 presenta invece uno spostamento δ in direzione perpendicolare all’asse del carrello, che può comportare uno spostamento non nullo sul lato di adiacenza causato dal termine bilineare.
Ciò non sarebbe accaduto se gli elementi quadrilateri avessero lati opposti paralleli e ben orientati rispetto agli assi del sistema di riferimento.
Essendo ad esempio il lato verticale in figura parallelo ad y il termine bilineare non da contributo quadratico, il campo degli spostamenti è dunque ben definito dall’interpolazione lineare degli spostamenti ai nodi 1-4.
Un’altra modalità per garantire la continuità degli spostamenti è l’introduzione dei nodi a centro lato, passando ad un elemento quadrilatero 8 nodi e quindi a campi di spostamenti di ordine quadratico.
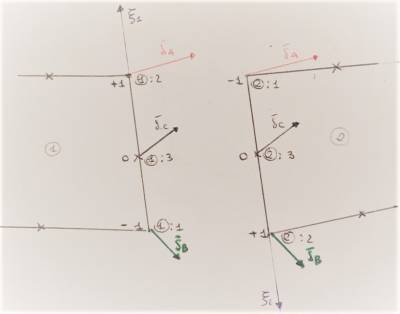
$\displaystyle \overline\delta_{\ \xi1 } = N_{\ 1:2}\overline\delta_{\ 1:2 } + N_{\ 1:1}\overline\delta_{\ 1:1 } + N_{\ 1:3}\overline\delta_{\ 1:3 }$
$\displaystyle \overline\delta_{\ \xi2 } = N_{\ 2:2}\overline\delta_{\ 2:2 } + N_{\ 2:1}\overline\delta_{\ 2:1 } + N_{\ 2:3}\overline\delta_{\ 2:3 }$
Avendo posto δ come vettore degli spostamenti nodali e gli assi coordinati $\displaystyle \xi_{\ 1 } = - \xi_{\ 2 }$.
Si ha continuità in questo caso se gli spostamenti ai nodi del lato di contatto sono uguali per entrambi gli elementi e se vengono modulati con le stesse funzioni di forma.
$\displaystyle \overline\delta_{\ a} = \overline\delta_{\ 1:2} = \overline\delta_{\ 2:1}$
$\displaystyle \overline\delta_{\ b} = \overline\delta_{\ 1:1} = \overline\delta_{\ 2:2}$
$\displaystyle \overline\delta_{\ c} = \overline\delta_{\ 1:3} = \overline\delta_{\ 2:3}$
$\displaystyle N_{\ a} = N_{\ 1:2} = N_{\ 2:1}$
$\displaystyle N_{\ b} = N_{\ 1:1} = N_{\ 2:2}$
$\displaystyle N_{\ c} = N_{\ 1:3} = N_{\ 2:3}$
Coordinate fisiche e naturali
Lo svantaggio nell'utilizzo dell’elemento quadrilatero 8 nodi risiede nella complessità di calcolo maggiore rispetto al 4 nodi, tuttavia non è sempre possibile garantire una perfetta regolarità di quest’ultimo.
Per risolvere il problema si definisce un nuovo sistema di coordinate, dette naturali.
Nel sistema di coordinate naturali l’elemento è sempre un quadrato che si estende su ξ e η da -1 a +1, e ogni punto del sistema fisico può essere espresso come funzione di questi due parametri.
Dal punto di vista grafico è possibile individuare una corrispondenza tra i due sistemi, considerando ogni punto sul piano naturale come intersezione di due rette parallele agli assi ξ e η.
In questo modo si intercettano delle coordinate muovendosi nelle direzioni degli assi di riferimento, dove la mappatura avrà caratteristica lineare.
Questa proprietà garantisce ad esempio che il punto medio di un segmento ben orientato rispetto agli assi naturali risulti punto medio del reciproco segmento fisico distorto.
Ad esempio il centroide dell’elemento (fig.10), di coordinate naturali ξ=0 η=0, risulterà essere il punto medio della mediana passante per i lati opposti 34–12, motivo per cui generalmente non corrisponderà col baricentro di un elemento arbitrariamente distorto.
Si procede con la definizione delle funzioni di mappatura come combinazione lineare dei nodi sul piano fisico, pesate mediante le funzioni di forma $\displaystyle N_{\ 1, 2, 3, 4}$.
$\displaystyle N_{\ 1 } = a\xi + b\eta +c\xi\eta +d$
L'elemento risulta non distorcersi mai sul piano naturale e imponendo dei valori sui 4 nodi ottengo i coefficienti a,b,c,d. Sapendo che le funzioni di forma valgono 1 sul nodo stesso e 0 sui restanti ottengo per il nodo 1 il seguente sistema:
$\displaystyle N_{\ 1 }(-1;-1) = 1$
$\displaystyle N_{\ 1 }(-1;1) = 0$
$\displaystyle N_{\ 1 }(1;-1) = 0$
$\displaystyle N_{\ 1 }(1;1) = 0$
Risolvendo:
$\displaystyle N_{\ 1 } = \frac{(1-\xi)(1-\eta) }{4}$
Si può così risalire ad una generica espressione per le funzioni di forma:
$\displaystyle N_{\ 1, 2, 3, 4 } = \frac{(1\pm\xi)(1\pm\eta) }{4}$
Correggendo il segno in base alla caratteristica della funzione di essere unitaria sul nodo stesso e nulla sugli altri.
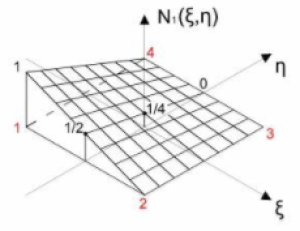
In generale la funzione di forma è bilineare, ma fissando uno tra ξ e η si può considerare lineare sui 4 lati nel sistema di coordinate naturali. Rappresentiamo perciò l'andamento della funzione di forma $\displaystyle N_{\ 1}$:
Possiamo trovare il valore della funzione di forma in un punto generico:
- Prendo e traccio la parallela a uno dei due assi passante per quel punto;
- Definisco perciò due punti sui lati;
- Associati a quei due punti ho due valori della funzione di forma;
- Interpolo linearmente i due valori di N trovati;
- Ottengo il valore della funzione di forma associata al generico punto.
Una volta ricavate le $\displaystyle N_{\ 1, 2, 3, 4}$ si può definire la mappatura delle coordinate come combinazione lineare avente come pesi le funzioni di forma stesse:
$\displaystyle x(\xi;\eta)= N_{\ 1}x_{\ 1} + N_{\ 2}x_{\ 2} + N_{\ 3}x_{\ 3} + N_{\ 4}x_{\ 4} $
$\displaystyle y(\xi;\eta)= N_{\ 1}y_{\ 1} + N_{\ 2}y_{\ 2} + N_{\ 3}y_{\ 3} + N_{\ 4}y_{\ 4} $
Occorre precisare che non sempre l'operazione di mappatura inversa è possibile, visto che le $\displaystyle N_{\ 1, 2, 3, 4}$ sono quadratiche in ξ e η e invertendole non si otterrebbe una soluzione univoca, se non con particolari requisiti di regolarità.
$\displaystyle N_{\ 1}(\xi;\eta)x_{\ 1} + N_{\ 2}(\xi;\eta)x_{\ 2} + N_{\ 3}(\xi;\eta)x_{\ 3} + N_{\ 4}(\xi;\eta)x_{\ 4}=x_{\ noto} $
$\displaystyle N_{\ 1}(\xi;\eta)y_{\ 1} + N_{\ 2}(\xi;\eta)y_{\ 2} + N_{\ 3}(\xi;\eta)y_{\ 3} + N_{\ 4}(\xi;\eta)y_{\ 4}=y_{\ noto} $
In pratica non sempre ad un punto fisico P(x;y) si riesce ad associare un solo punto P’(ξ;η) nel piano naturale.
Sempre con le stesse modalità, anche il campo degli spostamenti di un punto fisico può esprimersi come interpolazione delle stesse funzioni di forma nel piano naturale:
$\displaystyle u(\xi;\eta)= N_{\ 1}u_{\ 1} + N_{\ 2}u_{\ 2} + N_{\ 3}u_{\ 3} + N_{\ 4}u_{\ 4} $
$\displaystyle v(\xi;\eta)= N_{\ 1}v_{\ 1} + N_{\ 2}v_{\ 2} + N_{\ 3}v_{\ 3} + N_{\ 4}v_{\ 4} $
Utilizzando le stesse leggi di interpolazione per coordinate e spostamenti l’elemento in questione viene definito isoparametrico.