L’analisi statica di un sistema può essere condotta quando siano note la matrice di rigidezza, e le forze esterne agenti su di esso o gli spostamenti imposti. L’equazione dell’ equilibrio statico consta del solo termine elastico e le grandezze del problema sono costanti nel tempo per ipotesi assunta.
In presenza di sollecitazioni o spostamenti variabili nel tempo, l’analisi dinamica contempla anche l’influenza nell’equazione del moto di fenomeni viscosi e inerziali, essendo questi proporzionali alle derivate temporali del moto stesso, prime e seconde rispettivamente.
È possibile definire anche sistemi speciali, per i quali l’evoluzione delle grandezze d’interesse avviene con una pulsazione estranea al range frequenziale sensibile del sistema. Per pulsazioni molto inferiori alla prima pulsazione naturale si tratta di sistemi quasi-statici, nella cui dinamica è possibile trascurare la dipendenza dalle azioni viscose e inerziali; invece per pulsazioni molto elevate avrà effetto utile solo il valore medio dell’oscillazione.
Con riferimento all’elemento finito, si è già definita la matrice di rigidezza nella caratterizzazione dello stato di equilibrio elastico. Nella generalizzazione del problema ad affrontare l’analisi dinamica del moto, occorre una definizione univoca della matrice di massa dell’elemento, per descrivere l’equazione del moto completa
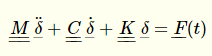 Quanto alla matrice di smorzamento, la sua definizione risulta più problematica (in particolare
in quei casi di smorzamento strutturale di difficile quantificazione. Viceversa l’utilizzo di smorzatori viscosi con parametri noti a priori, permette di modellare una matrice di smorzamento coerente e ben definita). Tale argomento verrà affrontato in un capitolo successivo.
Quanto alla matrice di smorzamento, la sua definizione risulta più problematica (in particolare
in quei casi di smorzamento strutturale di difficile quantificazione. Viceversa l’utilizzo di smorzatori viscosi con parametri noti a priori, permette di modellare una matrice di smorzamento coerente e ben definita). Tale argomento verrà affrontato in un capitolo successivo.
Matrice di massa per l’elemento finito
Si considera un volume di materiale $\Omega$, un sistema di coordinate globali $(x, y, z)$ ed un sistema di coordinate locali $(\xi, \eta, \zeta)$.
Siano le funzioni di forma vettore
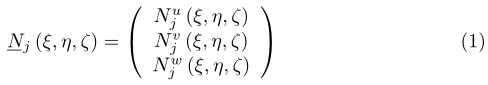 che leghino il j-esimo grado di libertà alle componenti globali di spostamento di un punto interno al dominio, individuato in coordinate locali.
La natura degli
che leghino il j-esimo grado di libertà alle componenti globali di spostamento di un punto interno al dominio, individuato in coordinate locali.
La natura degli  è propria dello specifico elemento; ad esempio per un elemento isoparametrico piano a 4 nodi, con nodi numerati (1,2,3,4), si devono ottenere i risultati a cui si è già pervenuti per questo elemento, allora si deduce
è propria dello specifico elemento; ad esempio per un elemento isoparametrico piano a 4 nodi, con nodi numerati (1,2,3,4), si devono ottenere i risultati a cui si è già pervenuti per questo elemento, allora si deduce
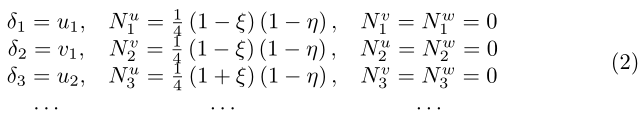 Il campo degli spostamenti
Il campo degli spostamenti 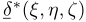 è quindi una funzione vettoriale che restituisce le componenti globali di spostamento $(x, y, z)$ di un punto interno del dominio, nota la sua posizione in coordinate locali $(\xi, \eta, \zeta)$ nel piano naturale
è quindi una funzione vettoriale che restituisce le componenti globali di spostamento $(x, y, z)$ di un punto interno del dominio, nota la sua posizione in coordinate locali $(\xi, \eta, \zeta)$ nel piano naturale
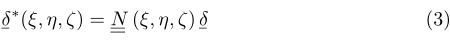 ove
ove
 è la matrice delle funzioni di forma $3 \times n$, con $n$ numero di gradi di libertà nodali totali dell’elemento, e
è la matrice delle funzioni di forma $3 \times n$, con $n$ numero di gradi di libertà nodali totali dell’elemento, e
 è il vettore contenente tali gradi di libertà.
Non essendo tali funzioni di forma dipendenti dal tempo, si ha che il campo delle velocità è rappresentabile semplicemente come
è il vettore contenente tali gradi di libertà.
Non essendo tali funzioni di forma dipendenti dal tempo, si ha che il campo delle velocità è rappresentabile semplicemente come
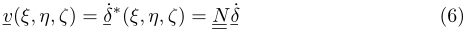 Ove
Ove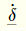 è il vettore delle velocità nodali, contente le derivate nel tempo discrete dei valori di spostamento ai vari gradi di libertà.
è il vettore delle velocità nodali, contente le derivate nel tempo discrete dei valori di spostamento ai vari gradi di libertà.
Considerata l’energia cinetica propria del materiale compreso entro l’elemento nella forma
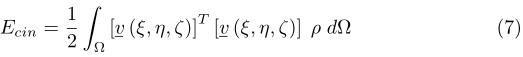 Ove $\rho$ è la densità puntuale del materiale, è possibile ivi sostituire la forma generica della velocità puntuale con la definizione della stessa in (6), ottenendo
Ove $\rho$ è la densità puntuale del materiale, è possibile ivi sostituire la forma generica della velocità puntuale con la definizione della stessa in (6), ottenendo
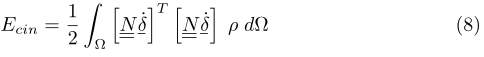 Ricordando infine che
Ricordando infine che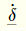 non varia nelle variabili di integrazione, otteniamo la forma
non varia nelle variabili di integrazione, otteniamo la forma
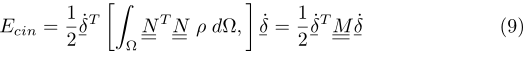 da si giunge alla definizione di una matrice
da si giunge alla definizione di una matrice 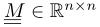 detta matrice di massa congruente per l’elemento. L’integrazione entro (9) può essere condotta per quadratura gaussiana, in analogia con la definizione di matrice di rigidezza; in particolare si può scrivere
detta matrice di massa congruente per l’elemento. L’integrazione entro (9) può essere condotta per quadratura gaussiana, in analogia con la definizione di matrice di rigidezza; in particolare si può scrivere
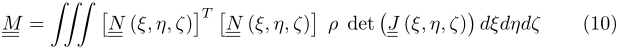 ove
ove  è lo Jacobiano della mappatura $(\xi, \eta, \zeta) → (x, y, z)$.Possiamo scrivere la variazione di energia cinetica dell’elemento
è lo Jacobiano della mappatura $(\xi, \eta, \zeta) → (x, y, z)$.Possiamo scrivere la variazione di energia cinetica dell’elemento
 ove in (12), data la natura scalare del primo termine è possibile riscriverlo come trasposto.
ove in (12), data la natura scalare del primo termine è possibile riscriverlo come trasposto.
Eguagliando la variazione di energia cinetica alla potenza fornita da un sistema di forze esterne 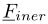 agenti sui nodi dell’elemento (tali forze equilibrano sul nodo le reazioni inerziali, e quindi sono ad esse uguali e contrarie)
agenti sui nodi dell’elemento (tali forze equilibrano sul nodo le reazioni inerziali, e quindi sono ad esse uguali e contrarie)
 otteniamo la relazione
otteniamo la relazione
 che lega le forze da applicare all’elemento affinchè questo acceleri con determinate accelerazioni nodali (derivate seconde nel tempo degli spostamenti ai vari gg.d.l).
che lega le forze da applicare all’elemento affinchè questo acceleri con determinate accelerazioni nodali (derivate seconde nel tempo degli spostamenti ai vari gg.d.l).
