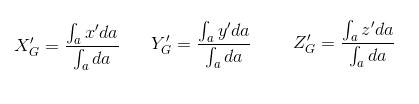Indice
Stato tensionale e stato deformativo nelle travi
Per deformazione s’intende il processo di cambiamento di forma del corpo (supposto continuo e deformabile). Supponendo di applicare ad un mezzo continuo, già in equilibrio sotto l’azione di certe azioni, un sistema di azioni aggiuntive, si provocano generalmente in esso delle variazioni di configurazione (spostamenti). Possono esistere spostamenti per i quali non variano le posizioni relative delle singole parti del mezzo continuo, e quindi le distanze relative tra i suoi punti: si tratta di moti rigidi o, più precisamente, di traslazioni e rotazioni rigide. Epurando il campo di spostamenti dai moti rigidi si ottiene la deformazione pura subita dal mezzo continuo. Per una valutazione della deformazione che il mezzo continuo subisce si assume che il campo di spostamento del solido strutturale sia congruente:
- Esternamente: in corrispondenza dei punti vincolati sulla frontiera del volume, il campo di spostamento è compatibile con i vincoli stessi.
- Internamente: nel volume del continuo materiale non si verificano né distacchi (fratture), né compenetrazioni di materia.
Ovviamente da un punto di vista ingegneristico è ragionevole lavorare in ipotesi di piccoli spostamenti. Lo stato deformativo che subisce un corpo viene quantificato attraverso analisi tensoriali e si rimanda ai testi di Scienza delle Costruzioni per una descrizione piu accurata. In poche parole nel processo di deformazione possiamo avere:
- Un campo di deformazione lineare: valuta in ogni punto del corpo l’entità delle variazioni di dimensioni infinitesime ε lungo assegnate direzioni (parallele agli assi del sistema di riferimento).
- Un campo di deformazione angolare: valuta in ogni punto del corpo l’entità delle variazioni di forma infinitesime $\gamma$ fra assegnate direzioni ortogonali. Tali variazioni di forma vengono quantificate mediante variazioni di angoli tra direzioni ortogonali.
In situazioni generali, che costituiscono la maggior parte dei casi, il campo (tensoriale) di deformazione varia da punto a punto e avrà una espressione del genere:
$$ \varepsilon = \begin{bmatrix} \varepsilon _{x} & \gamma _{xy} & \gamma _{xz} \\ \gamma _{yx} & \varepsilon _{y} & \gamma _{yz}\\ \gamma _{zx} & \gamma _{zy} & \varepsilon _{z} \end{bmatrix} $$
Evitando la notazione tensoriale (non svolta in classe, se ben ricordo, ndEB) si possono scrivere semplicemente le 6 componenti di deformazione indipendenti
$$ \underline{\epsilon} = \begin{bmatrix} \epsilon_{x}&\epsilon_{y}&\epsilon_{z}& \gamma_{xy}& \gamma_{yz}& \gamma_{zx} \end{bmatrix}^T $$
Tale tensore si dimostra essere simmetrico; i termini sulla diagonale rappresentano le dilatazioni del corpo, mentre tutti gli altri rappresentano le distorsioni angolari. Di seguito è riportata una rappresentazione qualitativa di quanto appena detto.
Figura 1: Elemento infinitesimo soggetto a dilatazione lineare
Analogamente:
Figura 2: Elemento infinitesimo soggetto a deformazione angolare
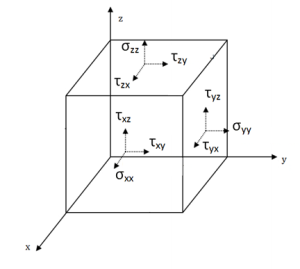
Definendo un cubetto di dimensioni infinitesime è possibile valutare i vari tipi di tensione che si riscontrano. In particolare si contraddistinguono con la lettera σ tutti gli sforzi che sono normali ad una superficie, mentre con la lettera τ tutti gli sforzi che giacciono sulla superficie. Per quanto riguarda invece i pedici, noto che ogni sforzo è contraddistinto con due lettere. Per esempio $\tau_{xy}$:
- la prima lettera (x) indica la direzione normale alla superficie sulla quale è applicata tale tensione;
- la seconda lettera (y) indica la direzione di tale tensione;
Dunque con τxy stiamo valutando la tensione tangenziale applicata alla superficie normale all’asse x in direzione y
Figura 3: Stato tensionale su cubetto infinitesimo
Brevemente possiamo definire il tensore delle tensioni come:
$$ \sigma = \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{bmatrix} $$
Evitando sempre la notazione tensoriale (non svolta in classe, se ben ricordo, ndEB) si possono scrivere semplicemente le 6 componenti di tensione indipendenti
$$ \underline{\sigma} = \begin{bmatrix} \sigma_{x}&\sigma_{y}&\sigma_{z}& \tau_{xy}& \tau_{yz}& \tau_{zx} \end{bmatrix}^T $$ Queste componenti di tensioni sono legate alle deformazioni attaverso il modulo di elasticità longitudinale e tangenziale come riportato nelle seguenti formule:
NOOOOO!! $$ \sigma _{ij}=E\varepsilon _{ij} $$ NOOOOO!! Solo se $\nu=0$, $i=j$ !!!!
oppure, forse,
$$ \sigma _{ij}=E_{ijkl}\varepsilon _{kl} $$
ma lasciam perdere la notazione tensoriale (ndEB).
Valgono invece per un materiale elastico lineare omogeneo isotropo le relazioni
$$ \begin{bmatrix} \sigma_{x} \\ \sigma_{y} \\ \sigma_{z} \end{bmatrix} = \frac{E}{\left(1+\nu\right)\left(1-2\nu\right)} \begin{bmatrix} 1-\nu &\nu &\nu \\ \nu & 1-\nu & \nu \\ \nu & \nu & 1-\nu \end{bmatrix} \begin{bmatrix} \epsilon_{x} \\ \epsilon_{y} \\ \epsilon_{z} \end{bmatrix} $$
e
$$ \begin{bmatrix} \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} = G \begin{bmatrix} \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} $$
vedi https://en.wikipedia.org/wiki/Hooke%27s_law#Isotropic_materials
$$ \tau _{ij}=G\gamma _{ij} $$
$$ G=\frac{E}{2(1+\nu )} $$
Dove con $$\sigma_{ii}$$ si indicano le tensioni assiali o normali, mentre con $$\tau_{ij}$$si indicano le tensioni tangenziali. Queste tensioni appena citate possono nascere in seguito ad una serie di sollecitazioni a cui può essere sottoposto un generico corpo o trave.
Il materiale è supposto isotropo e lineare, anche se non necessariamente omogeneo.
La trattazione di sforzo normale e momento flettente può essere estesa a materiali ortotropi con asse di ortotropia allineato con asse della trave.
Sforzo Normale
Si considera una sezione di una trave con un sistema locale di riferimento baricentrico, dunque con origine nel punto G. Il baricentro, o centro di massa, ha coordinate rispetto ad un sistema di riferimento fisso date da queste formule:
Coordinate baricentro
Dove a rappresenta l’area della sezione , x’ y’ e z’ rappresentano le coordinate rispetto ad un sistema di riferimento fisso.
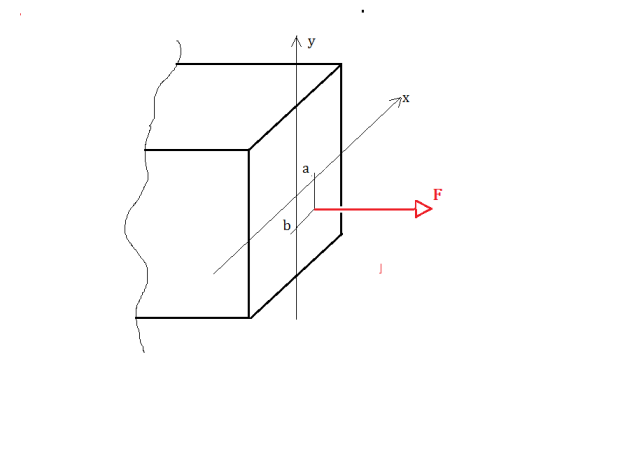
Immagino ora di considerare una semplice trave a sezione rettangolare e applicare in un punto di una sua sezione un certo carico F.
Carico eccentrico
Si spostano ora il carico F sul baricentro e si evidenziano i momenti di trasporto generati, saranno due momenti flettenti mx e my.
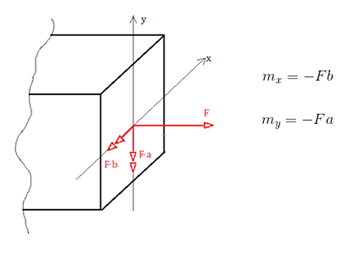
In tal caso allora risulta evidente che il solido viene sollecitato a sforzo normale e a flessione lungo gli assi x e y.
Momento flettente
Una trave si dice essere soggetta a momento flettente nel momento in cui lungo gli assi ortogonali a quello della trave agiscono delle coppie (tali assi sono x e y per il sistema di riferimento considerato). Il momento è detto flettente poiché in grado di imprimere una curvatura locale, nel suo punto di applicazione. Ipotesi di base a Flessione: le sezioni piane soggette a sollecitazioni di flessione rimangono piane; la fibra baricentrica non si flette/deforma durante la sollecitazione.
Consideriamo la sezione di un materiale non uniforme, avente un modulo di Young (E) non costante;

Figura 1: Sezione non uniforme
Gli assi x, y, z sono assi locali con z localmente tangente all’asse baricentrico. Se l’asse x o l’asse y sono di simmetria, essi saranno assi principali d’inerzia.
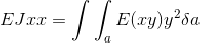
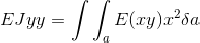
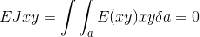 se x e y sono assi principali d’inerzia.
se x e y sono assi principali d’inerzia.
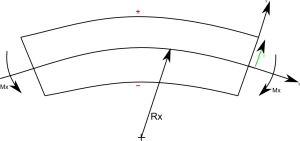
Figura 2: Curvatura lungo l'asse x
Curvatura: 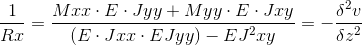

Figura 3: Curvatura lungo l'asse y
Curvatura: 
v : spostamento del baricentro in direzione y ;
u : spostamento baricentro in direzione x ;
Deformazione assiale: 
Altre deformazioni:
$ \varepsilon _{x}= \varepsilon _{y} = - \nu \varepsilon _{z} $

Nella flessione si ha anche l’effetto Poisson: 
Figura 4: Effetto Poisson
Stato tensionale:
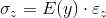 [ tensioni lineari su sezione solo se E è omogeneo]
[ tensioni lineari su sezione solo se E è omogeneo]
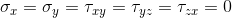
Su MATERIALE OMOGENEO:
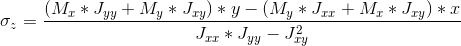
Figura 5: Diagramma tensioni a farfalla momento flettente.
Con asse neutro baricentrico pongo τz = 0;
I punti più critici sono quelli più lontani dall’asse neutro, nei quali la tensione flessionale sarà massima.
Ovviamente quanto trattiamo un materiale non omogeneo abbiamo uno stato tensionale che è diverso a seconda del materiale. Questo è legato al fatto che sono caratterizzati da un diverso modulo di Young. Ovviamente i due materiali sono soggetti a identica deformazione (i due materiali in tal caso si possono considerare come due molle in serie che sono soggette alla stessa freccia ma che si ripartiscono il carico: la molla che presenta una rigidezza più elevata sarà soggetta ad una forza maggiore)
Taglio, 1a parte
Lo sforzo di taglio è una tipologia di sollecitazione a cui può essere soggetto un corpo; tale stato induce anche una variazione di momento flettente.
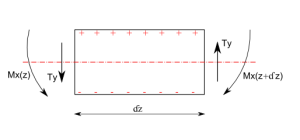
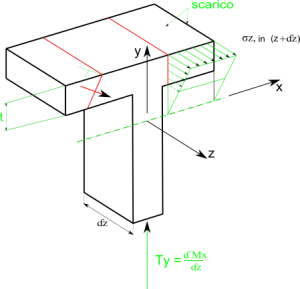
Consideriamo un concio di trave bidimensionale (con asse z asse della trave) sollecitato con una coppia di forze Ty uguali e opposte a una distanza infinitesima dz (fig 1). Sul concio agiranno per l’equilibrio alla rotazione due coppie Mx(z) e Mx(z+dz).
Fig.1
Nello specifico si ha:
• per un momento lungo x (1) :
$$ T_{y}=\frac{dM_{x}}{dz} $$
• per un momento lungo y (2):
$$ T_{x}=-\frac{dM_{y}}{dz} $$ La sollecitazione tagliante dipenderà quindi da :
• coordinate x,y ;
• momento flettente lungo x Mx ;
• momento flettente lungo y My ;
• momento di inerzia Jxx ;
$$ \sigma_{z}=f\left ( x , y , M_{x}, M_{y},J_{xx},J_{yy},J_{xy} \right ) $$
Nel caso in cui si abbia una sezione costante la variazione della sollecitazione tagliante rispetto alla coordinata z sarà funzione di : $$ \frac{d\sigma_{z}}{dz}=f\left ( x , y ,\frac{dM_{x}}{dz} ,\frac{M_{y}}{dz} ,J_{xx},J_{yy},J_{xy} \right ) $$ o equivalentemente ( valgono le relazioni (1) e (2) ) :
$$ \frac{d\sigma_{z}}{dz}=f\left ( x , y ,T_{y} ,-T_{x} ,J_{xx},J_{yy},J_{xy} \right ) $$
le relazioni trovate sono valide $ \forall x,y $ della sezione, dunque J** viene sostituito con Jxx e Jyy.
Taglio secondo la teoria di Jourawsky
La trattazione di Jourawsky relativamente alla sforzo di taglio risulta essere una trattazione approssimata.
Si ricavano infatti le tensioni tangenziali nel rispetto delle sole condizioni di equilibrio tralasciando le condizioni di congruenza.
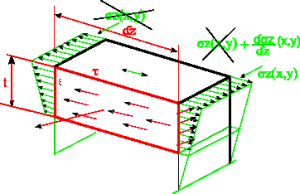
Si consideri una trave caricata con una forza Ty applicata nel baricentro G (fig 2); isolato un concio elementare di spessore t e lunghezza dz si osserva che la superficie laterale del concio risulta essere scarica (fig 3) . Le sollecitazioni taglianti $ \tau $ agiscono ortogonalmente alla normale della faccia $ \xi $ lungo la direzione z . In generale le $ \tau $ risultano essere uniformi, in caso contrario se ne considera un valore medio $ \overline{\tau} $ .
Fig. 2 Fig. 3
Dall’ equilibrio sulla sezione si ottiene la relazione tra tensioni tangenziali e sforzo tagliante:
$$ \overline{\tau }*t*dz = \iint_{a*} \frac{d\sigma_{z}(x,y)}{dz} * dz*da $$
Semplificando si ottiene la formula di Jourawsky :
$$ \overline{\tau }*t = \iint_{a*} \frac{d\sigma_{z}}{dz}*da $$
Consideriamo il caso in cui sulla sezione lo sforzo di taglio agisce sull'area a* (fig 4-5); in presenza di materiale omogeneo la sollecitazione sarà pari a :
$$ q=\overline{\tau}*t=\frac{(T_{x}*J_{xx}-T_{y}*J_{xy})*A^{*}*\bar{x^{*}}-(T_{x}*J_{xy}- T_{y}*J_{yy})*A^{*}*\bar{y^{*}}}{J_{xx}*J_{yy}-J^{2}_{xy}} $$ dove :
• $ A^{*}*\bar{x}^{*} =\iint_{a^{*}}x*da $
• $ A^{*}*\bar{y}^{*} =\iint_{a^{*}}y*da $

Fig.4
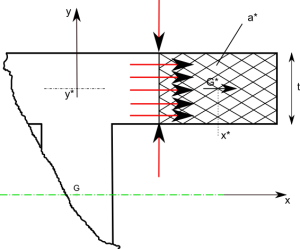
Fig.5
E’ opportuno sottolineare il fatto che con la trattazione secondo Jourawsky si considera un valore medio della sollecitazione tagliante $ \overline{\tau} $; nei casi reali non è corretto considerare tale valore come valore medio puntuale (fig 6 -confronto tra andamento effettivo ,in blu, e valor medio calcolato con Jourawsky ,in rosso).
(Per la soluzione esatta dello sforzo di taglio vedere : A. E. H. Love – “A Treatise on the Mathematical Theory of Elasticity”)
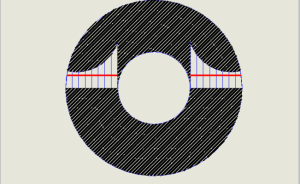
Fig.6
Angelo Pignatelli 212060
Massimo Sabato 219134
Antonello Sileo 215304
Alessio Bertoldi 214748
| Autori/Revisori | Prima stesura | Prima revisione | Seconda Stesura | Seconda revisione | Totale |
| Alessio Bertoldi | 4 | 1 | 5 | ||
| Antonello Sileo | 4 | 1 | 5 | ||
| Angelo Luigi Pignatelli | 4 | 1 | 5 | ||
| Massimo Sabato | 4 | 1 | 5 | ||
| revisore 1 | 1 | 3 | |||
| revisore 2 | 2 | ||||
|---|---|---|---|---|---|
| revisore 3 | |||||
| revisore 4 | |||||
| Totale | 16 | 3 | 4 | 0 | 23 |