Indice
giavotto-polimi-teoria_della_piastra_sottile.pdf
Teoria delle Piastre
Con il termine piastre ci riferiamo a strutture aventi spessore molto minore delle dimensioni caratteristiche quali ad esempio lunghezza o larghezza.
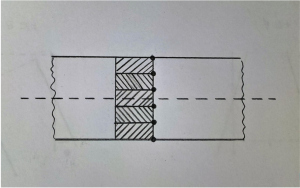
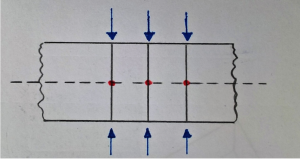
Prendendo in considerazione una generica porzione di piastra, questa può esser modellata attraverso elementi solidi. Assumendo cinque elementi abbiamo una situazione di questo tipo:
Ai cinque elementi sono associati sei nodi che corrispondono a 18 gradi di libertà. Per procedere ora ad un’analisi più precisa, potremmo pensare di introdurre una cinematica ad hoc per le piastre, per fare ciò consideriamo dei segmenti rigidi in cui gli unici gradi di libertà sono le rototraslazioni di questi. Ad ogni rototraslazione del nodo corrisponde una rototraslazione del segmento corrispondente.
Si definisca un sistema di riferimento locale e non globale, in cui l’asse z è normale alla superficie media.
Per l’individuazione della superficie media di una piastra distinguiamo due casi. Se lo spessore è uniforme consiste in una semplice intersezione dei punti medi dei segmenti. Se lo spessore non è uniforme si può procedere individuando un punto sulla superficie superiore, il corrispondente punto della superficie inferiore a minima distanza e quindi il punto medio del segmento che li congiunge. Ripetendo il procedimento per un numero sufficiente di punti e congiungendo tutti i punti medi ottengo la superficie media.
La rotazione del segmento intorno l’asse z (detta drilling) trasforma l’elemento in sé stesso, non ha perciò senso fisico in quanto non induce deformazioni nel materiale. Non tutti i gradi di libertà del segmento corrispondono a delle vere e proprie deformazioni, come nel caso dell’asse z a cui non è associata variazione di energia potenziale elastica.
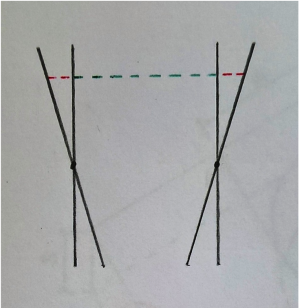
In generale, a rotazioni intorno y, possono essere associate variazioni di energia potenziale elastica dovute alle deformazioni.
[con deformazione]
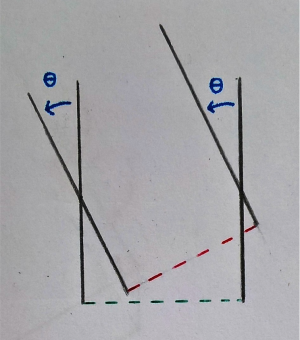
Non sempre però questo avviene, come nel controesempio seguente.
[rotazione intorno y con traslazione, senza deformazione (nessuna variazione di energia potenziale elastica)]
La rappresentazione attraverso segmenti rigidi, non consente di gestire lo schiacciamento della piastra dovuto a pressione sulle pareti.
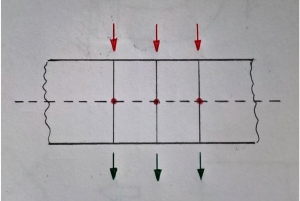
La rappresentazione dei carichi distribuiti sulla superficie consente di spostare le forze lungo la loro retta d’azione. Applicarli al bordo o sulla superficie esterna è indifferente.
Per spostare invece i carichi tangenziali bisogna tenere conto dei momenti di trasporto.
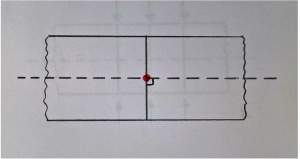
Possiamo quindi monitorare, tramite il nodo di controllo, le rototraslazioni rigide dell’elemento corrispondente. Modellando l’elemento piastra attraverso i segmenti rigidi introdotti che vietano alcuni moti di deformazione (ad es. strizione) rendiamo la piastra più rigida.
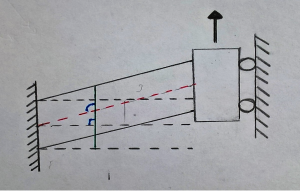
Dato un oggetto tipo piastra e riconosciuto il suo piano medio, la modellazione ora introdotta produce errori non tollerabili per elementi con brusche variazioni di spessore. Il modello adottato produce un errore maggiore all’aumentare dello spessore della piastra. Si può applicare solo per piastre accettabilmente sottili rispetto all’estensione del piano medio. Introdotta una soglia per cui è tollerabile l’errore (relativa al rapporto tra spessore e una dimensione caratteristica), si può considerare accettabilmente sottile la piastra. Non esiste una soglia generale per l’applicabilità della teoria. Data ad esempio una piastra forata, con foro circolare di diametro (d), per l’applicabilità della teoria bisogna confrontare le dimensioni del diametro del foro e le dimensioni della piastra. Dovendo valutare la rigidezza locale della piastra, confronto il diametro con lo spessore (s) della piastra poiché è interessante lo stato tensionale in prossimità del foro. Dovendo invece valutare la rigidezza globale della piastra, posso confrontare la larghezza (w) della piastra con lo spessore (s) senza tenere conto del foro.
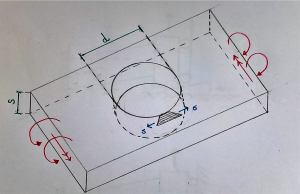 [Non è possibile applicare la teoria della piastra se lo spessore (s) e il diametro (d) sono dello stesso ordine di grandezza]
[Non è possibile applicare la teoria della piastra se lo spessore (s) e il diametro (d) sono dello stesso ordine di grandezza]
Superficie superiore e inferiore possono essere assegnate in maniera arbitraria. Superficie media è dove posiziono i nodi per controllare la rototraslazione dei segmenti.
I nodi di controllo posso essere spostati arbitrariamente lungo z, definisco quindi la superficie di riferimento, quella in cui posiziono i nodi di controllo e solitamente coincide con la superficie media. Gli oggetti piani sono definiti tali se la superficie media è piana (plates). Se la superficie media non è piana sono gusci (shell).
Lastra è un oggetto sottile piano, caricato entro piano. Piastra è un oggetto sottile piano, caricato fuori piano.
Teoria di Kirchhoff per piastra sottile e teoria di Reissner-Mindlin
La Teoria di Kirchhoff della piastra sottile ipotizza che i punti appartenenti a segmenti rettilinei normali al piano medio prima della deformazione, si trovino ancora su un segmento rettilineo normale, localmente, alla superficie a deformazione avvenuta. L’interpretazione fisica consiste nel considerare trascurabili gli scorrimenti $\gamma_{xz}$ e $\gamma_{yz}$.
Tengo conto solo di deformazioni flessionali e membranali, escludendo quelle a taglio fuori piano. Non considerare le deformazioni a taglio, non vuol dire che non esistono sforzi di taglio. Essi non causano variazioni di energia potenziale elastica non essendoci deformazioni associate.
La Teoria di Reissner-Mindlin contempla la deformazione tagliante.
Secondo Kirchhoff , presa una piastra sottile indeformata e considerati i segmenti normali alle superficie di riferimento, a seguito di una flessione dell’elemento tutti i segmenti rimangono sempre perpendicolari al piano medio (caso di deformazione puramente flessionale).
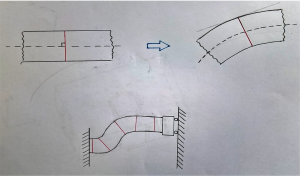
Per Reissner-Mindlin possiamo considerare una piastra tozza così vincolata :
Nel caso di deformazione flesso-tagliante i segmenti non rimangono perpendicolari al piano medio poiché questo ruota mentre il segmento trasla verso l’alto. A seguito dello spostamento verticale del carrello non si conserva l’ortogonalità del segmento rispetto al piano medio.
La teoria di Kirchhoff commette errori notevoli se la piastra è tozza mentre quella di Reissner-Mindlin rimane ancora valida. Per rapporti spessore/lunghezza caratteristica intorno a $\frac{1}{20}$ possiamo affrontare il problema con Kirchhoff, se scendiamo a valori di ⅛ , ⅙ , o ¼ è necessario ricorrere alla teoria di Reissner-Mindlin.
Thin shell → teoria di Kirchhoff: le tensioni del taglio non sono nulle ma trascurabili, vengono perciò escluse.
Thick shell → teoria di Reissner-Mindlin: include le deformazioni a taglio.
Una piastra alla Kirchhoff può deformare a taglio solamente se il carico tagliante è entropiano. $$ \gamma_{xy}=\frac{\tau_{xy}}{G} $$
$$ \gamma_{zx}=\gamma_{yz}=0 $$
Per semplificare la trattazione, oltre a non considerare elementi shell, introduciamo l’ipotesi di piccoli spostamenti e in particolare piccole rotazioni. Tale ipotesi ci permette di semplificare tramite lo sviluppo di Taylor ottenendo una forma lineare per le equazioni dell’equilibrio.
$sin\vartheta\cong\vartheta , cos\vartheta\cong\vartheta , tan\vartheta\cong\vartheta$
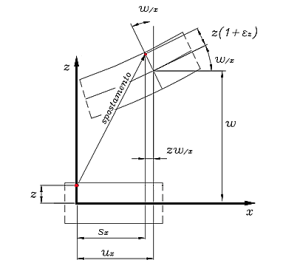
Per ogni generico punto P relativo alla piastra (di materiale elastico), possiamo considerare la sua proiezione Q sul piano medio. Lo spostamento W (lungo z) associato al punto sarà uguale a quello proiettato sul piano medio. I punti che nascono allineati sullo stesso segmento hanno lo stesso spostamento w lungo z perciò ogni spostamento w del punto P equivale allo spostamento Q del punto preso sulla superficie di riferimento.
$$ W = W (x,y) $$
w non è funzione di z, invece, le componenti degli spostamenti u e v del punto P e della sua proiezione non concidono.
Considero le rotazioni $\varphi_{x}$ e $\varphi_{y}$. Si può chiamare una rotazione $\varphi_{x}$ perché x è l’asse nel quale la rotazione produce uno spostamento apprezzabile, interessante perciò da studiare.
Gli spostamenti del punto P sono definiti in funzione della deformazione del punto sul piano medio:
$u = u_{0} - z\frac{dw_{0}}{dx}$; $v = v_{0} - z\frac{dw_{0}}{dy}$; $W = W (x,y)$
Possiamo definire le deformazioni del punto P:
$$\varepsilon_{x} = \frac{du}{dx} = \varepsilon_{x0} - z\frac{dw^2_{0}}{dx^2}$$
dove $\frac{dw^2_{0}}{dx^2}$ è la curvatura flessionale (ottenuta spostandoci lungo x)
$$\varepsilon_{y} = \frac{dv}{dy} = \varepsilon_{y0} - z\frac{dw^2_{0}}{dy^2}$$
dove $\frac{dw^2_{0}}{dy^2}$ è la curvatura flessionale (ottenuta spostandoci lungo y)
$$\gamma_{xy} = \frac{du}{dx} + \frac{dv}{dy} = \gamma_{xy} -2z\frac{dw^2_{0}}{dxdi}$$
dove $\frac{dw^2_{0}}{dxdi}$ è la curvatura torsionale
con $W_{0}$ intendiamo lo spostamento di Q lungo z nel piano di riferimento, indicato con 0.
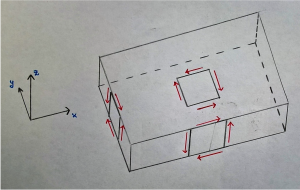
Per valutare la curvatura torsionale consideriamo un piano di riferimento (avremo del materiale sia superiormente che inferiormente) di questo tipo:
Campionando la struttura con un sistema di riferimento così assunto potremo valutare una curvatura di tipo torsionale. Se gli spostamenti sono uguali in modulo otterremo una deformata come quella evidenziata in figura, il segmento equidistante dagli estremi non compirà alcuna rotazione. Spostandoci da questo segmento verso gli estremi del piano, possiamo quindi valutare la curvatura torsionale poiché questa sarà pari alla variazione di rotazione lungo x ed y della deformata rispetto all’indeformata.
Si definisce la colonna delle deformazioni del punto P come:
${\varepsilon (x,y)}={\varepsilon_{0}(x,y)} +z{k(x,y)} $
dove ${\varepsilon_{0}(x,y)}$ sono le deformazioni membranali del piano medio e ${k(x,y)}$ definisce la curvatura del piano medio, in particolare si hanno due componenti di flessione e una torsionale. Il termine $\gamma_{xy}$,dato dalla somma delle due derivate parziali degli spostamenti $(\frac{du}{dy} + \frac{dv}{dx})$, corrisponde ad una deformazione tagliante entropiano che deve essere diversa da zero nella teoria di Kirchoff.
[Gli spostamenti così definiti comportano la deformazione rotazionale della piastra.]
Una volta definite le deformazioni devo determinare le tensioni, se avessimo $(\varepsilon_{z}=0)$ saremmo nel caso di deformazione piana ma perchè questa relazione sia verificata ho bisogno che le $\sigma _{z}$ siano diverse da zero per poter contrastare l’effetto Poisson. Tipicamente queste tensioni sono nulle.
Per il modello cinematico vorrei che le deformazioni lungo z fossero nulle così il corpo che nasce rigido rimane tale , ma per l’ipotesi di $(\gamma_{yz}=0)$ si ha che la deformazione è libera lungo z. Adottiamo quindi un approccio misto per quanto riguardo il legame cinematico $(\varepsilon_{z}=0)$, ossia quel segmento rimane rigido, però prendo il legame tensione-deformazione per ogni segmento in tensione piana, ovvero con $(\varepsilon_{z}\neq0)$ e $\sigma _{z}=0$ dove avremo che:
$\varepsilon_{z}=-\nu(\varepsilon_{x}+\varepsilon{y})$
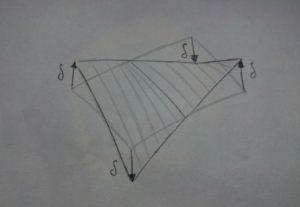
Prendendo in considerazione una piastra costituita da due fette di materiale, osserviamo la deformata e l’indeformata :
A seguito di una trazione, osserveremo uno spostamento macroscopico lungo x e un allungamento della sezione. In particolare la fettina di materiale considerato andrà in strizione lungo z.
Per immaginare il comportamento della piastra possiamo pensare che vi sia discontinuità degli spostamenti fra fettina e fettina, così che due punti su di un segmento non possano avvicinarsi e questo possa rimanere macroscopicamente rigido così da soddisfare la cinematica. Ogni fettina può, inoltre, andare in strizione in modo da soddisfare la condizione di tensione piana così da avere $\sigma _{z}=0$.
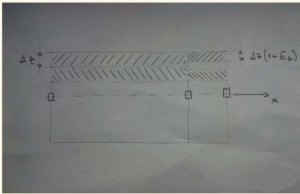
Si può analizzare lo spessore della piastra suddividendolo in 3 elementi, se si sposta il solo nodo centrale tutto l’elemento si allunga in direzione x mentre il suo spessore diminuisce di $\Delta z(1+\varepsilon_{z})$. Tuttavia non possiamo ammettere la contemporanea valenza del modello cinematico, della tensione piana e dell’ipotesi di continuità degli spostamenti lungo lo spessore. Trascuriamo la più innocua che è appunto quest’ultima ammettendo che si aprano dei tagli o si abbiano delle discontinuità tra uno strato di piastra e il successivo.
Per potermi trovare nel caso in cui valgano entrambe le ipotesi devo considerare una piastra costituita da più fette libere di andare in strizione indipendentemente dalle altre. Volendo ottenere lo spessore della piastra basterà sommare i singoli spessori delle fette.
Tabella di monitoraggio carico orario
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Biconne Francesco | 9 | — | — | — | 9 |
| Cerisara Alberto | 9 | — | — | — | 9 |
| Mariottini Ludovico | 9 | — | — | — | 9 |
| Pietrolati Luca | 9 | — | — | — | 9 |
| Revisore 1 | — | — | — | — | – |
| Revisore 2 | — | — | — | - | - |
| Revisore 3 | — | — | — | — | - |
| Revisore 4 | — | — | — | — | — |
| Totale | - | —- | —- | - | — |
</hidden>