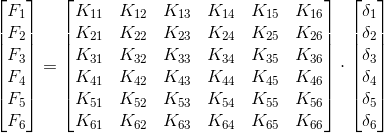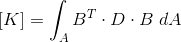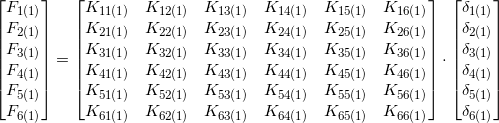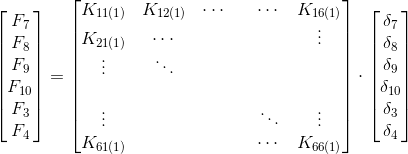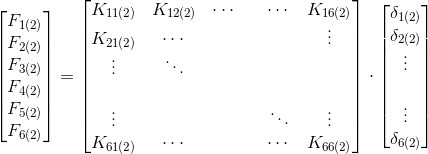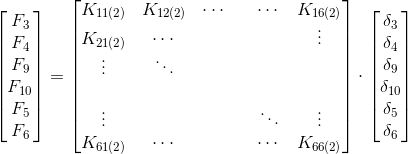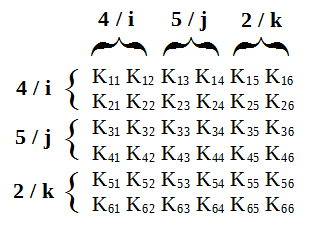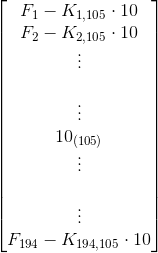Continuazione Elemento Triangolare
Argomenti lezione
- Riassunto lezione precedente
- Assemblaggio matrici
- Definizione scrittura locale e globale
Riassunto Lezione
Nella lezione precedente si è visto come si costruisce la matrice di rigidezza tramite il Principio dei Lavori Virtuali, partendo da un elemento finito triangolare i cui nodi seguono la numerazione i,j,k o 1,2,3 e attraverso una definizione a priori del campo degli spostamenti all'interno dell'elemento, visto anche come
- Spostamento in x di un punto generico U(x,y) = N1(x,y)U1 + N2(x,y)U2 + N3(x,y)U3
- Spostamento in y di un punto generico V(x,y) = N1(x,y)V1 + N2(x,y)V2 + N3(x,y)V3
ovvero come combinazioni lineari delle funzioni di forma degli spostamenti nodali (funzioni scelte ad arbitrio). Dopodichè, svolgendo gli opportuni passaggi e le opportune integrazioni, si è giunti alla definizione della matrice di rigidezza K.
Gli spostamenti sopra rappresentati, avendo scelto a priori il campo degli spostamenti all’interno dell’elemento, rappresentano il “cuore” dell’elemento finito: infatti, se il campo degli spostamenti è lineare, ci si aspetta che lo stato tensionale sia costante, poiché la deformazione è costante e, di conseguenza, se il materiale è isotropo lineare, risulterà costante anche lo stato tensionale. Quindi, all’interno dell’elemento rappresentato, il campo deformativo è costante e lo stato tensionale è costante.
È necessario ricordare che l’unica teoria esatta è la Teoria dei Tubi, dove lo stato tensionale è 1/R2.
Nel campo xy (oppure utilizzando le coordinate polari) lo stato tensionale non è lineare: se si studia un tubo agli elementi finiti usando l’elemento triangolare in sezione piana, lo stato nella sezione è costante e non si possono vedere gli stati massimi e minimi ma solo i valori medi. L’utilizzo dell’elemento più idoneo per la nostra applicazione è a libera scelta.
Fatta questa assunzione, è stato possibile scrivere quanto segue:
dove:
- la matrice delle Fi rappresenta la matrice delle forze nodali
- la matrice delle Kij rappresenta la matrice di rigidezza
- la matrice delle δi rappresenta la matrice degli spostamenti (δ = spostamento generico) identificando con gli spostamenti dispari quelli lungo x e gli spostamenti pari lungo y
Attraverso l’uguaglianza tra il lavoro virtuale interno e il lavoro virtuale eterno è possibile scrivere la matrice di rigidezza K:
dove:
- B: matrice che lega le ε alle U. Nel piano si ottiene dalle derivate parziali di U, con le U scelte ad arbitrio: quindi, che la matrice B sia costante o una funzione, dipende da come sono state scelte le funzioni di forma. Essendo delle derivate rispetto a x o y incrociate, con εx derivata parziale di U rispetto a x, se U fosse lineare in x si otterrebbe εx costante e se U non fosse lineare in x ma di 2° grado, εx sarebbe una funzione, dunque variabile all’interno dell’elemento.
- D: matrice che lega le ε alle σ (vista a lezione solo per materiali isotropi, omogenei e lineari). Viene identificata da due soli parametri: Modulo di Young E e coefficiente di Poisson ν (se fosse ortotropa cambierebbe).
Questa matrice contiene il cuore del materiale ed è complicabile a piacimento inserendo diversi parametri nella matrice.
Come già visto la matrice B si ottiene da U(x,y): α1 + α2x + α3y
La derivata di questa funzione rispetto a x forniva come risultato εx = α2 con α2 che era funzione solamente delle coordinate nodali. La soluzione degli αn con n=1,…,6 fornisce la soluzione per i 3 nodi con 6 g.d.l.
Se si arricchisse con
U(x,y) = … + α7x2
V(x,y) = … + α8y2
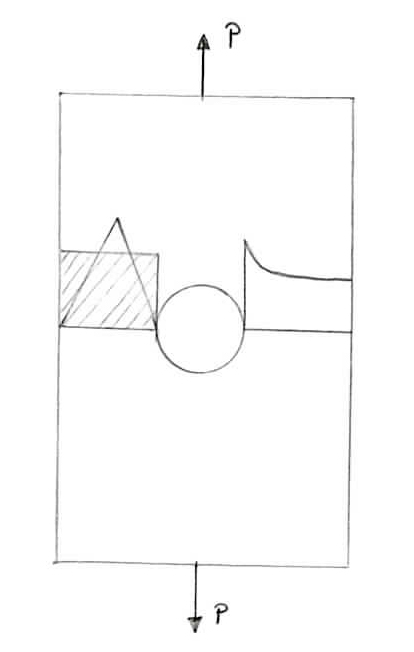
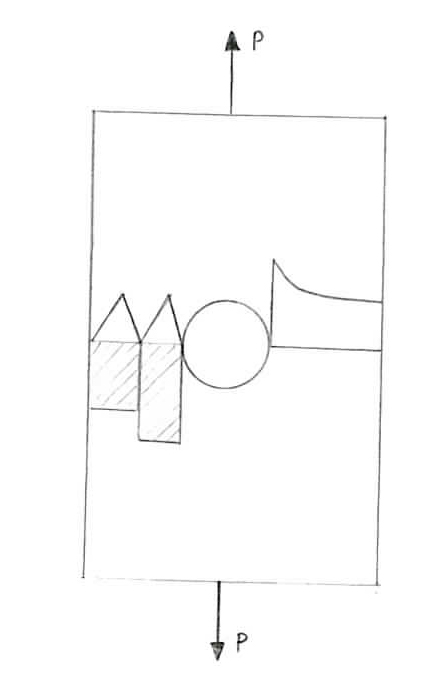
si dovrebbe aggiungere un nodo, magari al centro. Ciò giustifica la presenza di triangoli a tre nodi o triangoli a sei nodi, conseguenza del fatto che vengono arricchite le funzioni di forma U,V. Avere funzioni di forma diverse non dà soluzioni esatte o meno ma semplicemente forniscono spostamenti in x o y con gradi diversi. Se la funzione di forma avesse un grado superiore, si otterrebbe un’equazione di ε e σ diversa, non più costante o lineare ma di grado superiore. Triangoli di questo tipo, con stato tensionale costante, più piccoli sono, più vicina sarà la soluzione che danno rispetto alla soluzione reale. Facciamo un esempio. Foro in una lastra forata sottoposta a trazione
È noto che il valore massimo dello stato tensionale si trova sul bordo del foro, in corrispondenza della sezione minima perpendicolare al carico con l’andamento rappresentato in figura (lato destro). Si osservi il caso in cui venga utilizzato un elemento finito triangolare per rappresentare lo stato tensionale. Lo stato tensionale dell’elemento finito fornirà il valore medio costante dell’andamento reale poiché è costante l’elemento. Come output si ha che lo stato tensionale è quello rappresentato perché σ è costante e dovrà equilibrare il carico quindi sarà la tensione media: P/2*Sezione minima.
Si osservi ora il caso in cui vengano utilizzati due elementi finiti.
Lo stato tensionale reale è lo stesso del caso precedente, essendo la stessa lastra caricata allo stesso modo. È possibile osservare i due andamenti dello stato tensionale, uno leggermente sopra il valore medio e uno di poco sotto di esso, dove la media dei due stati tensionali rappresentati è lo stesso valore della media fornito da un unico elemento finito. E’ evidente l’analogia con l’integrale, che sia a trapezio o a rettangolo. L’approssimazione compiuta con un elemento finito triangolare è legata al fatto che si ha uno stato tensionale costante all’interno dell’elemento: perciò, più piccoli saranno gli elementi finiti, più si riuscirà a “prendere” i gradienti. Laddove vi è un gradiente molto forte di tensione, sarà necessario ridurre di dimensione gli elementi finiti (nell'esempio si tratta del bordo del foro in corrispondenza della sezione perpendicolare al carico) per poter ridurre l’errore. Se non vi fosse il foro nella lastra, si potrebbe utilizzare un unico elemento finito triangolare e la soluzione ottenuta sarebbe esatta. Dopo queste considerazioni, si intuisce che la scelta della funzione di forma vincola il modo in cui si opera sulla struttura; se si utilizza un elemento lineare (il triangolo a tre nodi è un elemento lineare così come il tetraedro nel 3D), lo stato tensionale al suo interno sarà costante. Si osservi ora un esempio pratico. Finora è stato possibile scrivere il problema in termini di forze e spostamenti all’interno di un unico triangolo (cioè un solo elemento finito) ma come si è visto dell’esempio precedente, non si utilizzerà mai un elemento unico per descrivere un corpo, ma sarà necessario eseguire una MESHATURA, ovvero creare un insieme di elementi triangolari. Si osservi nello spazio di lavoro x-y il caso di tre elementi triangolari.
Assemblaggio Matrici
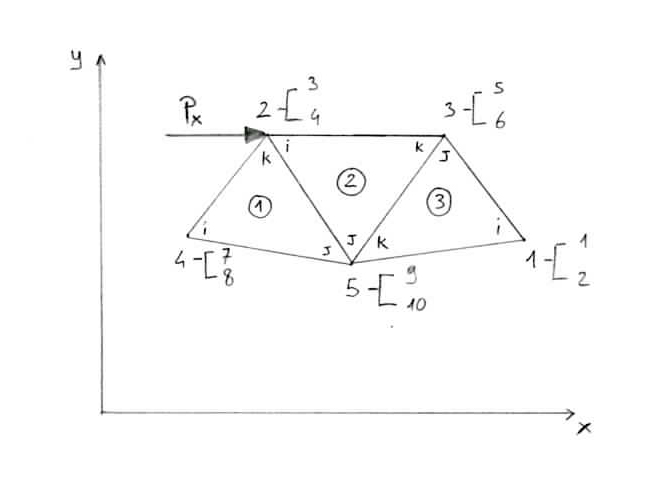 In questo caso la mesh si compone di tre elementi (quelli cerchiati), diversi dai nodi che vanno da 1 a 5, ovvero i vertici dei triangoli.
Ad ogni triangolo all’interno dello stesso è stata assegnata una nomenclatura, con circuitazione sempre destrorsa (antioraria), in modo da poter creare una normale positiva per far sì che la sua area, se calcolata automaticamente, fosse positiva. Con la numerazione inversa l’area può essere negativa ma, come si è visto, l’area fa parte della matrice di rigidezza nel legame tra spostamenti e deformazioni e, se fosse negativa, fornirebbe tutti valori negativi, creando dei problemi e assimilando il problema ad un elemento aghiforme.
In questo caso la mesh si compone di tre elementi (quelli cerchiati), diversi dai nodi che vanno da 1 a 5, ovvero i vertici dei triangoli.
Ad ogni triangolo all’interno dello stesso è stata assegnata una nomenclatura, con circuitazione sempre destrorsa (antioraria), in modo da poter creare una normale positiva per far sì che la sua area, se calcolata automaticamente, fosse positiva. Con la numerazione inversa l’area può essere negativa ma, come si è visto, l’area fa parte della matrice di rigidezza nel legame tra spostamenti e deformazioni e, se fosse negativa, fornirebbe tutti valori negativi, creando dei problemi e assimilando il problema ad un elemento aghiforme.
 Questo elemento ha un’area pressoché nulla e 1/A tende ad infinito, rendendo singolari i termini della matrice B. Ritorniamo al nostro problema.
Essendo noto il modo in cui scrivere la matrice di rigidezza per ogni elemento, per l’elemento 1 si avrà:
Questo elemento ha un’area pressoché nulla e 1/A tende ad infinito, rendendo singolari i termini della matrice B. Ritorniamo al nostro problema.
Essendo noto il modo in cui scrivere la matrice di rigidezza per ogni elemento, per l’elemento 1 si avrà:
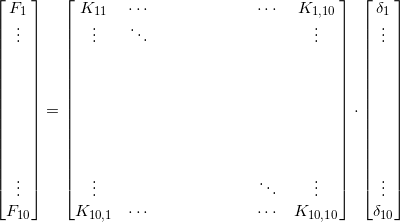
F1(1) e F2(1) sono le forze nodali al nodo 4 (i valori tra parentesi indicano l’elemento considerato); in particolare F1(1) è la forza in x del nodo i-esimo dell’elemento 1. Nel caso di elemento N le forze saranno F1(N). L’obiettivo è quello di scrivere tutti gli indici giusti di ogni singolo elemento andando successivamente ad inserirli in un’unica matrice dell’intera mesh, che sarà un problema di questo tipo:
La difficoltà consiste nell’inserire in maniera corretta il valore del singolo elemento nella matrice globale. Come si vede, se si ha una mesh con n nodi nel piano, si avrà una matrice di dimensione 2n x 2n; nel nostro caso i nodi sono 5 quindi la matrice sarà 10 x 10. Nel caso tridimensionale la matrice globale di una mesh con n nodi sarà di dimensioni 3n x 3n. La regola per passare da un globale ad un locale (pari lungo y e dispari lungo x) ha una numerazione globale ed è per questo che si parlerà sempre di numerazione globale. Si associa allo spostamento lungo x la numerazione 2n-1 con n il numero del nodo di numerazione globale e lo spostamento lungo y la numerazione 2n: ciò significa che per il nodo 4 globale si avranno due spostamenti indicizzati nella matrice globale come:
lungo x: 2*4-1=7 / lungo y: 2*4=8
Otterremo quindi per il nodo 4:
x) F7 δ7 y) F8 δ8
…e così via per tutti i nodi della mesh. Dunque, è possibile riscrivere la matrice dell’elemento 1 non più con la numerazione locale ma con la numerazione globale, in quanto la numerazione globale prevale sulla locale, detta anche regola di assemblaggio. Si osservino ora, sempre per l’elemento 1, le matrici di forze e spostamenti con la numerazione globale.
F1(1): forza lungo x del nodo i-esimo dell’elemento 1, nonché nodo 4 della mesh; F1(1) = F7
F2(1): forza lungo y del nodo i-esimo dell’elemento 1, nonché nodo 4 della mesh; F2(1) = F8
F3(1): forza lungo x del nodo j-esimo dell’elemento 1, nonché nodo 5 della mesh; F3(1) = F9
F4(1): forza lungo y del nodo j-esimo dell’elemento 1, nonché nodo 5 della mesh; F4(1) = F10
F5(1): forza lungo x del nodo k-esimo dell’elemento 1, nonché nodo 3 della mesh; F5(1) = F3
F6(1): forza lungo y del nodo k-esimo dell’elemento 1, nonché nodo 3 della mesh; F6(1) = F4
Per i Kij non si procede allo stesso modo poiché, ad esempio, F10 può essere scritto anche come elemento 2 dato che il nodo j dell’elemento 2 corrisponde al nodo 5 della numerazione globale. Sarà, quindi, la combinazione dei contributi di tutti gli elementi della mesh che andranno a comporre la matrice di rigidezza globale. Procediamo ora nella determinazione dell’equilibrio del nodo 2, il quale avrà una parte derivante da F3 ottenibile considerando sia l’elemento 1 che l’elemento 2 e dovrà eguagliare Px. Sia fissata la matrice di rigidezza dell’elemento 1. Analogamente, si può procedere con l’elemento 2. Sulla base della conoscenza della matrice di rigidezza di ogni singolo elemento della mesh, si vuole scrivere il problema nella sua forma globale. Successivamente, una volta scritta la mesh nella forma globale, si risolverà nei vari modi noti:si tratta di un problema lineare con incognite (spostamenti δ), termini noti (forze F) dove la matrice di rigidezza è nota perché la mesh è scelta dall'utente in funzione del materiale scelto. Dagli spostamenti δ si andranno a calcolare in cascata ε e σ. E’ per questo motivo che i problemi agli elementi finiti si dicono “problemi agli spostamenti” perché gli spostamenti δ sono le incognite primarie. Che il problema sia lineare o meno o che le tecniche di soluzione numerica siano adatte o meno dipende dalla tipologia di problema: se si hanno problemi lineari è possibile invertire la matrice e risolverla direttamente oppure risolverla con il metodo iterativo di Gauss ecc. Una volta noti gli spostamenti, tutto risulta noto poiché, note le funzioni di forma imposte arbitrariamente, è possibile risalire agli spostamenti di tutti gli elementi finiti e da lì calcolare ε e σ.
Matrice dell’elemento 2 con scrittura locale
Matrice dell'elemento 2 con la numerazione globale
Si osservi ora l’equilibrio del nodo 2 lungo x, che si può vedere come appartenente all’elemento 1 e all’elemento 2. Si avrà quindi una forza derivata dall’elemento 1, ovvero una F3 derivata dall’elemento 1, e una forza derivata dall’elemento 2, sempre F3. La forza agente sul nodo 2 sarà la risultante delle due forze che andrà ad equilibrare la forza P. Si analizzi il nodo 2 visto dall’elemento 1 e si consideri solo le forze derivanti dall’elemento 1; nel nostro caso, vi è solamente F3(1) (=F3’), derivante dal prodotto della penultima riga della matrice di rigidezza per la colonna degli spostamenti. Si ottiene, quindi:
F3’= K51(1)δ7 + K52(1)δ8 + K53(1)δ9 + K54(1)δ10 + K55(1)δ3 + K56(1)δ4
Analizziamo ora il nodo 2 visto dall’elemento 2, ottenuto dal prodotto tra la prima riga della matrice di rigidezza per la colonna degli spostamenti. Otteniamo quindi:
F3’’= K11(2)δ3 + K12(2)δ4 + K13(2)δ9 + K14(2)δ10 + K15(2)δ5 + K16(2)δ6
Sul nodo 2 la forza agente sarà la somma delle due forze, ovvero il contributo dell’elemento 1 sommato al contributo dell’elemento 2:
F3 = F3’ + F3’’= δ3 (K55(1) + K11(2)) + δ4 (K56(1) + K12(2)) + δ5 K15(2) + δ6 K16(2) + δ7 K51(1) + δ8 K52(1) + δ9 (K53(1) + K13(2)) + δ10 (K54(1) + K14(2))
È importante osservare che l’elemento 3 non influisce sull’equilibrio del nodo 2.
Inseriamo F3 nella matrice globale:
 (gli elementi non segnati sono indeterminati)
(gli elementi non segnati sono indeterminati)
Per capire come inserire in maniera rapida tutti i termini all’interno della matrice di rigidezza, si osservi l’elemento 1:
Definizione scrittura locale e globale
Nella numerazione globale, l’elemento 1 assume i seguenti valori:
- i = 4
- j = 5
- k = 2
Si ricorda che la regola dell’assemblaggio prevede di associare allo spostamento lungo x la numerazione 2n-1 (dove n è il numero del nodo di numerazione globale) e allo spostamento lungo y la numerazione 2n. Dunque:
- i = 4 : 7 - 8
- j = 5 : 9 - 10
- k = 2 : 3 - 4
Seguendo questa regola e con l’aiuto dell’immagine, è possibile citare alcuni esempi:
- K55 diventerà K33 nella numerazione globale;
- K12 diventerà K78 nella numerazione globale;
- K23 diventerà K89 nella numerazione globale;
- K54 diventerà K310 nella numerazione globale.
È bene ricordare che per comporre tale numerazione è necessario scrivere prima l’indice di riga e poi l’indice di colonna associato all’elemento Kab. Ad esempio:
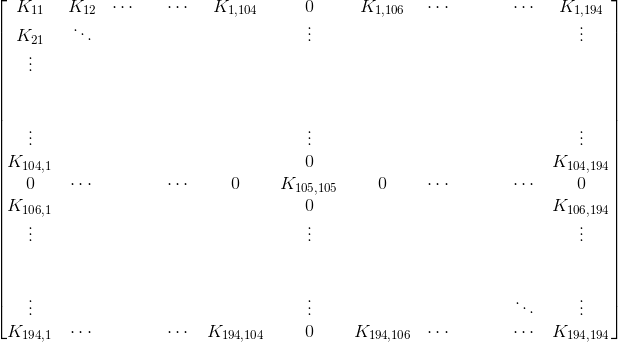
Attenzione: Se la matrice fosse piena di elementi, si dovrebbero fare troppi calcoli. Ad esempio, per analizzare un crash test completo vengono spese dalle 24 alle 48 ore, nonostante i dati vengano elaborati da più computer che lavorano in parallelo. Dunque, si ha interesse a rendere alcuni elementi nulli, senza toccare gli elementi diagonali i quali rimarranno sempre diversi da zero. La matrice ottenuta sarà sempre simmetrica e semidefinita positiva e ciò la renderà non invertibile poiché il suo determinante è nullo. Il fatto che la matrice sia simmetrica e semidefinita positiva ha un significato fisico: dal punto di vista statico, il problema non è risolvibile poiché non vi sono vincoli. Si nota, infatti, che la forza Px applicata sposta gli elementi 1,2 e 3.
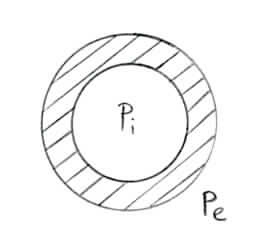
Si può fare un ragionamento analogo anche nel caso di un tubo in pressione con risultante nulla:
Pi = pressione interna
Pe = pressione esterna
Entrambe le pressioni agiscono su volumi chiusi e generano “spostamenti deformativi” a meno di spostamenti rigidi, ovvero deformano il tubo (“spostamento deformativo”) in egual modo ovunque si trovi il tubo nello spazio dimensionale. Questa situazione non è risolvibile al FEM poiché la struttura non risulta vincolata.
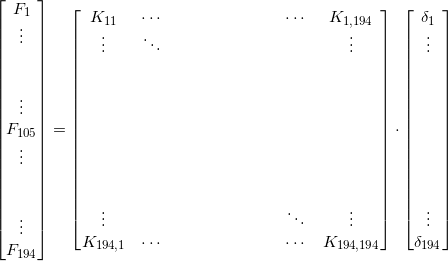
Dunque, come si vincola una struttura dal punto di vista matriciale? Quando si inserisce un carrello od una cerniera in una struttura, si impone che lo spostamento in un determinato punto della struttura stessa sia uguale a zero. Si consideri una mesh con 97 nodi (194 gradi di libertà):
Immaginiamo di vincolare 1 g.d.l., ovvero di rendere nullo uno spostamento: δ105. Non è possibile porre immediatamente δ105 = 0 perché la matrice rimarrebbe semidefinita positiva, quindi irrisolvibile. Dunque, è necessario far sì che δ105 diventi nullo nel calcolo della soluzione del problema. Scriviamo F105:
F105 = δ1K105,1 + δ2K105,2 + … + δ105K105,105 + … + δ194K105,194
Ora, si annullino tutti i termini K della riga 105 tranne il termine K105,105, il quale viene posto uguale a 1:
K105,105 = 1
Inoltre, si ponga F105 = 0. In questo modo, si ottiene:
0 = δ105 * 1
L’obbiettivo è stato raggiunto poiché ora δ105 = 0. Così facendo, però, si è persa la simmetria della matrice. Per ripristinare la simmetria, dovrei annullare anche tutti gli elementi della colonna che contiene K105,105:
È possibile annullare tutti gli elementi della colonna 105 (tranne l’elemento diagonale) poiché è stato imposto δ105 = 0 quindi Kn,105 δ105 = 0 (n = 1, … , 194) da cui Kn,105 = 0. Si analizza ora il caso di vincolo cedevole, imponendo δ105 = 10:
Si pone F105 = 10, si annullano tutti i termini K105,n (tranne il termine K105,105 che è uguale a 1) e si ottiene:
10 = 1 * δ105 In questo caso non è possibile annullare i termini della colonna 105 poiché, ad esempio:
F1 = K11δ1 + … + K1,105δ105 + … + K1,194δ194
Se si annullasse K1,105 , si perderebbe il contributo di K1,105 δ105. Infatti si avrebbe: K1,105 δ105 = 0 * 10 (è possibile estendere il ragionamento a tutti i termini della colonna 105). Per evitare questo problema, si portano a sinistra i vari termini Kn,105 * 10 (n = 1, … , 194):
È necessario prestare attenzione alla riga 105:
K105,105 * 10 = 1 * 10 = 10
Va inserito il numero 10 e non K105,105 * 10 !
Autori
Stefano Codognotto, Andrea Hawila, Michele Pagura, Nicolò Salgaro.
Tabella di monitoraggio carico orario
Ore-uomo richieste per la compilazione della pagina.
| Autore/Revisore | Prima stesura | Prima revisione | Seconda stesura | Revisione finale | Totale |
|---|---|---|---|---|---|
| Codognotto | 6 | — | — | — | 6 |
| Hawila | 6 | — | 0.5 | — | 6.5 |
| Pagura | 6 | — | — | — | 6 |
| Salgaro | 6 | — | — | — | 6 |
| Revisore 1 | — | 0.75 | — | — | 0.75 |
| Revisore 2 | — | — | — | — | — |
| Revisore 3 | — | — | — | — | — |
| Revisore 4 | — | — | — | — | — |
| Totale | 24 | 0.75 | 0.5 | — | 25.25 |