Indice
plate_from_stresses_to_resultants.pdf
four_point_bending_pstrain_v000.pdf
LEZIONE 13
A cura di Marco Tambara e Nicolò Vincenzi
Prova a flessione a 4 punti
La prova a flessione a 4 punti consiste nel caricare una piastra appoggiata su due appoggi con due carichi come in figura. Si rileva inoltre che la struttura è simmetrica e di conseguenza se ne studia solo una metà.

 Consideriamo un campione della piastra nella zona intermedia della stessa, evidenziato in figura in rosso.
Il caricamento comporta la sollecitazione flessionale pura nel campione, che in modulo vale $M_f=F\cdot l$, in cui $l$ è la distanza del punto di applicazione di una delle due forze dall'appoggio più vicino. Considerando la figura, si può definire il flusso delle tensioni in direzione $x$, $y$ e $z$:
\begin{align}
m_x=&\ \frac{F l}{b}=\int_h \sigma_x z\, dz\\
m_y=&\ 0\\
m_{xy}=&\ 0
\end{align}
Ipotizzando il materiale isotropo e omogeneo, si può scrivere il sistema di 3 equazioni in 3 incognite ($k_x$, $k_y$ e $k_{xy}$):
\begin{equation}
\underline{\underline{C}}\, \underline{k}=\underline{m}
\end{equation}
e considerando che $\underline{\underline{C}}=\frac{h^3}{12}\, \underline{\underline{D}}$, il sistema diventa:
\begin{equation}
\frac{h^3}{12}\, \underline{\underline{D}}\, \underline{k}=\underline{m}
\end{equation}
Risolvendo in Maxima, con $m_x=\frac{F l}{b}$, $m_{xy}=0$ e $m_y=0$:
\begin{align}
k_x=&\ \frac{12 l F}{b h^3 E}\\
k_y=&\ -\frac{12 l \nu F}{b h^3 E}= - \nu\, k_x
\end{align}
Consideriamo un campione della piastra nella zona intermedia della stessa, evidenziato in figura in rosso.
Il caricamento comporta la sollecitazione flessionale pura nel campione, che in modulo vale $M_f=F\cdot l$, in cui $l$ è la distanza del punto di applicazione di una delle due forze dall'appoggio più vicino. Considerando la figura, si può definire il flusso delle tensioni in direzione $x$, $y$ e $z$:
\begin{align}
m_x=&\ \frac{F l}{b}=\int_h \sigma_x z\, dz\\
m_y=&\ 0\\
m_{xy}=&\ 0
\end{align}
Ipotizzando il materiale isotropo e omogeneo, si può scrivere il sistema di 3 equazioni in 3 incognite ($k_x$, $k_y$ e $k_{xy}$):
\begin{equation}
\underline{\underline{C}}\, \underline{k}=\underline{m}
\end{equation}
e considerando che $\underline{\underline{C}}=\frac{h^3}{12}\, \underline{\underline{D}}$, il sistema diventa:
\begin{equation}
\frac{h^3}{12}\, \underline{\underline{D}}\, \underline{k}=\underline{m}
\end{equation}
Risolvendo in Maxima, con $m_x=\frac{F l}{b}$, $m_{xy}=0$ e $m_y=0$:
\begin{align}
k_x=&\ \frac{12 l F}{b h^3 E}\\
k_y=&\ -\frac{12 l \nu F}{b h^3 E}= - \nu\, k_x
\end{align}
programma maxima
Questo significa che è presente una curvatura anche in direzione $y$, che non dovrebbe essere permessa dagli appoggi.
Si realizza però, che per via della curvatura in y si che i punti di contatto tra appoggi e piastra inizialmente erano dei segmenti, ma ora sono diventati dei singoli punti.
Si nota quindi come, grazie a questa nuova configurazione di applicazione, le forze tendano a ridurre la curvatura $k_y$. Tale curvatura però non si annullerà mai completamente in modo autonomo, bensì dovrebbero essere applicate due coppie agli estremi della piastra, come rappresentato in figura:
questo fatto è però in contrasto col tipèo di vincolo. Questi appoggi non potrebbero trasmettere un momento. Si deve però considerare il risultato “sperimentele” che vede il raddrizzarsi della piastra, quando sottoposta a schiacciamento. Questo implica che $m_y\neq\,0$ e $k_y=0$. Bisogna quindi aggiornare la soluzione del problema su Maxima considerando questa seconda opzione. In queste condizioni si ammette quindi che i vincoli possano trasmettere un certo momento $m_y=m_x\,\nu$ che rende nulla la curvatura in y, $k_y$
programma aggiornato
Risultati analisi con Elementi Finiti
Di seguito sono riportati nuovamente lo schema del problema in esame e i relativi risultati dell'analisi agli elementi finiti. I due grafici sono relativi rispettivamente ad un contatto bilaterale e un contatto unilaterale. Si nota inoltre che il termine $\nu m_x$ non è altro che il termine $m_x$ scalato col valore di $\nu$.
Analizzando il caso bilaterale si ha che la curvatura in y $k_y$ nel punto dell' appoggio, ad ascissa pari a 3, è nullo. Questo però è stato ottenuto forzando il contatto che in realtà è unilaterale e non bilaterale. Il secondo grafico mostra appunto questo risultato. si ha che per la natura del contatto vi è un gioco variabile $g(y)$ lungo la direzione y dovuto alla curvatura $k_y$. Si introduce quindi la condizione di Signorini. $$ P(y)\ g(y)=0$$ In questa relazione compaiono il suddetto gioco e la pressipone di contatto $P(y)$ e sta a indicare che dove il gioco non è nullo lo deve essere la pressione e viceversa. Di conseguenza si ha una non linearità dovuta all' inversione del carico e quindi la curvatura $k_y$ sull' appoggio, cioè ad ascissa 3, non è nulla.
Teoria degli elementi finiti
 La teoria degli elementi finiti consiste nella caratterizzazione attraverso elementi, i quali hanno diverse proprietà. Un primo elemento di vasto impiego è l'elemento piastra quadrilatero a 4 nodi.
La teoria degli elementi finiti consiste nella caratterizzazione attraverso elementi, i quali hanno diverse proprietà. Un primo elemento di vasto impiego è l'elemento piastra quadrilatero a 4 nodi.
Questo rappresenta una porzione di materiale che si comporta coerentemente con i suoi gdl e si oppone alla deformazione linearmente. Sull'elemento si definisce una funzione di interpolazione, la quale permette, noti gli spostamenti dei nodi, di ricavare gli spostamenti di un qualsiasi punto dell'elemento.
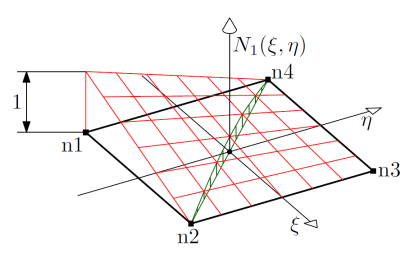
I nodi sono i vertici del quadrilatero, e in questi punti la funzione è definita: $f_1$, $f_2$, $f_3$ e $f_4$.
La funzione di interpolazione è $$ f_p=f_1 N_1(\xi,\eta) + f_2 N_2(\xi,\eta) + f_3 N_3(\xi,\eta) + f_4 N_4(\xi,\eta) $$ dove per ogni $\xi$ e $\eta$, $\sum_i N_i (\xi,\eta)=1$. Il valore di $N_j (\xi_i,\eta_i)$ deve essere 1 se $i=j$, 0 se $i\neq j$.
Per la definizione di $N$, si cerca una funzione continua e derivabile: i polinomi, con grado più basso possibile, sono adatti in quanto semplici da manipolare. Si scrive quindi $N_j$ evitando il termine quadratico $\xi^2$:
$$
N_j=a_j+b_j\, \xi + c_j\, \eta+d_j\, \xi \eta
$$
Per ricavare i coefficienti si impone, per esempio nel vertice 1, che $N_1=1$ ($\xi=-1$ e $\eta=-1$) e negli altri 0. In questo modo si ottiene $a=b=c=d=\frac{1}{4}$:
$$
N_1=\frac{1}{4}\left( 1-\xi\right)\left( 1-\eta\right)
$$
Da questo si può osservare che $N=\frac{1}{4}$ al centro del quadratino, 1 nel primo vertice e 0 negli altri vertici. Quindi non è una retta lungo la direzione che congiunge i vertici 2 e 4.
Invece, mantenendo $\xi$ costante $N_j$ è lineare in $\eta$ e viceversa. Questo andamento è detto bilineare. L'andamento bilineare è importante perché se si bloccano tutte le variabili tranne una, e l'unica libera è bilineare, allora sui 4 lati del quadrato il suo andamento è lineare.
Derivate parziali in $\xi$ e $\eta$
La funzione peso è derivabile: $$ \frac{\partial f}{\partial \xi}= \sum_i f_i \frac{\partial N_i}{\partial \xi} $$ $$ \frac{\partial f}{\partial \eta}= \sum_i f_i \frac{\partial N_i}{\partial \eta} $$ Dunque le derivate sono $$\frac{\partial f}{\partial \xi}= d \eta + b$$ e $$\frac{\partial f}{\partial \eta}= c \xi + d$$ La prima è bilineare in $\eta$ e costante in $\xi$, mentre la seconda è bilineare in $\xi$ e costante in $\eta$.



