Indice
Lezione 11
A cura di Nicolò Vincenzi e Marco Tambara
Consideriamo una piastra infinita avente un foro di raggio unitario, oppure, in maniera analoga, una piastra finita con foro infinitesimo.
 Il caricamento a cui la piastra è soggetta può essere di due tipi:
Il caricamento a cui la piastra è soggetta può essere di due tipi:
- Locale se il foro è pressurizzato;
- A remoto se si applica una tensione molto distante dal foro.
Vogliamo risolvere quest'ultimo caso attraverso la teoria dell'elasticità, in cui la lastra risulta caricata nel seguente modo:
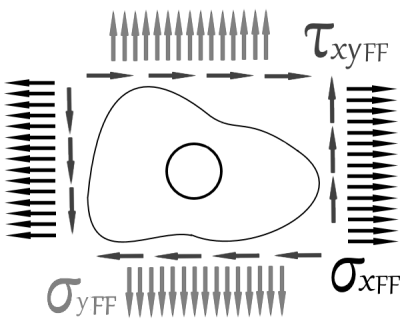
Per fare questo si devono risolvere 3 insiemi di equazioni:
- Equilibrio nel continuo
- Legame costitutivo
- Compatibilità cinematica
Equilibrio nel continuo
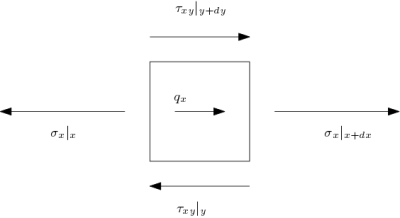
Facendo riferimento all'immagine 3, si considera un quadratino elementare infinitesimo di lati $dx$ e $dy$. Il quadratino è soggetto a tensioni in direzione $x$, che sono $\sigma_x|_x$ e $\sigma_x|_{x+dx}$. Sono presenti anche gli sforzi taglianti $\tau_{xy}|_y$, $\tau_{xy}|_{y+dy}$ e un carico distribuito di volume $q_x$. Facendo l'equilibrio in direzione $x$ si ottiene: \begin{equation}\label{1} q_x\, dx dy + dy\, ( \sigma_x|_{x+dx} - \sigma_x|_x) + dx\, (\tau_{xy}|_{y+dy}- \tau_{xy}|_y)=0 \end{equation} Per proseguire si ipotizza che le funzioni che descrivono le tensioni siano differenziabili, e a questo punto si sviluppa in serie di Taylor $\sigma_x|_{x+dx}$ e $\tau_{xy}|_{y+dy}$: \begin{align} \sigma_x|_{x+dx}= &\ \sigma_x|_x + \frac{\partial \sigma_x}{\partial x}\, dx + o(dx)\\ \tau_{xy}|_{y+dy}= &\ \tau_{xy}|_y + \frac{\partial \tau_{xy}}{\partial y}\, dy + o(dy) \end{align} Eliminando i termini di ordine superiore al primo, sostituendo all'equazione \ref{1}, e con un procedimento analogo per la direzione $y$, si ha: \begin{equation} \left\{ \begin{aligned} \frac{\partial \sigma_{x}}{\partial x} + \frac{\partial \tau_{xy}}{\partial y} = - q_x \\ \frac{\partial \sigma_{y}}{\partial y} + \frac{\partial \tau_{xy}}{\partial y} = - q_y \end{aligned} \right. \end{equation}
Legame costitutivo
Le equazioni del legame costitutivo sono: \begin{equation} \begin{bmatrix} \sigma_x\\ \sigma_y\\ \tau_{xy} \end{bmatrix} = \underline{\underline{D}} \begin{bmatrix} \epsilon_x\\ \epsilon_y\\ \gamma_{xy} \end{bmatrix} \end{equation}
Compatibilità cinematica
Le equazioni di compatibilità cinematica sono ($u$ è lo spostamento lungo $x$ e $v$ lungo $y$): \begin{align} \epsilon_x=&\ \frac{\partial u}{\partial x}\\ \epsilon_y=&\ \frac{\partial v}{\partial y}\\ \gamma_{xy}=&\ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \end{align}
Dalle equazioni dell'equilibrio nel continuo, del legame costitutivo e della compatibilità cinematica si ottengono 8 equazioni in 8 incognite: $\sigma_x$, $\sigma_y$, $\epsilon_x$, $\epsilon_y$, $\tau_{xy}$, $\gamma_{xy}$, $u$ e $v$. Per risolvere queste 8 equazioni si utilizzerà il testo di riferimento: J.R. Barber, Elasticity, da
Analisi delle condizioni al contorno
Condizioni al bordo interno
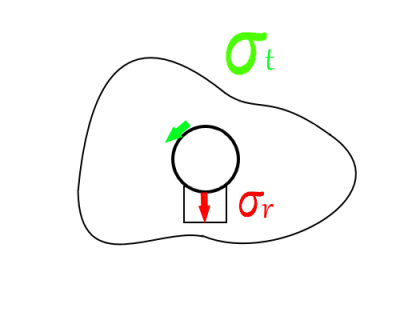
Nel caso in cui il foro fosse pressurizzato, in un elemento adiacente al foro si ha una $\sigma_r=-p$, dove $p$ è la pressione nel foro stesso. Nel nostro caso però la pressione non è presente e quindi $\sigma_r=0$. Dal momento in cui la faccia superficiale all'interno del foro deve essere scarica, non possono essere presenti neanche delle tensioni tangenziali $\tau_{rt}$ (Le tensioni circonferenziali $\sigma_t$ sono invece nonnulle). Per dare un significato fisico a queste condizioni si immagini un albero accoppiato con interferenza nel foro. La pressione di contatto che si sviluppa rappresenta la $\sigma_r$. Inoltre tale albero viene fatto ruotare nel foro. L'attrito presente genera una forza tangenziale che rappresenta $\tau_t$. Non essendo presente una pressurizzazione si può così immaginare che tali tensioni devono essere nulle.
Condizioni al bordo esterno
Il bordo esterno, in direzione $x$, è caricato da una $\sigma_{x_{ff}}$ (far field), il cui valore è definito come: \begin{equation} \sigma_{x_{ff}}=\lim_{r\to\infty} \sigma_x \end{equation} In maniera analoga, in direzione $y$ si ha: \begin{equation} \sigma_{y_{ff}}=\lim_{r\to\infty} \sigma_y \end{equation} e le forze tangenziali sono: \begin{equation} \tau_{{xy}_{ff}}=\lim_{r\to\infty} \tau_{{xy}_{ff}} \end{equation} Queste condizioni al contorno sono cartesiane e conviene passare alle condizioni polari. Per fare ciò consideriamo la figura
Il triangoli hanno ipotenusa di lunghezza unitaria e quindi i due cateti sono uno il coseno e l'altro il seno dell'angolo acuto $\theta$. Si procede facendo un equilibrio delle forze nella direzione della $\sigma_t$ (tangenziale) sul triangolo 1, ottenendo l'equazione eq. 1 trasl. (nella figura). Successivamente si farà un equilibrio delle forze agenti nella direzione di $\sigma_r$ sul triangolo 2 al fine di ottenere l'equazione eq. 2 trasl.. Per esprimere quindi la prima equazione si sono scomposte tutte le tensioni parallelamente e perpendicolarmente l'ipotenusa del triangolo 1. Per esempio $\sigma_x$ diventa, in direzione perpendicolare, $\sigma_x \sin \theta$, rappresentata di colore rosso. Questa componente di tensione moltiplicata per il segmento $\sin \theta$ sul quale è applicata rappresenta una delle forze in gioco. Considerando in questo modo tutte le tensioni si giunge alla prima equazione: \begin{align} \sigma_t=&\ \sin^2 \theta \sigma_x+ \cos^2 \theta \sigma_y-2 \cos \theta \sin \theta \tau_{xy}\\ \end{align} In maniera analoga si ottiene la seconda \begin{equation} \sigma_r= \cos^2 \theta \sigma_x+ \sin^2 \theta \sigma_y+2 \cos \theta \sin \theta \tau_{xy} \end{equation}
Nello scrivere le tensioni FarField nel sistema di riferimento polore si utilizza il codice fornito di Maxima: foglio ad inizio lezione
In questo programma viene utilizzato il comando “define(…)” per definire una funzione. Questo si differenzia dal comando“:=” solo per il fatto che il primo effettua una valutazione dell' argomento appena viene eseguito, nel secondo invece la valutazione dovrà essere effettuata in seguito. Per fare un esempio applicato al nostro caso si ha che “:=” non sostituisce la funzione “$\cos \theta$” al corrispettivo “c”, mentre “define(…)” si. Nel programma è usato anche il comando “trigreduce(…)” che altro non è che un manipolatore trigonometrico.
Soluzione al problema elastico
Si dimostra (vedi Jr. Barber, Elasticity, Pag 49) che è possibile ottenere l'andamento delle tensioni di un corpo elastico risolvendo l'equazione di Airy: \begin{equation} \nabla^4 \phi=0 \end{equation} Risolverla significa identificare una funzione che soddisfi le condizioni al contorno. Questa soluzione è una combinazione lineare di una serie di funzioni note, dette soluzioni di Mitchell. (vedi Jr. Barber, Elasticity, Pag 119)
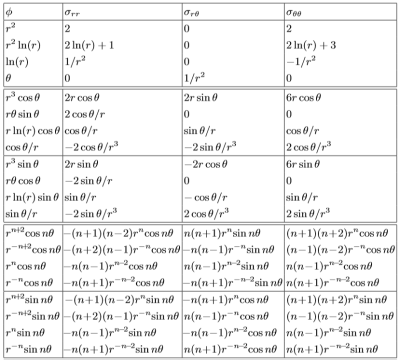
In questa tabella sono riportate le soluzioni plausibili $\phi$ e le relative espressioni di tensione radiale $\sigma_{rr}$, circonferenziale $\sigma_{\theta\theta}$ e $\sigma_{r\theta}$
A pagina 144 dello stesso Barber sono inoltre riportati gli andamenti delle deformazioni che si verificano con le medesime funzioni soluzione.
Di tutte queste funzioni solo alcune sono compatibili con le condizioni al contorno.
- La seconda funzione $\phi=r^2ln(r)$ dalla tabella a pag 133 ha un andamento della deformazione tangenziale $u_\theta$ lineare in $\theta$. Ciò implica un andamento non periodico della deformazione, non compatibile con la realtà in quanto a $\theta=0$ la deformazione tangenziale è nulla, ma a $\theta=2\pi$ assume un valere non nullo. Cosa impossibile essendo lo stesso punto della circonferenza. immagine spiegazione=== Dovrebbe essere considerata come soluzione nel controesempio in cui il foro è tagliato nel punto come in figura, in cui appunto si può avere discontinuità di deformazione. immagine controesempio===
- dalla $5^a$ alla $12^a$ soluzione abbiamo dei termini in $\theta$ mentre in maxima abbiamo manipolato le condizioni al contorno ottenendo termini in $2\theta$. Di conseguenza queste saranno scartate.
- Le soluzioni successive sono, per il motivo sopra espresso, accettabili solo con indice $n=2$. Delle stesse però la $13^a$ e la $17^a$ sono da escudere perchè presentano un termine in $r^2$ che non verifica la condizione al contorno per $r\rightarrow\infty$. Infatti: $$\sigma_r=r^2\rightarrow\infty\neq\cos(2\theta)$$
Concludendo sono rimaste nove funzioni che rispettano le condizioni al contorno. $\phi=$
- $r^2$
- $ln(r)$
- $\theta$
- $r^{-n+2}\cos\, {n\theta}$
- $r^{n}\cos\, {n\theta}$
- $r^{-n}\cos\, {n\theta}$
- $r^{-n+2}\sin\, {n\theta}$
- $r^{n}\sin\, {n\theta}$
- $r^{-n}\sin\, {n\theta}$
Queste saranno combinate linearmente e i coefficenti necessari saranno estrapolati mediante Maxima.
sezione Docente
- Elenco puntatoComponenti di tensione da definizione cartesiana a polare, per equilibrio.
testo di riferimento: J.R. Barber, Elasticity, da
Materiale corsi di NON libera distribuzione
Argomenti di riferimento:
- rotazione del sistema di riferimento per le componenti di tensione, p. 9 (27 pdf), da utilizzarsi nel passaggio da tensioni in coordinate cartesiane a tensioni in coordinate polari;
- operatore laplaciano e bilaplaciano, p. 49 (65 pdf) in coord. cartesiane, p. 111 (125 pdf) in coordinate polari;
- costante di Kolosov per tensione e deformazione piana, definizione delle comp. di deformazione p.43 (59 pdf);
- Airy stress function $\phi$, p. 46 (62 pdf);
- derivazione di $\sigma_{rr},\sigma_{\theta\theta},\tau_{r\theta}$ da $\phi$, p. 110 (124);
- termini della soluzione di Michell, componenti di tensione p. 119 (133);
- termini della soluzione di Michell, spostamenti p. 130 (144).