Indice
Richiami di teoria dell'elasticità
Introduzione alla teoria degli elementi finiti
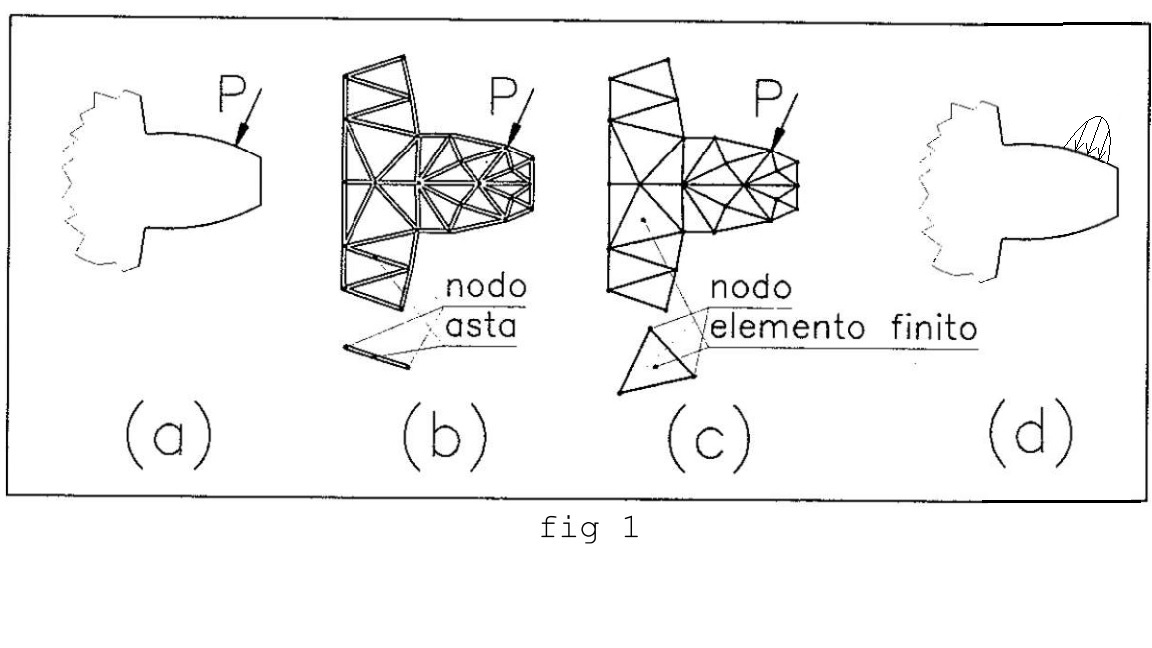
Il metodo degli elementi finiti viene applicato allo studio del comportamento di un componente meccanico, generalmente descritto da un sistema di equazioni differenziali: tramite una discretizzazione di tali equazioni, esse vengono trasformate in equazioni algebriche più semplici e in tal modo risolte in maniera approssimata. Un’applicazione di questo metodo è quello di verifica strutturale, ossia la determinazione di tensioni, deformazioni e spostamenti di ogni punto della struttura. Consideriamo un dettaglio di organo di macchina, per esempio un dente di ruota dentata, la cui connessione con il resto del componente è semplificata. Abbiamo quindi una porzione di elemento caricato per esempio con una forza concentrata P (come in figura 1a). Essa è una semplificazione: in un contatto tra due denti di due ruote che ingranano, si ha uno scambio di forze che avviene sulla piccola superficie di contatto, non in un punto solo, pertanto un caricamento più realistico sarebbe rappresentato da un carico distribuito di forma semi-ellittica, come in figura 1d. Analizziamo i fenomeni (stato tensionale in particolare) che avvengono localmente nel raccordo con il corpo della ruota scelto come punto d'interesse, tenendo conto che generalmente i punti critici da cui si innesca la rottura si trovano sulle superfici libere, salvo i casi di contatto hertziano e di superfici pressurizzate.
Il dente è schematizzato in 2D. Viene dunque definito un dominio elastico (al più elasto-plastico) continuo, cioè quella porzione di spazio occupata dal materiale costituente il dente, che si comporta secondo leggi elastiche nella deformazione. È possibile studiare il fenomeno tramite equazioni differenziali e le corrispondenti condizioni al contorno (cioè le condizioni che devono essere rispettate sul bordo del dominio considerato, in questo caso il dente). Esistono anche forze agenti dall’interno del dominio (ad esempio: forza di gravità, inerzia, ecc..): anch'esse vengono considerate condizioni al contorno. I carichi entrano nella struttura e in prossimità dello strappo.
La struttura così rappresentata non è in equilibrio, pertanto risulta necessario imporre dei vincoli.
In questo caso, per avere equilibrio agli spostamenti della struttura, si considera un incastro (in questo modo al dente viene come assegnata una posizione nello spazio): la scelta dell'incastro si giustifica considerando che il carico applicato P eserciti la sua influenza soltanto sul dente e nelle zone immediatamente vicine, ma non lontano dal dente stesso. I vincoli che impongono spostamenti nulli (come l'incastro dell'esempio) sono detti omogenei, viceversa non omogenei quelli che impongono spostamenti non nulli.
Anziché risolvere le equazioni differenziali che derivano dall'analisi della struttura, che sarebbe molto complesso, si può decidere di discretizzare il dominio in elementi di volume finito.
In passato, il tentativo di considerare il problema come se fosse costituito da aste e nodi in cui esse si collegano tra loro (figura 1b) non ha dato risultati sufficientemente precisi, in quanto non considerava la presenza di materiale tra le aste e pertanto sottostimava la rigidezza totale.
Stabilisco un sistema di assi cartesiani comodo per la zona del raccordo che sto considerando, cioè formato da una terna di assi tali che uno sia normale alla superficie del dente con verso uscente (n) e due tangenti alla superficie (parallelo t e perpendicolare w) al piano del disegno 2D.
Definiamo convenzionalmente gli spostamenti:
- “u” sono gli spostamenti in direzione x
- “v” sono gli spostamenti in direzione y
- “w” sono gli spostamenti in direzione z
Con piani normali agli assi cartesiani appena definiti, ritaglio un intorno di materiale in corrispondenza del raccordo: questo sarà il cubetto di materiale di riferimento. Vogliamo stabilire lo stato tensionale del cubetto.
Equazioni di equilibrio nel continuo
Per la trattazione di un corpo continuo si procede analizzando una porzione infinitesima di materiale, considerata per semplicità di forma cubica. Il cubetto sarà caratterizzato da un suo stato tensionale, che dipende ovviamente da quello globale dell’elemento considerato (in questo caso il dente). Lo stato tensionale è rappresentabile, una volta definito il sistema di assi cartesiani xyz, tramite le componenti (normali e tangenziali) di tensione che agiscono sulle facce del cubetto infinitesimo.
Si distinguono tensioni normali, σ, e tangenziali, τ, le prime agenti perpendicolarmente alla faccia del cubetto elementare; le seconde parallelamente. La Figura presenta le tensioni sulle facce del cubetto: per ogni faccia, esiste una tensione normale e due tangenziali.
Le tensioni σ sono dimensionalmente una forza su un'area F/A: useremo pertanto come unità di misura il [MPa] = [N/mm^2]. Sul cubetto possono essere presenti fino a 3 componenti di tensione σ, una per ogni direzione cartesiana. Per l'equilibrio del cubetto sarà necessario, in assenza di forze di campo e a meno di incrementi infinitesimi, che ognuna di esse sia equilibrata da una tensione σ uguale e opposta sulla faccia opposta del cubetto, per garantire l'equilibrio alla traslazione.
Per quanto riguarda le tensioni τ, osserviamo il cubetto ortogonalmente a una delle sue facce (figura 3): questa è caratterizzata da un asse cartesiano ad essa perpendicolare (l'asse z, nel caso della faccia mostrata in figura 3): il nome di tale asse (qui z) è dunque anche utilizzato come nome della faccia in questione. Si può notare come le tensioni agenti sulle facce collegate (non visibili in figura) seguano un andamento particolare. Data una tensione τ, di valore incognito e verso arbitrario (in questo caso destra) sulla faccia superiore, per equilibrio alla traslazione deve esisterne una uguale in modulo e opposta in verso sulla faccia opposta (inferiore); tuttavia, per non violare l'equilibrio alla rotazione, è necessario anche che sulle due restanti facce esista una coppia di tensioni, ancora di uguale modulo e con verso tale da collegarsi punta-punta e coda-coda con le altre due. Le componenti di τ vengono identificate con due pedici: il primo corrispondente alla faccia su cui le vado a considerare (secondo la convenzione prima definita per assegnare il nome a una faccia del cubetto) e il secondo con la direzione cartesiana su cui agisce. Considerando di applicare lo stesso ragionamento alle altre viste del cubetto, nel complesso si ha che in ogni cubetto infinitesimo esistono 3 tensioni σ e 3 tensioni τ effettivamente indipendenti tra loro, per un totale di 6 incognite per poter definire univocamente lo stato tensionale del cubetto.
$$ \begin{cases} & \tau_{xy} = \tau_{yx}\\ &\tau_ {xz}=\tau_ {zx}\\ &\tau_ {yz}=\tau_ {zy} \end{cases} $$
Il caso in cui una faccia del cubetto elementare sia appartenente alla superficie libera (cioè interfaccia con l'aria) è un particolare caso in cui alcune delle componenti tensionali prima descritte sono nulle. In particolare non possono esistere tensioni di nessun tipo su tale superficie: queste non potrebbero infatti essere equilibrate da nessuna altra tensione, a meno che l'ambiente in cui si trova il componente non sia in pressione. Essendo nulle quelle tensioni, sono nulle anche quelle corrispondenti ad esse sulle altre facce. Quindi 3 componenti di tensione su 6 sono nulle: $\sigma _{n}$, $\tau _{nt}$, $\tau _{nw}$ (dove n,t,w sono i tre assi della terna cartesiana nello spazio, ben orientata rispetto al cubetto elementare). Mentre risulta possibile attribuire una fisicità al segno della tensione σ (positiva se di trazione, cioè uscente dalla faccia del cubetto, negativa se di compressione: è una convenzione opposta a quella delle pressioni), non è possibile dare un segno fisico alla τ.
Segno della τ in problemi di teoria dell'elasticità
Tale convenzione viene impiegata nello studio di problemi strettamente connessi con le equazioni differenziali di equilibrio delle tensioni: se la normale uscente alla faccia del cubetto è equiversa all'asse cartesiano x, y, z, a cui è parallela, allora la tensione τ è positiva se orientata secondo la direzione positiva dell'asse a cui è parallela. Se invece la normale uscente alla faccia del cubetto è controversa con l'asse cartesiano x, y, z, a cui è parallela, allora la tensione τ è positiva se controversa con l'asse a cui è parallela.
Per esempio in Figura la tensione τ è negativa perché, mentre σ (rappresentata positiva, e quindi facente le veci della normale uscente) è equiversa con l'asse x (l'asse a cui σ è parallela), τ è controversa con l'asse y (l'asse a cui τ è parallela).
Equazioni di equilibrio alla traslazione
Le equazioni di equilibrio alla traslazione sono, in assenza di forze di massa:
$$ \frac{ \partial \sigma_x }{ \partial x } + \frac{ \partial \tau_{xy} }{ \partial y } + \frac{ \partial \tau_{zx} }{ \partial z } =0 $$
$$ \frac{ \partial \tau_{xy} }{ \partial x } + \frac{ \partial \sigma_y }{ \partial y } + \frac{ \partial \tau_{yz} }{ \partial z } =0 $$
$$ \frac{ \partial \tau_{zx} }{ \partial x } + \frac{ \partial \tau_{yz} }{ \partial y } + \frac{ \partial \sigma_z }{ \partial z } =0 $$
Equazioni di compatibilità cinematica
Consideriamo adesso le equazioni di compatibilità cinematica, che imporranno l’assenza di “strappi” nel materiale. Queste devono essere scritte in funzione degli spostamenti, in modo da rispettare le equazioni di continuità. Posti u, v, w rispettivamente gli spostamenti lungo x, y e z si ottiene:
$$ \begin{cases} \epsilon_{x}=\frac{\partial u}{\partial x},\\ \epsilon_{y}=\frac{\partial v}{\partial y},\\ \epsilon_{z}=\frac{\partial w}{\partial z},\\ \gamma_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y},\\ \gamma_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z},\\ \gamma_{zx}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x},\\ \end{cases} $$
u, v, w sono funzioni continue sul dominio elastico. Scrivendo la relazione tra le deformazioni e gli spostamenti, si limitano i possibili stati deformativi a quelli che rispettano la compatibilità.
Equazioni di legame costitutivo
Dobbiamo infine trovare un legame tra tensioni σ e deformazioni ε che, se il materiale è isotropo, risulta di tipo lineare e segue la legge di Hooke:
$$ \sigma _{x}=\frac{\nu E}{\left ( 1+\nu \right )\left ( 1-2\nu \right )}\left ( \varepsilon _{x} +\varepsilon _{y}+\varepsilon _{z}\right )+\frac{E}{1+\nu }\varepsilon _{x} \\ \sigma _{y}=\frac{\nu E}{\left ( 1+\nu \right )\left ( 1-2\nu \right )}\left ( \varepsilon _{x} +\varepsilon _{y}+\varepsilon _{z}\right )+\frac{E}{1+\nu }\varepsilon _{y} \\ \sigma _{z}=\frac{\nu E}{\left ( 1+\nu \right )\left ( 1-2\nu \right )}\left ( \varepsilon _{x} +\varepsilon _{y}+\varepsilon _{z}\right )+\frac{E}{1+\nu }\varepsilon _{z} $$
Si può anche dire che il vettore delle tensioni agenti è uguale al vettore delle deformazioni premoltiplicato per la matrice di legame elastico
$$ \def\X{\frac{E\left(1-\nu\right)}{\left(1-2\nu\right)\left(1+\nu\right)}} \def\Y{\frac{E\nu }{\left(1-2\nu\right)\left(1+\nu\right)}} \begin{bmatrix} \sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} = \begin{bmatrix} \X&\Y&\Y&0&0&0 \\ \Y&\X&\Y&0&0&0 \\ \Y&\Y&\X&0&0&0 \\ 0 &0 &0 &G&0&0 \\ 0 &0 &0 &0&G&0 \\ 0 &0 &0 &0&0&G \end{bmatrix} \begin{bmatrix} \epsilon_{x}\\ \epsilon_{y}\\ \epsilon_{z}\\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} $$
È possibile scrivere anche l’operazione inversa, premoltiplicando il vettore delle tensioni per l’inversa della matrice di legame elastico, ottenendo così il vettore delle deformazioni. Gli zeri presenti in entrambe le matrici indicano l’assenza di legami tra le σ e le γ e tra le τ e le ε .
$$ \def\X{\frac{1} {E}} \def\Y{\frac{-\nu}{E}} \def\Z{\frac{1} {G}} \begin{bmatrix} \epsilon_{x}\\ \epsilon_{y}\\ \epsilon_{z}\\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{bmatrix} = \begin{bmatrix} \X&\Y&\Y&0&0&0 \\ \Y&\X&\Y&0&0&0 \\ \Y&\Y&\X&0&0&0 \\ 0 &0 &0 &\Z&0&0 \\ 0 &0 &0 &0&\Z&0 \\ 0 &0 &0 &0&0&\Z \end{bmatrix} \begin{bmatrix} \sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{bmatrix} $$
Si ottengono quindi le seguenti equazioni:
$$ \epsilon _{x}=\frac{1}{E}\left [ \sigma _{x}-\nu \left ( \sigma _{y}+\sigma _{z} \right ) \right ] \\ \epsilon _{y}=\frac{1}{E}\left [ \sigma _{y}-\nu \left ( \sigma _{x}+\sigma _{z} \right ) \right ] \\ \epsilon _{z}=\frac{1}{E}\left [ \sigma _{z}-\nu \left ( \sigma _{x}+\sigma _{y} \right ) \right ] \\ \gamma _{xy}=\frac{1}{G}\tau _{xy} \\ \gamma _{yz}=\frac{1}{G}\tau _{yz} \\ \gamma _{zx}=\frac{1}{G}\tau _{zx} $$
Queste equazioni, dette di legame costitutivo, valgono per piccole deformazioni (riscontrabili in tutti i materiali metallici, come l’acciaio, e in parte dei materiali polimerici non gommosi) e sotto l'ipotesi di materiali elastici, lineari, omogenei, isotropi.
Si noti che:
- E rappresenta il modulo di Young,
- $\nu$ rappresenta il coefficiente di Poisson (per i materiali di nostro interesse, principalmente metallici, vale circa 0,3)
- G rappresenta il modulo di taglio, legato a E e $\nu$ dalla relazione:
$$ G=\frac{E}{2\left ( 1+\nu \right )} $$
Il problema che ci poniamo è quello di analizzare lo stato tensionale in tutti i punti critici della struttura, cioè determinare in tali punti le tensioni, le deformazioni e gli spostamenti. Si hanno 6 componenti di tensione, 6 componenti di deformazione e 3 componenti di spostamento, cioè ci sono, teoricamente, 15 incognite in ogni punto. In realtà queste 15 incognite non sono indipendenti, utilizzando infatti le leggi viste è possibile derivare dagli spostamenti tutte le altre incognite.