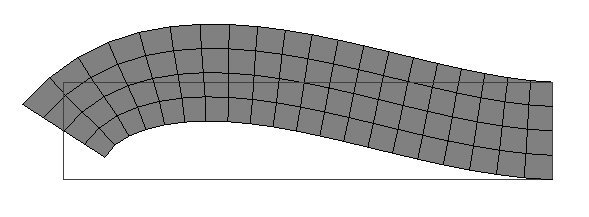
Partiamo dallo studio dell'elemento trave di cui la piastra ne è l'estensione.

Assegnata una trave in 2 dimensioni, è caratterizzata da spostamenti nelle direzioni “X” e “Z” chiamate rispettivamente “U₁” e “W₁” associate al nodo 1; mentre “U₂” e “W₂” relativamente al nodo 2; si hanno inoltre due rotazioni φ₁ e φ₂ relativamente ai nodi “1” e “2”.

Nel caso di trave in tre dimensioni si hanno 12 g.d.l rispettivamente tre spostamenti e tre rotazioni per nodo.

Estendendo il nodo in tre dimensioni sopra riportato, si vanno a valutare le rototraslazioni delle sezioni.

Nel caso di Torsione, la conservazione delle sezioni piane si ha solo per cilindri e cilindri cavi dunque è più complicato trattarla.

Consideriamo i casi di trave che lavora con carichi:

• Flessionali: Trave sottile nella quale è trascurabile la deformazione a taglio detta anche trave di Eulero-Bernoulli;
• Flesso-Taglianti: Trave spessa o trave alla “Timoshenko” nella quale l'effetto della deformazione a taglio non è trascurabile ;
• A sforzo normale.

In teoria si parla di trave sottile quando il rapporto tra la dimensione caratteristica della sezione (spessore “S”) e del corpo (lunghezza della trave “L”) è maggiore di 1:10. Nella pratica il valore di questo rapporto può variare in base all'errore che si vuole ottenere (es: se L = 10 S allora commettiamo un errore di circa 10%) in genere più questo rapporto è piccolo, più l'errore sarà esiguo.

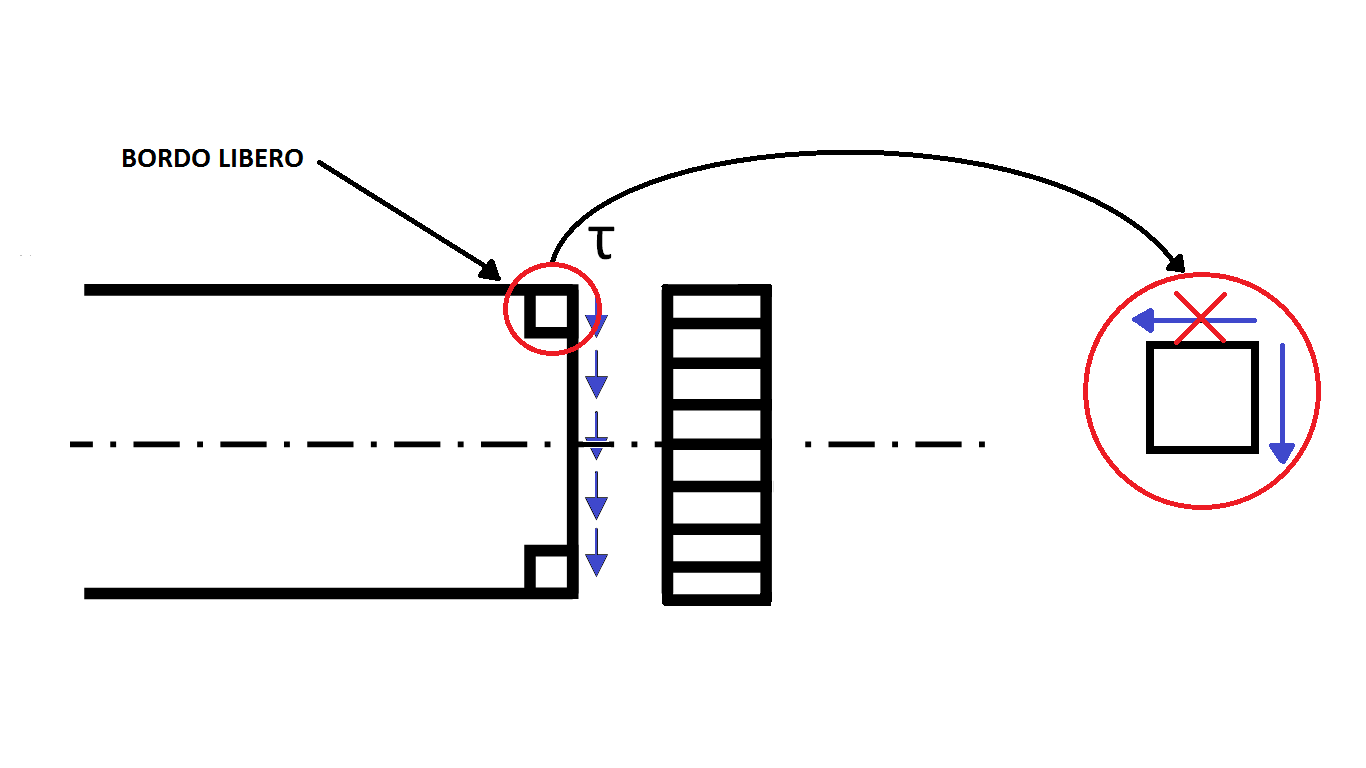
Ipotizzando una distribuzione costante delle “τ” avrei una situazione impossibile sul bordo della trave in quanto la “τ” non sarebbe equilibrata visto che la parte superiore della trave è a contatto con l'aria.

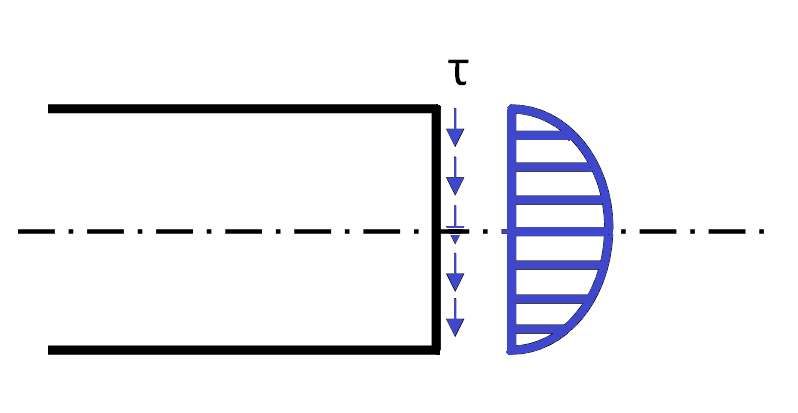
Dunque si deduce che ho un andamento parabolico da “0” a “τ_MAX” con “τ_MAX = 1.5 T/A”

Per calcolare l'energia potenziale dell'elemento di trave piena impongo una compressione sulla trave: u₁=1 e u₂=v₁=..=0 La sezione è lasciata libera di deformarsi sotto l'effetto Poisson

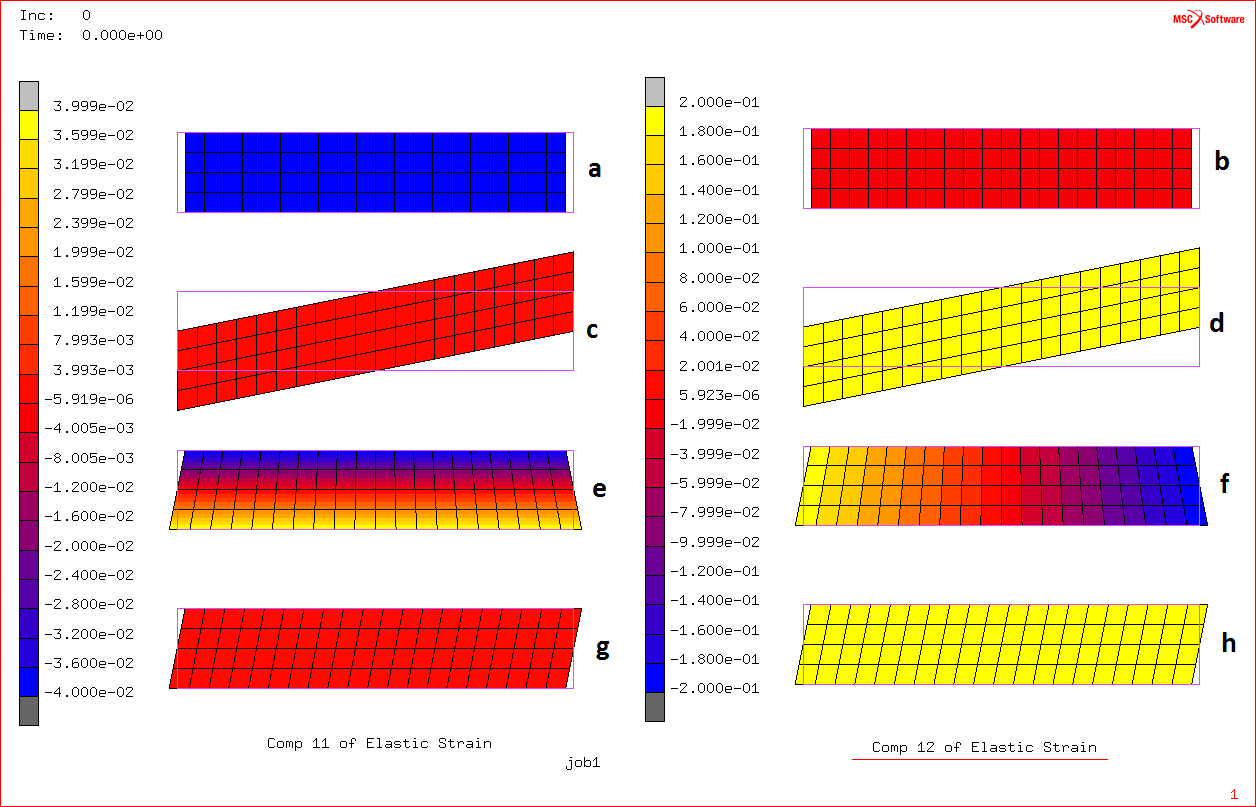
In riferimento all' immagine riportata di sotto abbiamo 4 funzioni di forma :

• Trazione
• Compressione
• Taglio
• Flessione

Per quanto riguarda il taglio si verifica solo quando w₁ ≠ 0 (o w₂≠0 nell'altro caso). In questo caso siamo in presenza di un problema cubico, servono quattro costanti w₁, w₂, φ₁, φ₂. L'espressione della deformata è:

ω(ξ)=a(ξ³)+ b(ξ²) + c(ξ) + d

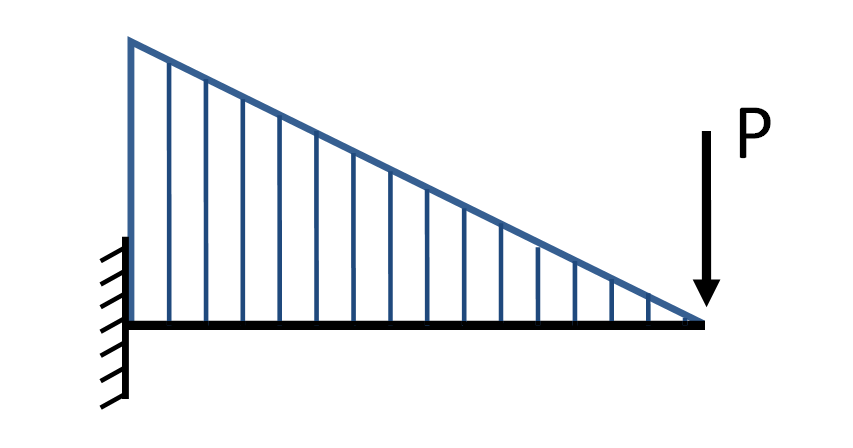
Considerando un esempio semplice di trave puramente soggetta a flessione con carico concentrato all'estremità libera si ha che spostamenti e rotazioni non sono disgiunti. Il momento flettente risulta essere lineare, la curvatura è lineare e quindi la deformata ω è cubica

Imponendo una rotazione di un radiante all'estremità libera della trave anche qui la deformata è un espressione cubica che consente di ricavare l'andamento di Mf. Ciò che manca rispetto al caso 2D rispetto al 3D sono i due moti torsionali rispetto ai nodi (3D=12 g.d.l.) I risultati ottenuti dalla teoria di Bernoulli sono interpretati nella teoria di Timoshenko nel seguente modo: considerando la trave che si “deforma ad S” spostamenti e deformazioni possono essere disaccoppiati in 2 spostamenti nodali oppure uno spostamento nodale sommato ad una traslazione rigida. Tale deformata ottenuta dalla trave di Eulero nel caso di flessione pura può essere interpretata secondo la teoria di Timoshenko come le figure c e g che rappresentano lo stesso tipo di sollecitazione a taglio a meno di una rotazione.

In letteratura si hanno due formulazioni riguardo la trave:

• * Si definisce una legge per la rototraslazione di ogni punto sull'asse della trave,quindi dalle rototraslazioni dei due nodi (sia nel caso 2d che nel caso 3d) vengono derivati spostamenti e rotazioni di ogni punto sull'asse della trave, cui ovviamente corrisponde viene una sezione. Andando a considerare l'evoluzione delle rototraslazioni delle sezioni di tipo deformativo si vanno a calcolare le deformazioni flessionali, di sforzo normale e torsionale. È immediato andare a vedere le deformazioni flessionali, taglianti e sforzo normale, costruite partendo dall'ipotesi di conservazione delle sezioni piane; un pò più complicato è andare a definire la torsione, perchè la torsione conserva le sezioni piane solo per cilindri cavi o pieni. Per l'elemento trave conosciamo due formulazioni: tipicamente si parla di travi flessionali e travi flessotaglianti (più eventualmente lo sforzo normale, che però è più facilmente gestibile). Per quanto riguarda la prima formulazione, si parla di travi flessionali per travi che non deformano a taglio, ma solo a flessione. Solitamente vengono associate alla trave di Eulero-Bernoulli. Si può parlare anche di trave sottile, nel senso che la deformazione a taglio è trascurabile quando la grandezza caratteristica della sezione è molto più piccola della lunghezza non dell'elemento ma della struttura (storicamente si parla di rapporti 1:10). È stata formulata anche una teoria per la trave flessotagliante, detta anche trave spessa, che viene tipicamente indicata come trave di Timoshenko, e che si trova a gestire una componente tagliante che però, per ipotesi, è uniforme sulla sezione: come sappiamo, su una sezione rettangolare il taglio ha andamento parabolico, ma quello che si fa è andare a considerare un taglio medio. Perchè in una sezione rettangolare soggetta a taglio le azioni taglianti non possono avere andamento costante? Perchè se supponessimo fosse costante, andremmo incontro a due paradossi fisici: estrapolando i due quadratini evidenziati in figura, avrei uno stato tensionale che vede una trave non scarica su due facce che però si equilibrano complessivamente, mentre non può esistere una TAU su “questa” faccia perchè è un bordo libero. Questa distribuzione dunque non può essere, per cui ho una distribuzione di tipo parabolico, che correttamente, in corrispondenza degli estremi, ha TAU nulla. Vediamo cosa succede se considero una trave piana con le funzioni di forma associate. Sono rappresentate le possibili funzioni di forma. Vedete le sei funzioni di forma associate ai sei gradi di libertà: la prima è una traslazione unitaria in direzione x. u1=0 e tutti gli altri nulli. La trave in questo caso si comprime.

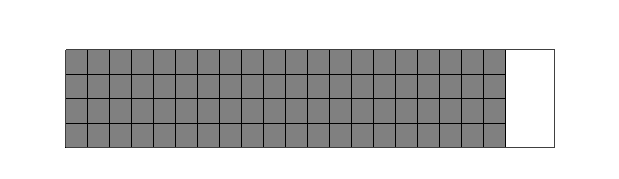
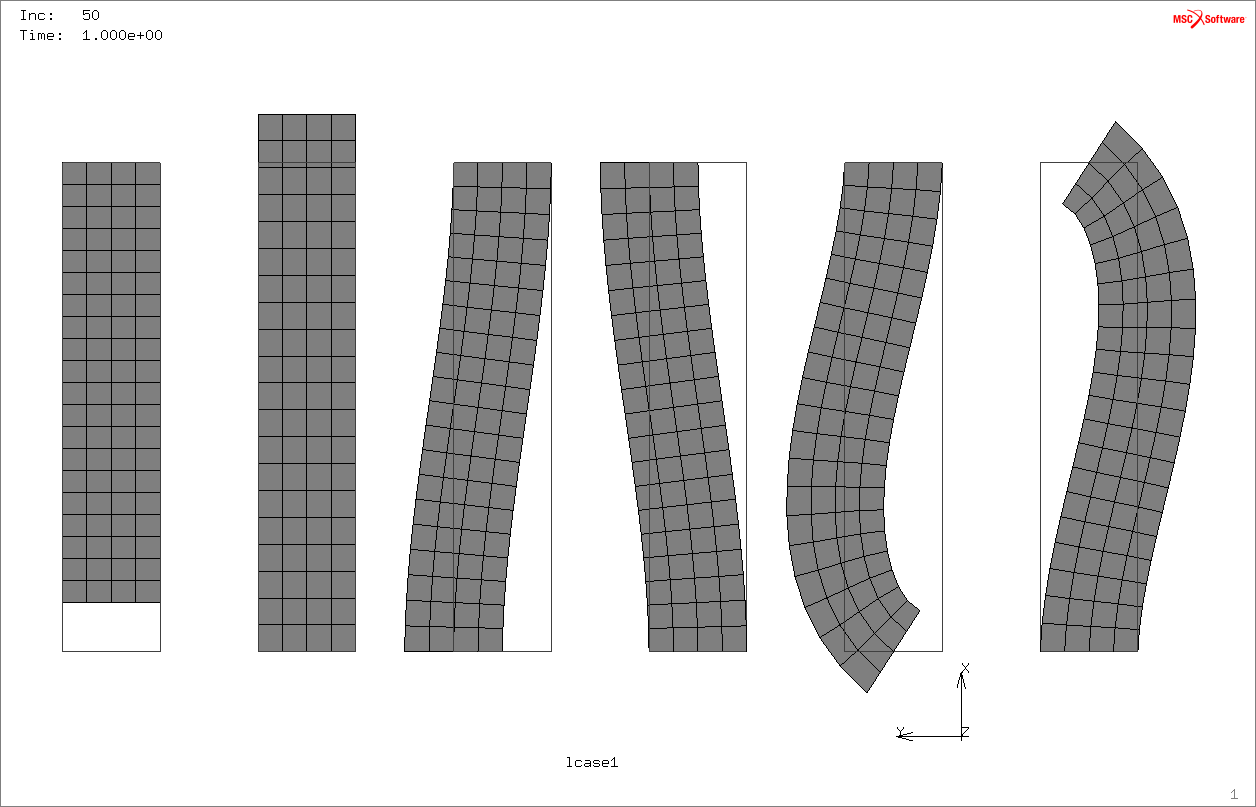
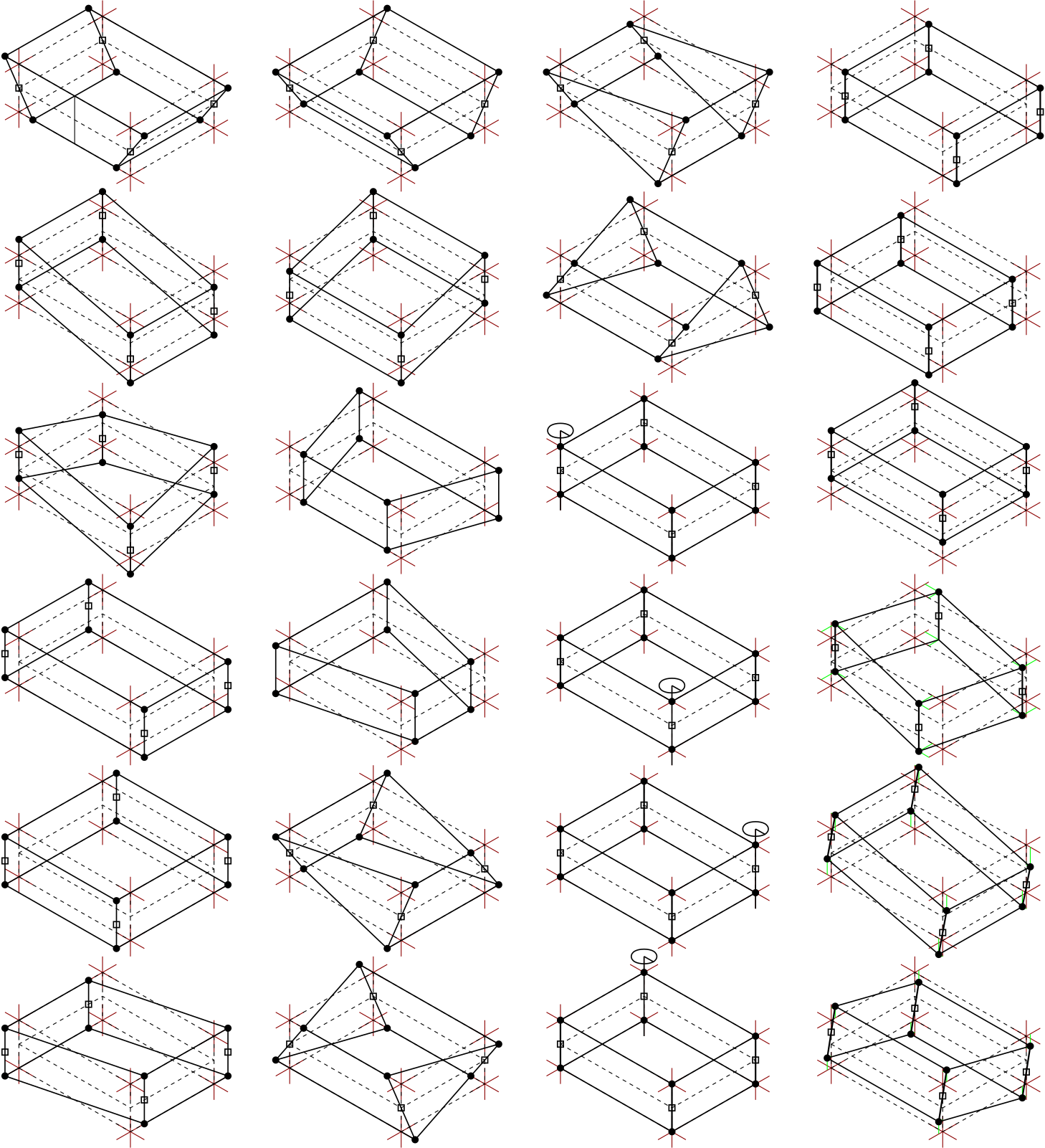
Trave flessionale: funzioni di forma

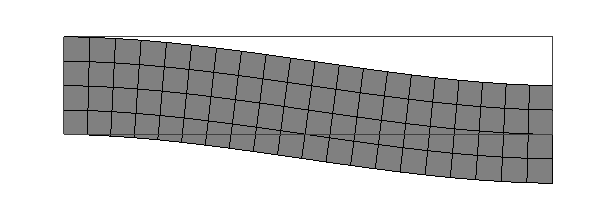
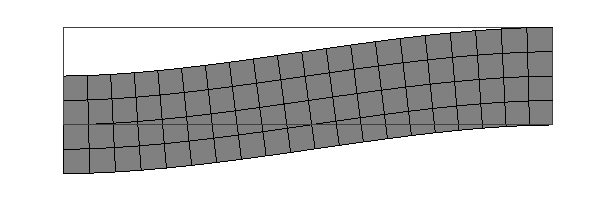
Trave flessotagliante (Timoshenko beam)

Notare shear locking se non sottointegrato.

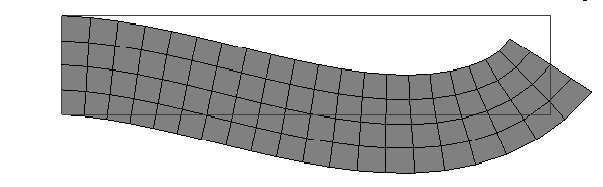
Piastra flessotagliante (Mindlin plate, ele95 Marc)

4

immagini varie

=======**in fase di stesura**======